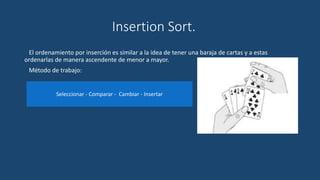
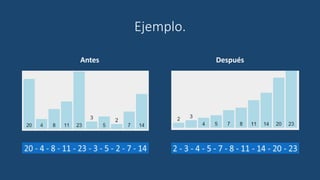
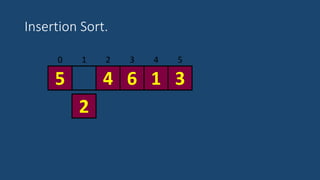
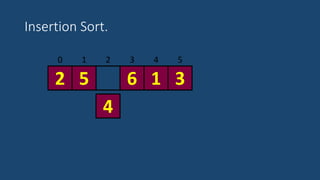
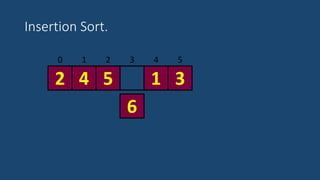
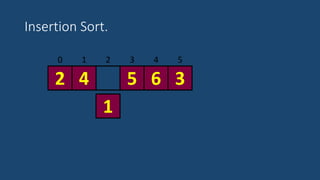
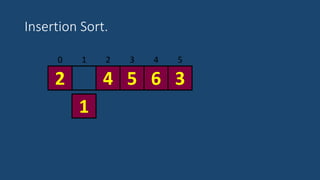
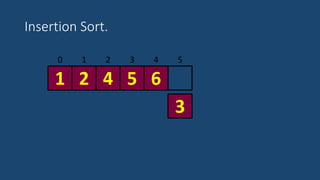
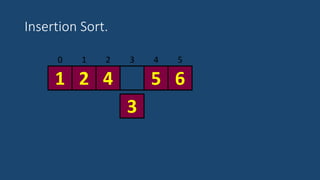
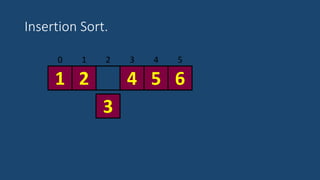
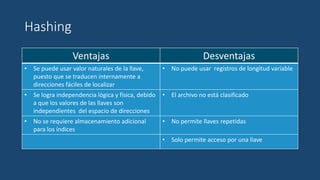
El documento describe el algoritmo de ordenamiento por inserción. Funciona insertando elementos uno por uno en una lista ordenada. Compara cada nuevo elemento con los elementos anteriores y los mueve hacia atrás si es necesario para insertarlo en la posición correcta. El proceso se repite hasta que la lista esté completamente ordenada.

1. Insertion Sort
Michael Toledo

2. Insertion Sort.
El ordenamiento por inserción es similar a la idea de tener una baraja de cartas y a estas
ordenarlas de manera ascendente de menor a mayor.
Método de trabajo:
Seleccionar - Comparar - Cambiar - Insertar

3. Insertion Sort
Ventajas Desventajas
• Simple. • Es deficiente en grandes listas.
• Fácil de usar. • En algunos casos es lento.
• Requerimiento mínimo de memoria. • Realiza numerosas comparaciones.
• Eficiente en listas pequeñas. • No funciona tan bien como otros algoritmos
de ordenamiento.

4. Ordenamiento por inserción.
¿Como funciona?
Este método funciona de la siguiente manera, toma cada elemento del arreglo y lo compara con
elementos que se encuentran en posiciones anteriores. Si resulta que el elemento con el que se
está comparando es mayor que el elemento a ordenar, estos se intercambian de posición. Si por el
contrario, resulta que el elemento con el que se está comparando es menor que el elemento a
ordenar, se detiene el proceso de comparación pues, se encontró que el elemento ya está ordenado
y se coloca en su posición . A continuación, ejemplo de una lista de 10 elemento.
20 - 4 - 8 - 11 - 23 - 3 - 5 - 2 - 7 - 14

5. Ejemplo.
1° paso: En un método de ordenamiento por inserción, la comparación se hará desde el segundo
elemento de la lista al cual llamaremos i, a continuación se verificara que i sea menor a su
antecesor, de ser verdad esta afirmación, i se intercambiara con su antecesor; de lo contrario, si la
afirmación es falsa, el 2° elemento no se moverá si no que tomara la posición de su sucesor,
sabiendo que el 2° elemento ya esta ordenado.
Quedando de esta manera:
20 - 4 - 8 - 11 - 23 - 3 - 5 - 2 - 7 - 14
iAntecesor
4 - 20- 8 - 11 - 23 - 3 - 5 - 2 - 7 - 14
Sucesor

6. Ejemplo.
2° paso: i tomará la posición de 8, y este se comparara con 20, 8 < 20 es verdadero, se intercambian
entre si.
Quedando de esta manera:
A continuación se compara 8 < 4 es falso, 8 no se moverá por que este se encuentra ordenado.
4 - 20 - 8 - 11 - 23 - 3 - 5 - 2 - 7 - 14
Anterior i
4 - 8 - 20 - 11 - 23 - 3 - 5 - 2 - 7 - 14

7. Ejemplo.
3° paso: i tomará la posición de 11, y se comparara 11 < 20 es verdadero, se intercambiara entre si.
Quedando de esta manera:
A continuación se comparara 11 < 8 & 11 < 4, lo cual es falso y 11 no se moverá dado que ya se
encuentra ordenado.
4 - 8 - 20 - 11 - 23 - 3 - 5 - 2 - 7 - 14
i
4 - 8 - 11 - 20 - 23 - 3 - 5 - 2 - 7 - 14

8. Ejemplo.
4° paso: i tomará la posición de 23, y se comparara 23 < 20 es falso, no se moverá por que ya se
encuentra en orden.
5° paso: i tomará la posición de 3, y se comparara 3 < 23 & 3 < 20… hasta llegar a 3 < 4, todas estas
comparaciones van a ser verdaderas y se intercambiaran entre si, quedando el 3 en la primera
posición.
A continuación quedara de la siguiente forma:
4 - 8 - 11 - 20 - 23 - 3 - 5 - 2 - 7 - 14
4 - 8 - 11 - 20 - 23 - 3 - 5 - 2 - 7 - 14
i
3 - 4 - 8 - 11 - 20 - 23 - 5 - 2 - 7 - 14

9. Ejemplo.
6° paso: i tomará la posición de 5, y se comparara 5 < 23 & 5 < 20… hasta llegar a 5 < 8, todas estas
afirmaciones serán verdaderas.
Una vez llegue a 5 < 4 esto va a ser falso, por lo tanto 5 quedara antes de 8 y después de 4,
quedando de esta manera:
3 - 4 - 8 - 11 - 20 - 23 - 5 - 2 - 7 - 14
i
3 - 4 - 5 - 8 - 11 - 20 - 23 - 2 - 7 - 14

10. Ejemplo.
7° paso: i tomará la posición de 2, este se comparara, 2 < 23 & 2 < 20… hasta llegar a 2 < 3, todas
estas afirmaciones serán verdaderas, y 2 quedara en la primera posición.
De esta forma:
i
3 - 4 - 5 - 8 - 11 - 20 - 23 - 2 - 7 - 14
2 - 3 - 4 - 5 - 8 - 11 - 20 - 23 - 7 - 14

11. Ejemplo.
8° paso: i tomará la posición de 7, este se comparara 7 < 23 & 7 < 20… hasta llegar a 7 < 8, todas
estas afirmaciones serán verdaderas, 7 < 5 es falso por lo tanto 7 quedara antes de 8 y después de
5.
Quedando de esta manera:
i
2 - 3 - 4 - 5 - 8 - 11 - 20 - 23 - 7 - 14
2 - 3 - 4 - 5 - 7 - 8 - 11 - 20 - 23 - 14

12. Ejemplo.
9° paso: i tomará la posición de 14, este se comparara 14 < 23 & 14 < 20, estas afirmaciones serán
verdaderas, 14 < 11 es falso por lo tanto 14 quedara antes de 20 y después de 11.
Quedando de esta manera:
i
2 - 3 - 4 - 5 - 7 - 8 - 11 - 20 - 23 - 14
2 - 3 - 4 - 5 - 7 - 8 - 11 - 14 - 20 - 23

13. Ejemplo.
Antes Después

14. Insertion Sort.
3 4 50 1 2
5 2 4 6 1 3

15. Insertion Sort.
3 4 50 1 2
5
2
4 6 1 3

16. Insertion Sort.
3 4 50 1 2
2
5 4 6 1 3

17. Insertion Sort.
3 4 50 1 2
52 4 6 1 3

18. Insertion Sort.
3 4 50 1 2
52
4
6 1 3

19. Insertion Sort.
3 4 50 1 2
52
4
6 1 3

20. Insertion Sort.
3 4 50 1 2
52 4 6 1 3

21. Insertion Sort.
3 4 50 1 2
52 4
6
1 3

22. Insertion Sort.
3 4 50 1 2
52 4 6 1 3

23. Insertion Sort.
3 4 50 1 2
52 4 6
1
3

24. Insertion Sort.
3 4 50 1 2
52 4 6
1
3

25. Insertion Sort.
3 4 50 1 2
52 4 6
1
3

26. Insertion Sort.
3 4 50 1 2
52 4 6
1
3

27. Insertion Sort.
3 4 50 1 2
52 4 6
1
3

28. Insertion Sort.
3 4 50 1 2
52 4 61 3

29. Insertion Sort.
3 4 50 1 2
52 4 61
3

30. Insertion Sort.
3 4 50 1 2
52 4 61
3

31. Insertion Sort.
3 4 50 1 2
52 4 61
3

32. Insertion Sort.
3 4 50 1 2
52 4 61
3

33. Insertion Sort.
3 4 50 1 2
52 4 61 3

34. Hashing
¿Cómo funciona?
Es un método de búsqueda que consiste en aplicar una función que traduce un
conjunto de posibles valores (llave) en un rango de direcciones relativas en una
estructura de datos dinámica o estática.

35. Hashing
Ventajas Desventajas
• Se puede usar valor naturales de la llave,
puesto que se traducen internamente a
direcciones fáciles de localizar
• No puede usar registros de longitud variable
• Se logra independencia lógica y física, debido
a que los valores de las llaves son
independientes del espacio de direcciones
• El archivo no está clasificado
• No se requiere almacenamiento adicional
para los índices
• No permite llaves repetidas
• Solo permite acceso por una llave