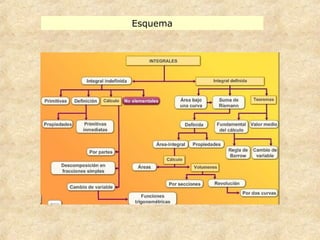
Este documento presenta los conceptos fundamentales de las integrales indefinidas y sus propiedades. Explica cómo calcular integrales inmediatas mediante tablas de derivadas y el uso de la integración por partes, sustitución y descomposición en fracciones simples para integrales más complejas. Proporciona ejemplos detallados de cada método.

1. Presentación elaborada por la profesora Ana Mª Zapatero a partir
de los materiales utilizados en el centro (Editorial SM)
Integrales indefinidas. Teoremas
2º Bachillerato

2. Esquema

3. Primitiva de una función
La función G(x) es una primitiva de la función f(x) en un intervalo I
si G'(x) = f(x) para todo x del intervalo I.
Ejemplo: la función F(x) =
x4
4 es una primitiva de f(x) ya que F '(x) = x3
.
También la función G(x) =
x4
4
+ 2 es una primitiva de f . Ambas en
cualquier intervalo de la recta real.

4. Integral indefinida
Ejemplo: la integral indefinida de f(x) = ex
es G(x) = ex
+ C, donde C es una cons-
tante. Se expresa de la siguiente manera: ⌡⌠ ex
dx = ex
+ C
Si G(x) es una primitiva de f(x) en un intervalo I, todas las primitivas de f(x) son
de la forma G(x) + C, donde C es una constante arbitraria que puede ser
cualquier número real.

5. Las primitivas se diferencian en una constante
Integrando
↓↑Derivando

6. Propiedades de la integral indefinida
I ⌡
⌠ k f(x) dx = k ⌡
⌠ f(x) dx con k ∈ R
Las constantes pueden salir y entrar fuera del
signo de la integral indefinida.
II ⌡
⌠
[ f(x) ± g(x)] dx = ⌡
⌠ f(x) dx ±⌡
⌠ g(x) dx
La integral indefinida de una suma (resta) de
dos funciones es la suma (resta) de las inte-
grales indefinidas.
Propiedades de la integral indefinida
Propiedades de la derivada
I (kf )' (x) = k f '(x) con k ∈ R
La derivada de una constante por una
función es el producto de la constante
por la derivada de la función.
II (f ± g) ' (x) = f ' (x) ± g ' (x)
La derivada de una suma (resta) de dos
funciones es la suma (resta) de las deri-
vadas de cada una de ellas.

7. Integrales inmediatas
Integrales inmediatas: una tabla de derivadas leída al revés proporciona
primitivas e integrales indefinidas.
1.- ⌡
⌠
xa
dx =
xa+1
a+1
+ C, si a ≠-1, a ∈R
2.-
⌡

⌠ 1
x
dx = ln x + C
3.- ⌡
⌠
ex
dx = ex
+ C
4.- ∫ax
= + C, si a>0, a ≠1
5.- ⌡
⌠
sen x dx = – cos x + C
6.- ⌡
⌠
cos x dx = sen x + C
7.-
8.-

8. Integrales inmediatas para funciones compuestas
•
⌡


⌠
xr
dx =
xr+1
r + 1
+ C, para cualquier constante r ≠ – 1
⌡


⌠
f '(x) [f(x)]r dx =
[f(x)]r+1
r + 1
+ C para r ≠-1
1
2 ⌡

⌠
2 cos 2x sen3 2x dx =
1
2
sen4
2x
4 =
1
8 sen4 2x + C
Tipo general
•
⌡


⌠
cos 2x sen3 2x dx =
Ejemplo:

9. Integrales inmediatas para funciones compuestas
Tipo general
Ejemplo:
∫ dx
xf
xf
)(
)('
= ln |f(x)| + C
•
⌡


⌠
tg 3x dx =
– 1
3 ⌡

⌠– 3 sen 3x
cos 3x
dx = –
1
3
ln |cos 3x | + C

10. Integrales inmediatas para funciones compuestas
Tipo general
Ejemplo:
⌡


⌠
f '(x) af(x) dx =
af(x)
ln a
+ C, para a > 0
•
⌡


⌠
x2
ex3
dx =
1
3 ⌡


⌠
3x2
ex3
dx =
1
3
ex3
+ C

11. Integrales inmediatas para funciones compuestas
Tipo general
Ejemplo:
⌡


⌠
f '(x) sen f(x) dx = – cos f(x) + C
•
⌡


⌠
e3x
sen (e3x
+ 5) dx = 1
3 ⌡


⌠
3 e3x
sen (e3x
+ 5) dx = –
1
3
cos (e3x
+ 5) + C

12. Integrales inmediatas para funciones compuestas
Tipo general
Ejemplo:
⌡


⌠
f '(x) cos f(x) dx = sen f(x) + C
•
⌡


⌠
e7x
cos (e7x
+ 5) dx =
1
7 ⌡


⌠
7 e7x
cos (e7x
+ 5) dx =
1
7
sen (e7x
+ 5) + C

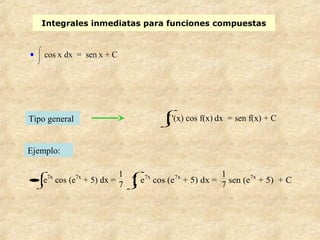
13. Integrales inmediatas para funciones compuestas
Tipo
general
Ejemplo:
⌡

⌠ g '(x)
1 - [g(x)]2 dx = arcsen g(x) + C
•
⌡

⌠ e3x
1 – e6x dx =
⌡

⌠e3x
1 – (e3x
)2 dx =
1
3 ⌡

⌠3e3x
1 – (e3x
)2 dx =
1
3
arcsen e3x
+ C

14. Integrales inmediatas para funciones compuestas
Tipo
general
•
⌡

⌠ 1
1 + 2x2 dx =
Ejemplo:
⌡

⌠ 1
1 + ( 2x)2 dx =
1
2 ⌡

⌠ 2
1 + ( 2x)2 dx =

15. Integración por partes
Es muy frecuente expresar esta fórmula con la siguiente notación abreviada que se obtiene
poniendo: u = f(x), dv = g '(x)dx, v = g(x) y du = f ' (x) dx:
⌡

⌠
u dv = uv – ⌡

⌠
v du
Consejos 1. Llamar g′ a una función de la que sea cómodo obtener g.
2. Si es cómodo obtener g sea cual fuere la elección que hagamos para
g′, llamar entonces g′ a aquella que haga que ∫ f ′g se más cómoda
que ∫ f g ′ .

16. Integración por partes: Ejemplos
= x2
ex
– 2[xex
–
⌡


⌠
ex
dx ] = ex
(x2
– 2x + 2) + C
•⌡


⌠
x2
ex
dx = x2
ex
–
⌡


⌠
ex
2x dx = x2
ex
– 2
⌡


⌠
x ex
dx =
u = x2
⇒ du = 2x dx
dv = ex
. dx ⇒ v = ex
u = x ⇒ du = dx
dv = ex
. dx ⇒ v = ex
u = sen (L x) ⇒ du = cos(L x) . (1/x) . dx
dv = dx ⇒ v = x
= x . sen(ln x) – x cos(ln x) –
⌡


⌠
sen(ln x) . dx
Despejando la integral buscada queda:
u = cos (L x) ⇒ du = – sen(L x) . (1/x) . dx
dv = dx ⇒ v = x
x . sen (ln x) –
⌡


⌠
cos (ln x) . dx =•⌡


⌠
sen(ln x) . dx =
⌡


⌠
sen(ln x) . dx =
1
2
x [sen(ln x) – cos(ln x)] + C

17. Integración por sustitución o cambio de variable
Si F es una primitiva de f, y g es derivable se tiene:
(F o g)'(x) =F(g(x))’= F '[g(x)] g'(x) = f[g(x)] g'(x)
Por lo que la integral del elemento final es:
⌡

⌠
f[g(x)]g'(x) dx = F[g(x)] + C
Si se escribe u = g(x), entonces du = g' (x) dx.
Con esta sustitución se tiene ⌡


⌠
f(u) du = F(u) + C

18. Integración por sustitución: Ejemplos I
•
⌡

⌠ 1
x ln x
dx
Cambio ln x = u ⇒ dx / x = du
= =
⌡


⌠ 1
u du = ln | u | + C
deshacer el cambio
= ln | ln x | + C
Para calcular una integral por cambio de variable:
• Buscar una transformación u = g(x) que reduzca su cálculo al de una integral
inmediata.
• Cuando se realiza el cambio debe transformarse también la diferencial
mediante.
du = g'(x) dx
• Después de calcular la integral inmediata debe deshacerse el cambio
poniendo g(x) de nuevo en lugar de u para obtener el resultado final.

19. Integración por sustitución: Ejemplos II
deshacer el cambio
•
⌡


⌠
x3
x4
+ 2 dx =
Cambio x4
+ 2 = u ⇒ 4x3
. dx = du ⇒ x3
dx = du/4
•
⌡


⌠
sen3
2x .
cos 2x dx =
1
2 ⌡


⌠
t3 .
dt =
Cambio sen 2x = t ⇒ 2 cos 2x . dx = dt ⇒ cos 2x dx =
dt/2
=
1
8
sen4
2x + C
1
2
t4
4
+ C
deshacer el cambio

20. Integración de funciones racionales
Pretendemos obtener
⌡

⌠P(x)
Q(x)
dx en donde P(x) y Q(x) son polinomios tales que
grad[P(x)] = m y grad[Q(x)] = n
Caso 1: m ≥ n. Veremos que este caso se puede convertir al Caso 2.
P(x) Q(x)
C(x)R(x)
con grad[R(x)] < grad[Q(x)]
⇔ P(x) = C(x) . Q(x) + R(x) ⇔
P(x)
Q(x)
= C(x) +
R(x)
Q(x)
Por tanto:
⌡

⌠P(x)
Q(x)
dx =
⌡


⌠
C(x) .dx +
⌡

⌠R(x)
Q(x)
dx
En donde la primera
integral es inmediata y la
segunda corresponde al
Caso 2
Caso 2: m < n. Entonces la integral se hace por descomposición en fracciones simples.
Como m ≥ n, es posible la división entera entre P(x) y Q(x)

21. Descomposición en fracciones simples I
Pretendemos obtener
⌡

⌠ P(x)
Q(x)
dx en donde P(x) y Q(x) son polinomios tales que
grad[P(x)] = m < grad[Q(x)] = n
• Supongamos que es posible factorizar el polinomio Q(x). Ello equivale a resolver la
ecuación Q(x) = 0.
• Supongamos que la ecuación Q(x) = 0 tiene:
• Soluciones reales sencillas (por ejemplo x1).
• Soluciones reales múltiples (por ejemplo x2 con orden de multiplicidad 2).
• Soluciones complejas sencillas (por ejemplo tiene dos soluciones, que
son necesariamente conjugadas).
• El caso soluciones complejas múltiples no se estudia.
Por ej. Si tiene una raíz simple una doble y dos complejas conjugadas, entonces dicho
polinomio se factoriza de la siguiente manera:
Q(x) = ao(x – x1) .
(x – x2)2 .
(x2
+ bx + c)
tal que ao es el coeficiente del término de mayor grado.
⌡

⌠P(x)
Q(x)
dx =
1
ao ⌡

⌠ P(x)
(x – x1) .
(x – x2)2 .
(x2
+ bx + c)
dx =
Paso 1. Factorización del polinomio Q(x)

22. Descomposición en fracciones simples II
Paso 2. Descomponer el integrando en fracciones simples
P(x)
(x – x1) .
(x – x2)2 .
(x2
+ bx + c)
=
A
x – x1
+
B
(x – x2)2 +
C
x – x2
+
Mx + N
x2
+ bx + c
Paso 3. Cálculo de los coeficientes indeterminados
Proceso de cálculo:
• Eliminar denominadores en la igualdad anterior, para obtener una
identidad polinómica.
• Dar valores numéricos cualesquiera, tantos como coeficientes
indeterminados (en el ejemplo 5: x1, x2 y 3 valores más).
• Resolver el sistema.

23. Descomposición en fracciones simples: ejemplo
Descomponer en fracciones simples:
x2
+ x + 1
x5
– x4
– x + 1
Paso 1. Factorización del polinomio denominador
Por Ruffini obtenemos: x5
– x4
– x + 1 = (x + 1) .
(x – 1)2 .
(x2
+ 1)
Paso 2. Descomponer en fracciones simples
x2
+ x + 1
x5
– x4
– x + 1
=
A
x + 1
+
B
(x – 1)2 +
C
x – 1
+
Mx + N
x2
+ 1
Paso 3. Cálculo de los coeficientes indeterminados
x2
+ x + 1= A(x–1)2
(x2
+1) + B(x+1)(x2
+1) + C(x–1)(x+1)(x2
+1) + (Mx+N) (x+1)(x–1)2




x=1 →B=3/4
x=–1 →A=1/8
x=0 →– C + N = 1/8
x=2 →5C+2M+N = –13/8
x=–2 →5C+6M–3N = 3/8
Y de aquí: A = 1/8; B = 3/4; N = –1/4; C = –3/8; M = 1/4

24. Integrales racionales con denominador de grado 2
Estudio de la integral
⌡

⌠Mx + N
ax2
+ bx + c
dx
Sea D el discriminante del
denominador: D = b2
– 4ac
Si la derivada del denominador es el numerador salvo una constante, la integral podrá ser
resuelta como inmediata tipo neperiano.
En caso contrario:
• Si D ≥ 0 ⇒ la integral se obtiene por descomposición en fracciones simples.
• Si D < 0 ⇒ la integral es tipo neperiano + arco tangente.
Pasos para su obtención:
M ≠ 0
Paso 1: se busca la derivada del denominador en el numerador.
Paso 2: como consecuencia se puede descomponer la integral en suma de otras
dos: la primera es inmediata (neperiano) y la segunda es tipo arco tangente.
M = 0 (Cálculo de la integral tipo arco tangente).
Paso3: se convierte el denominador en un número (k) más un binomio al cuadrado
(cosa que es posible por ser D < 0). Si previamente se multiplica por 4a se evitan
los números fraccionarios.
Paso 4: se convierte el denominador en la unidad más una función al cuadrado
(sacando factor común k en el denominador), ajustamos con constantes, e
integramos como inmediata tipo arco tangente

25. Integración de funciones trigonométricas:
fórmulas
Fórmulas trigonométricas fundamentales
sen2
px + cos2
px = 1
Fórmula fundamental de la
trigonometría.
sen 2px = 2 sen px . cos px
cos 2px = cos2
px – sen2
px
Seno y coseno del ángulo
doble.
cos2
px =
1 + cos 2px
2
sen2
px =
1 – cos 2px
2
Fórmulas de reducción de
grado.
sen a . cos b =
1
2 sen (a + b) +
1
2 sen (a – b)
cos a . cos b =
1
2 cos (a + b) +
1
2 cos (a – b)
sen a . sen b = –
1
2
cos (a + b) +
1
2
cos (a – b)
Fórmulas de conversión de
productos de senos y
cosenos en suma.
sen (– px) = – sen px
cos (– px) = cos px
Seno y coseno del ángulo
opuesto.
1 + tg2
px = sec2
px;
1 + ctg2
px = csc2
px

26. Integración de funciones trigonométricas: métodos
Forma Condiciones Método
n par
Reducir el grado del integrando por medio de
las fórmulas de reducción de grado (3), según
convenga.(I) ⌡

⌠
senn
px dx
⌡

⌠
cosn
px dx
n impar
Sacar un factor (seno o coseno) de la potencia
sustituyendo en el resto de la potencia la rela-
ción 1. Al desarrollar la potencia se obtienen
integrales inmediatas tipo potencial.
m y n pares Reducir el grado del integrando aplicando las
fórmulas 3.
(II)⌡

⌠
senn
px . cosn
px dx
m ó n impares
De la potencia de exponente impar se saca un
factor, sustituyendo en el resto de la potencia la
relación 1. Al desarrollar la potencia se obtie-
nen integrales inmediatas tipo potencial.
Caso particular  Si m = n Aplicar la relación (2a) para obtener:
⌡

⌠
senn
px . cosn
px dx =
1
2n
⌡

⌠
senn
2px dx
que es del tipo (I).

27. Forma Condiciones Método
(III)
⌡

⌠
sen px.cos qx.dx
⌡

⌠
sen px.sen qx.dx
⌡

⌠
cos px.cos qx..dx
p y q números
reales cuales-
quiera
Convertir los productos en sumas mediante la
relaciones 4 según convenga.
Integración de funciones trigonométricas: métodos II

28. Integración de funciones trigonométricas: ejemplos I
= ⌡

⌠
sen3x.dx +⌡

⌠
cos4
3x sen 3x.dx –2⌡

⌠
cos2
3x sen 3x.dx =
= –
1
3
cos 3x -
2
9
cos3
3x +
1
15
cos5
3x+C
Tipo I. Exponente impar
=
1
4
x +
1
4 ⌡

⌠1 + cos
4x
3
2
dx –
3
4
sen
2x
3
=
3x
8
–
3
4
sen
2x
3
+
3
32
sen
4x
3
+ C
Tipo I. Exponente par
•⌡

⌠
sen5
3x.dx = ⌡

⌠
(sen2
3x)2
sen 3x.dx = ⌡

⌠
(1–cos2
3x)2
sen 3x.dx =
•
⌡


⌠
sen4 x
3 dx = 1
4 ⌡

⌠






1 + cos2 2x
3
– 2 cos
2x
3
dx =⌡

⌠








sen2 x
3
2
dx =
⌡

⌠





1 – cos
2x
3
2
2
dx =
=
1
4 ⌡

⌠
1.dx +
1
4 ⌡


⌠
cos2 2x
3 dx – 2
1
4 ⌡


⌠
cos
2x
3 dx =

29. Integración de funciones trigonométricas: ejemplos
II
Tipo II. Al menos un exponente impar
•⌡


⌠
cos4
5x.sen3
5xdx =
⌡


⌠
cos4
5x . sen2
5x .sen 5x . dx =
⌡


⌠
cos4
5x . (1 – cos2
5x).sen 5x.dx =
=
⌡


⌠
cos4
5x.sen 5x.dx –
⌡


⌠
cos6
5x.sen 5x.dx =
=
– 1
25
cos5
5x +
1
35
cos7
5x + C
=
1
8 ⌡

⌠1 – cos 12x
2
dx –
1
48
sen3
6x
3
=
=
1
8 ⌡


⌠
sen2
6x dx –
1
8 ⌡


⌠
sen2
6x .cos 6x.dx =
=
x
16
–
1
144
sen3
6x –
1
192
sen 12x + C
Tipo II. Todos los exponentes pares
•⌡


⌠
sen4
3x .cos2
3x.dx =
⌡


⌠
(sen2
3x)2
.cos2
3x.dx =
⌡

⌠





1 – cos 6x
2
2 1 + cos 6x
2
dx =
=
1
8 ⌡


⌠
(1 – cos 6x)(1 – cos2
6x) dx =
( 1 – cos 6x) ( 1 – cos 6x) ( 1 + cos 6x)
( 1 – cos 6x) ( 1 – cos2
6x)
sen2
6x

30. Integración de funciones trigonométricas: ejemplos III
Tipo III: Producto de funciones con distinto argumento
•⌡


⌠
sen 3x.cos 5x.dx = 1
2 ⌡


⌠
sen 8x .dx +
1
2 ⌡


⌠
sen( – 2x) .dx =
= –
1
16
cos 8x +
1
4
cos( – 2x) + C == –
1
16
cos 8x +
1
4
cos 2x + C
Para resolverlas hay que utilizar las fórmulas de trasformación de sumas
en productos

31. Cálculo de áreas
• En multitud de problemas que se presentan en Ciencia y Tecnología es preciso
calcular el área encerrada por varias curvas.
• Este problema pasa por encontrar el área limitada por una curva y = f(x), el eje OX y
las abcisas x = a, x = b.
Área (Trapecio rectilíneo) =
=
f(a) + f(b)
2
.
(b – a)
Área (Trapecio curvilíneo) ≈
≈
f(a) + f(b)
2
.
(b – a)
Error