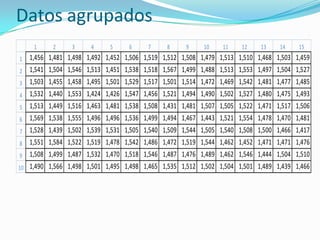
Este documento explica paso a paso cómo convertir datos agrupados en intervalos aparentes. Primero se encuentran el valor máximo y mínimo para calcular el rango de los datos. Luego se determina el número y tamaño de los intervalos, y se construyen las tablas de límites inferiores y superiores sumando progresivamente el tamaño de intervalo. El objetivo es que los límites cumplan con las reglas de ser mayores o iguales a los valores mínimo y máximo.

1. Estadística
Datos agrupados
Intervalos aparentes.

2. INTRODUCCIÓN
 En esta presentación explicare una tabla de datos
agrupados paso por paso.
 El objetivo es mostrar detalladamente las operaciones
necesarias para convertir datos agrupados en
intervalos aparentes.
 En esta ocasión explicare con números decimales.

3. Datos agrupados
 Procedimiento:
 Realizar la tabla estadística para los siguientes datos
agrupados en 9 intervalos.

4. Datos agrupados
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 1,456 1,481 1,498 1,492 1,452 1,506 1,519 1,512 1,508 1,479 1,513 1,510 1,468 1,503 1,459
2 1,541 1,504 1,546 1,513 1,451 1,538 1,518 1,567 1,499 1,488 1,513 1,553 1,497 1,504 1,527
3 1,503 1,455 1,458 1,495 1,501 1,529 1,517 1,501 1,514 1,472 1,469 1,542 1,481 1,477 1,485
4 1,532 1,440 1,553 1,424 1,426 1,547 1,456 1,521 1,494 1,490 1,502 1,527 1,480 1,475 1,493
5 1,513 1,449 1,516 1,463 1,481 1,538 1,508 1,431 1,481 1,507 1,505 1,522 1,471 1,517 1,506
6 1,569 1,538 1,555 1,496 1,496 1,536 1,499 1,494 1,467 1,443 1,521 1,554 1,478 1,470 1,481
7 1,528 1,439 1,502 1,539 1,531 1,505 1,540 1,509 1,544 1,505 1,540 1,508 1,500 1,466 1,417
8 1,551 1,584 1,522 1,519 1,478 1,542 1,486 1,472 1,519 1,544 1,462 1,452 1,471 1,471 1,476
9 1,508 1,499 1,487 1,532 1,470 1,518 1,546 1,487 1,476 1,489 1,462 1,546 1,444 1,504 1,510
10 1,490 1,566 1,498 1,501 1,495 1,498 1,465 1,535 1,512 1,502 1,504 1,501 1,489 1,439 1,466

5. Datos agrupados
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
1,525 1,472 1,476 1,536 1,500 1,477 1,550 1,531 1,516 1,504 1,447 1,492 1,513 1,495 1,513
1,506 1,563 1,453 1,488 1,472 1,507 1,542 1,477 1,499 1,551 1,507 1,453 1,507 1,492 1,486
1,508 1,472 1,525 1,436 1,502 1,468 1,495 1,499 1,512 1,536 1,489 1,514 1,588 1,475 1,510
1,530 1,560 1,487 1,469 1,466 1,478 1,482 1,508 1,515 1,493 1,558 1,480 1,489 1,467 1,530
1,477 1,581 1,515 1,458 1,498 1,521 1,534 1,469 1,514 1,499 1,463 1,512 1,493 1,513 1,533
1,488 1,454 1,430 1,530 1,550 1,472 1,499 1,501 1,502 1,501 1,447 1,518 1,501 1,529 1,534
1,504 1,441 1,470 1,498 1,497 1,525 1,520 1,526 1,486 1,473 1,511 1,466 1,503 1,412 1,502
1,503 1,485 1,476 1,528 1,517 1,485 1,463 1,559 1,517 1,553 1,465 1,526 1,475 1,511 1,516
1,504 1,553 1,449 1,507 1,469 1,455 1,490 1,475 1,528 1,482 1,492 1,527 1,489 1,487 1,482
1,553 1,549 1,488 1,474 1,571 1,451 1,462 1,454 1,440 1,477 1,516 1,532 1,541 1,489 1,548

6. Datos agrupados
 Primer paso:
 Encontrar en los datos el valor máximo y el mínimo
para calcular el rango.
 Valor máximo = 1,588
 Valor mínimo= 1,412
 Rango= 1,588 - 1,412
 Rango= 0,176

7. Datos agrupados
 Segundo paso:
 Determinar el número de intervalos en que se van a
agrupar los datos. El número de intervalos se puede
calcular obteniendo la raíz cuadrada del número de
datos: = 20
 Se tomarían 20 intervalos.
 Pero tu puedes establecer el número de intervalos.
Vamos afijarlo en 9

8. Datos agrupados
 Tercer paso:
 Determinar el tamaño del intervalo
 Se divide el rango entre el número de intervalos: 0,176
÷ 9 = 0,0195
 Como los datos son con 3 decimales, se toma un
tamaño de intervalo redondeado , podría ser 0,019 ó
0,020. Vamos a tomar el 0,019 y veamos cómo quedan
los intervalos.

9. Datos agrupados
 Cuarto paso:
 Construir los 9 intervalos aparentes . Para realizar este
paso se pueden hacer puchas cosas pero les voy a
enseñar una muy sencilla. Se elige un valor inicial para
que sea el primer límite inferior. Debe ser menor o
igual al valor mínimo. Vamos a elegir el 1,412 .

10. Datos agrupados
# de intervalo Limite Inferior Limite Superior
1 1,412
2 Este valor inicial
3 debe ser menor o
igual al mínimo, se
4
puede elegir otro
5
numero menor. se
6 puede cambiar
7 encaso necesario.
8
9

11. Datos agrupados
 Cuarto paso:
 A partir de este valor inicial se calculan los 9 límites
inferiores. Se suma a cada límite el tamaño del
intervalo.

12. Datos agrupados
# de intervalo Limite Inferior Limite Superior
1 1,412 Se sumara el tamaño
2 1,431 del intervalo.
3 1,450 1,412 + 0,019 = 1,431
4 1,469 1,431 + 0,019 = 1,450
5 1,488
6 1,507
7 1,526
8 1,545
9 1,564

13. Datos agrupados
 Debemos revisar que el último límite inferior sea menor o
igual al valor máximo.
En este caso sí se cumple: 1,564 ≤ 1,588
Ahora vamos a obtener el primer límite superior.
Como los datos son con 3 decimales se le resta 0,001. en
caso que sea entero se le resta un entero y esto seria al
segundo límite inferior:
Segundo límite inferior = 1,431
Menos un decimal = 1,430
El primer límite superior será: 1,430

14. Datos agrupados
# de intervalo Limite Inferior Limite Superior
Aquí ya se le
1 1,412 1,430
2 1,431
resto un decimal
3 1,450 como esta
4 1,469 explicado en la
5 1,488 diapositiva
6 1,507 anterior
7 1,526
8 1,545
9 1,564

15. Datos agrupados
 Cuarto paso: finalmente se le suma el tamaño del
intervalo como se le sumo a limite inferior:
1,430 + 0,019 = 1,449
1,449 + 0,019 = 1,468
otra forma seria cruzar el valor, el tercer valor del
limite inferior pasaría hacer el segundo valor del limite
superior menos 0,001 como lo siguiente:

16. Datos agrupados
# de intervalo Limite Inferior Limite Superior
1 1,412 1,430 Notaran que
2 1,431 1,449
el resultado
es el mismo
3 1,450 1,468
sumándole o
4 1,469 1,487
cruzándolo.
5 1,488 1,506
6 1,507 1,525
7 1,526 1,544
8 1,545 1,563
9 1,564 1,582

17. Datos agrupados
 Cuarto paso
 Ya esta listo solo falta revisar si todo cumple con las
reglas:
 El primer límite superior debe ser mayor o igual al
valor mínimo.
 El último límite superior debe ser mayor o igual al
valor máximo

18. Datos agrupados
# de intervalo Limite Inferior Limite Superior
1 1,412 1,430 El ultimo valor
2 1,431 1,449 del limite
3 1,450 1,468 superior no
cumple con la
4 1,469 1,487
regla de que debe
5 1,488 1,506 ser mayor o igual
6 1,507 1,525 que el máximo.
7 1,526 1,544 Entonces queda
8 1,545 1,563 cambiar el
tamaño del
9 1,564 1,582 intervalo a 0,020
veamos como
queda.

19. Datos agrupados
 Repitamos el mismo procedimiento.
 Sumarle el tamaño del intervalo que aora será 0,020 al
limite inferior y posteriormente al limite superior, y la
tabla quedara asi:

20. Datos agrupados
Notaran que las
# de intervalo Limite Inferior Limite Superior cuatro esquinas
1 1,412 1,431 están en rojo, esto
es por que si se
2 1,432 1,451
cumplieron las
3 1,452 1,471 siguientes reglas:
4 1,472 1,491
El primer límite
5 1,492 1,511 superior debe ser
6 1,512 1,531 mayor o igual al
7 1,532 1,551 valor mínimo.
8 1,552 1,571 El último límite
9 1,572 1,591 superior debe ser
mayor o igual al
valor máximo

21. Datos agrupados
 Cuarto paso:
 Finalmente hemos obtenido los intervalos aparentes.
Estos intervalos son útiles para contar los datos cuando
hay que hacerlo manualmente, pero en la tabla deben
anotarse los intervalos reales. Después les explicare
como sacar los intervalos reales.

22.  Soel_leos@hotmail.es
 http://leyna-estadistica.bligoo.com.mx/
 Gracias por su atención