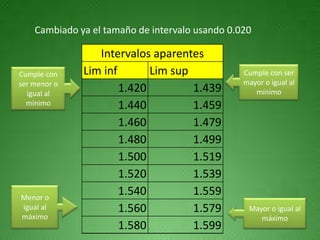
Este documento presenta los pasos para construir una tabla de intervalos aparentes a partir de un conjunto de datos numéricos. Primero se determinan el valor máximo y mínimo para calcular el rango e intervalos. Luego se construye la tabla siguiendo cuatro normas: que el límite inferior inicial sea menor o igual al mínimo, que los límites superiores sean mayores o iguales al mínimo, que los límites inferiores subsiguientes se obtengan sumando el tamaño de intervalo, y que el límite superior final sea mayor o igual al máximo.

2. Introducción
En esta presentación se construye una
tabla donde se muestra el procedimiento
Para formar los intervalos aparentes
El objetivo es mostrar las operaciones
aritméticas necesarias para llevar
acabo lo mencionado anteriormente.

3. Datos Agrupados
1.525 1.487 1.513 1.543 1.555 1.490 1.471 1.533 1.484 1.524 1.504
1.501 1.517 1.532 1.545 1.506 1.504 1.464 1.422 1.575 1.529 1.490
1.518 1.545 1.593 1.500 1.506 1.545 1.541 1.476 1.530 1.463 1.489
1.512 1.505 1.490 1.481 1.508 1.511 1.523 1.526 1.489 1.527 1.508
1.473 1.480 1.521 1.466 1.462 1.484 1.488 1.469 1.514 1.519 1.504
1.555 1.478 1.544 1.493 1.513 1.461 1.542 1.508 1.496 1.450 1.487
1.516 1.532 1.448 1.503 1.504 1.547 1.508 1.475 1.471 1.511 1.493
1.492 1.464 1.535 1.494 1.523 1.497 1.518 1.502 1.513 1.532 1.505

4. Datos Agrupados
1.502 1.507 1.484 1.507 1.495 1.533 1.478 1.515 1.490 1.483 1.524
1.444 1.470 1.509 1.514 1.538 1.458 1.455 1.511 1.456 1.461 1.507
1.469 1.468 1.526 1.487 1.468 1.467 1.474 1.482 1.556 1.510 1.489
1.537 1.457 1.517 1.485 1.513 1.544 1.493 1.450 1.463 1.532 1.468
1.538 1.539 1.502 1.477 1.462 1.450 1.533 1.586 1.568 1.433 1.551
1.511 1.434 1.424 1.532 1.534 1.545 1.472 1.454 1.525 1.511 1.501
1.461 1.475 1.474 1.505 1.504 1.502 1.559 1.474 1.527 1.454 1.475

5. Datos Agrupados
1.485 1.506 1.479 1.463 1.538 1.461 1.420 1.492 1.425
1.477 1.511 1.548 1.522 1.477 1.486 1.477 1.451 1.456
1.487 1.507 1.458 1.495 1.486 1.481 1.553 1.513 1.506
1.452 1.544 1.460 1.522 1.513 1.501 1.461 1.521 1.509
1.485 1.531 1.516 1.497 1.505 1.521 1.528 1.519 1.491
1.502 1.535 1.508 1.503 1.506 1.487 1.586 1.481 1.545
1.486 1.544 1.454 1.526 1.498 1.446 1.511 1.515 1.458
1.500 1.511 1.506 1.506 1.506 1.496 1.544 1.494 1.550
1.515 1.462 1.541 1.546 1.566 1.519 1.502 1.493 1.494
1.426 1.471 1.475 1.537 1.572 1.487 1.533 1.542 1.472
1.480 1.484 1.434 1.564 1.506 1.496 1.489 1.499 1.518
1.514 1.487 1.557 1.527 1.445 1.496 1.466 1.509 1.494
1.556 1.534 1.515 1.518 1.449 1.472 1.473 1.478 1.504
1.479 1.479 1.478 1.508 1.478 1.506 1.540 1.474 1.505
1.498 1.508 1.524 1.519 1.528 1.478 1.504 1.486 1.46
7

6. Datos Agrupados
El primer paso es encontrar el máximo y el mínimo del
conjunto de datos para asi poder
Calculas el rango
En este ejemplo los valores son:
Maximo:1.593
Minimo:1.420
Rango:1.593-1.420=0.173
El segundo paso es determinar el numero
de intervalos para asi poder obtener
El tamaño del intervalo en este caso
No de intervalos =9 tamaño de intervalo=rango/9
Tamaño del intervalo = 0.019

7. Datos Agrupados
El tercer paso es construir la tabla de los intervalos aparentes
existen 4 normas que se
Tiene que cumplir en la realización de esta tabla
Primera norma: primer limite inferior debe ser menor o igual al
mínimo.
Intervalos Aparentes
Limite Límite
Menor o inferior superior
Igual al 1.420
Mínimo

8. Para seguir con la construcción de la tabla ya teniendo establecido
el primer limite inferior a este se va sumando el tamaño del
intervalo para asi obtener el resto de los limites inferiores.
Intervalos aparentes
1.420+0.019=
Lim. Inf. Lim. Sup.
Suma del 1.420
intervalo 1.439
anterior mas
el Tamaño 1.458
de intervalo 1.477
1.496
1.515
1.534
Hasta obtener
los intervalos 1.553
establecidos 1.572

9. La segunda norma que se tiene que
cumplir es que el ultimo limite inferior sea menor
o igual al máximo. Intervalos aparentes
Lim. Inf. Lim. Sup.
1.420
1.439
1.458
1.477
1.496
1.515
1.534
Igual o menor al
máximo en este caso si
1.553
se cumple por que es 1.572
menor que 1.593

10. Para seguir construyendo la tabla el primer limite superior se obtiene
restándole al segundo limite inferior 0.001 ya que se tiene 3 decimales
si fuera 2 se restari0.002 ,si fuera entero se le restaría 1 .
Este limite debe cumplir con la tercera norma ser Mayor o igual al
mínimo
Intervalos aparentes
Lim inf Lim sup A 1.439-0.001=1.438
Mayor o igual al mínimo
1.420 1.438 En este caso si se cumple por
1.439 que si es mayor que el mínimo
1.458
1.477
1.496
1.515
1.534
1.553
1.572

11. Los siguientes limites superiores se determinan de la siguiente manera
Al primer limite superior se le va sumando
El tamaño del intervalo hasta tener los intervalos establecidos.
Intervalos aparentes
Lim inf. Lim sup.
Se suma el tamaño
1.420 1.438
del intervalo al
1.439 1.457 limite anterior
1.458 1.476 1.438+0.001=1.457
1.477 1.495
1.496 1.514
1.515 1.533
1.534 1.552
1.553 1.571
1.572 1.590

12. La cuarta y ultima norma es que el ultimo limite superior
debe ser Mayor o igual al máximo.
Intervalos aparentes
Lim inf Lim sup
1.420 1.438
1.439 1.457
1.458 1.476
1.477 1.495
1.496 1.514
1.515 1.533
1.534 1.552
Mayor o igual al máximo en este
1.553 1.571 caso no se cumple por que
1.572 1.590 1.590 no es mayor o igual al
máximo

13. Cuarto paso si las cuatro normas no se cumplen se
puede cambiar el tamaño
de intervalo es decir ya que usábamos 0.019 a
hora usaremos 0.020 ya que se aplica
un redondeo, se aplica en mismo procedimiento
pero ahora utilizando el tamaño de intervalo
nuevo (0.020) existen casos donde tampoco se
cumplirán las cuatro normas aun cambiando el
tamaño de intervalo y en ese caso se recomienda
cambiar d numero de intervalos usando 10 o 8
etc.

14. Cambiado ya el tamaño de intervalo usando 0.020
Intervalos aparentes
Cumple con Lim inf Lim sup Cumple con ser
ser menor o mayor o igual al
igual al
1.420 1.439 mínimo
mínimo 1.440 1.459
1.460 1.479
1.480 1.499
1.500 1.519
1.520 1.539
Menor o
1.540 1.559
igual al 1.560 1.579 Mayor o igual al
máximo máximo
1.580 1.599

15. Finalmente se obtuvieron ya las
intervalos aparentes los cuales son
útiles para obtener los intervalos
reales en próximas presentaciones
se mostrara en procedimiento
para obtenerlos .

16. http://www.deacosta.bligoo.com.mx/
Loki_adri15@hotmail.com