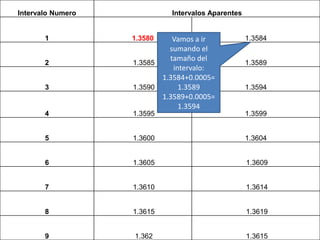
Este documento describe los pasos para agrupar un conjunto de datos en intervalos. Explica cómo calcular el rango de los datos, determinar el número de intervalos, el tamaño de cada intervalo y establecer los límites inferiores y superiores de los intervalos. A través de un ejemplo, muestra cómo aplicar estos pasos para obtener una tabla de intervalos aparentes que resuma los datos de manera agrupada.

1. Introducción
En esta presentación se construye una tabla de
datos agrupados paso por paso. El objetivo es
mostrar detalladamente las operaciones
aritméticas necesarias para resumir un conjunto
de datos agrupándolos en intervalos.
Se incluye el calculo de intervalos aparentes.

2. Datos Agrupados
Procedimiento para datos agrupados.
Ejemplo:
Completa la tabla estadística para los siguientes
datos agrupándolos en 9 intervalos.

3. Datos Agrupados
• 1 1.476 1.457 1.534 1.498 1.497 1.407 1.465 1.505 1.496
1.520 1.599 1.484 1.494 1.577 1.557 1.495 1.589 1.571
1.520 1.536
• 2 1.543 1.551 1.526 1.510 1.469 1.524 1.470 1.459 1.510
1.516 1.464 1.508 1.505 1.497 1.454 1.527 1.465 1.447
1.550 1.449
• 3 1.452 1.505 1.516 1.477 1.456 1.597 1.522 1.499 1.473
1.507 1.561 1.464 1.460 1.469 1.566 1.453 1.441 1.444
1.497 1.433
• 4 1.457 1.540 1.494 1.541 1.490 1.539 1.448 1.459 1.493
1.500 1.444 1.544 1.500 1.486 1.503 1.480 1.554 1.492
1.523 1.498
• 5 1.525 1.463 1.402 1.533 1.514 1.522 1.536 1.537 1.470
1.489 1.470 1.548 1.504 1.489 1.467 1.548 1.504 1.535
1.506 1.507
• 6 1.471 1.512 1.456 1.514 1.412 1.568 1.564 1.449 1.447
1.530 1.470 1.484 1.467 1.397 1.582 1.477 1.533 1.480
1.553 1.486
• 7 1.556 1.422 1.552 1.498 1.533 1.542 1.516 1.448 1.481
1.516 1.479 1.441 1.519 1.496 1.576 1.496 1.475 1.459
1.462 1.500
• 8 1.473 1.530 1.523 1.464 1.520 1.527 1.501 1.483 1.437
1.529 1.527 1.364 1.556 1.513 1.480 1.446 1.474 1.480
1.504 1.492
• 9 1.469 1.495 1.524 1.455 1.488 1.517 1.502 1.436 1.572
1.516 1.541 1.537 1.506 1.479 1.441 1.490 1.567 1.517
1.468 1.501
• 10 1.585 1.537 1.444 1.562 1.540 1.495 1.456 1.536 1.541
1.487 1.489 1.463 1.526 1.555 1.483 1.528 1.512 1.452
1.435 1.430
• 11 1.508 1.449 1.443 1.593 1.485 1.421 1.610 1.445 1.540
1.474 1.507 1.449 1.519 1.549 1.444 1.533 1.517 1.509
1.492 1.491
• 12 1.448 1.564 1.395 1.511 1.529 1.430 1.564 1.429 1.523
1.455 1.465 1.487 1.519 1.470 1.492 1.539 1.477 1.526
1.454 1.468
• 13 1.515 1.472 1.493 1.486 1.541 1.492 1.476 1.468 1.456
1.468 1.490 1.563 1.495 1.543 1.483 1.515 1.560 1.563
1.609 1.472
• 14 1.525 1.523 1.535 1.497 1.510 1.543 1.442 1.531 1.529
1.527 1.509 1.401 1.530 1.537 1.430 1.474 1.527 1.531
1.451 1.524
• 15 1.466 1.528 1.509 1.496 1.458 1.559 1.522 1.484 1.428
1.596 1.484 1.519 1.530 1.431 1.512 1.507 1.513 1.536
1.527 1.467

4. Datos Agrupados
En las tres presentaciones anteriores “Datos
Agrupados 01,02 y 03” se llevaron a cabo los
primeros 10 pasos obteniendo los intervalos
aparentes.
El resultado de este proceso fue la siguiente
tabla:

5. Datos Agrupados
Intervalos Aparentes
Limite Inferior Limite Superior
1.358 1.375
1.376 1.393
1.394 1.411
1.412 1.429
1.430 1.447
1.448 1.465
1.466 1.483
1.484 1.501
1.502 1.519

6. Datos Agrupados
Primer Paso:
Encontrar en los datos el valor máximo y el
mínimo para calcular el rango.
Valor Máximo: 1.610
Valor Mínimo: 1.364
Rango: 1.610-1.364
Rango: 0.246

7. Datos Agrupados
Segundo Paso:
Determinar el numero de intervalos en que
se van a agrupar los datos. Existen varias
formas:
El numero de intervalos se puede calcular
obteniendo la raíz cuadrada del numero de datos:
La raíz de 300= 17.3205
Se tomarían 9 intervalos.
Otra forma consiste en establecer arbitrariamente
el numero de intervalos.

8. Datos Agrupados
Tercer Paso:
Determinar el tamaño del intervalo.
Se divide el rango entre el numero de
Intervalos: 0.246/9= 0.027
Como los datos son enteros, se toma un
tamaño del intervalo también entero, va ser
ser 0.027. Vamos a tomar el 0.027 y
veamos cómo quedan los intervalos.

9. Datos Agrupados
Cuarto Paso:
Construir los 9 intervalos aparentes.
Existen muchas formas de llevar a cabo este
paso debido a que son solo operaciones
aritméticas.
Se elige un valor inicial para que sea el primer
límite inferior. Debe ser menor o igual al valor
máximo. Vamos a elegir el 1.358.

10. Datos Agrupados
Intervalo Numero Intervalos Aparentes
1 1.3580
2
3 Este valor inicial
debe ser menor o
4 igual al mínimo
5
6
7
8
9

11. Datos Agrupados
Cuarto Paso:
A partir de este valor inicial se calculan los 9
limites inferiores.
Se va sumando a cada límite el tamaño del
intervalo como se muestra en la siguiente
diapositiva.

12. Intervalo Numero Intervalos Aparentes
1 1.3580
2 1.3585
Vamos ir sumando el
tamaño del intervalo:
3 1.3590 1.358+0.0005=1.3585
4 1.3595
5 1.3600
6 1.3605
7 1.3610
8 1.3615
9 1.3620

13. Datos Agrupados
Cuarto Paso:
Antes de continuar debemos revisar que el
ultimo límite inferior sea menor o igual al valor
máximo.
En este caso si se cumple: 1.574 menor o igual
1.610.

14. Intervalo Numero Intervalos Aparentes
1 1.3580
2 1.3585
3 1.3590
4 1.3595
5 1.3600
6 1.3605 Este límite debe ser:
Menor o Igual al valor máximo
1.574 menor o igual al máximo
7 1.3610
1.610
8 1.3615
9 1.3620

15. Datos Agrupados
Cuarto Paso:
Ahora vamos a obtener el primer límite
superior.
Como los datos son enteros se le resta un
entero al segundo límite inferior.
Segundo Límite Inferior:1.385
Menos un entero:1.384
El primer limite superior será 1.384

16. Intervalo Numero Intervalos Aparentes
1 1.3580
1.385-0.001= 1.384
2 1.3585
3 1.3590 Se resta un
entero porque los
datos son
4 1.3595 enteros; si tienen
un decimal se
resta 0.1 y si
5 1.3600
tiene dos, se
resta 0.01
6 1.3605
7 1.3610
8 1.3615
9 1.3620

17. Datos Agrupados
Cuarto Paso:
Finalmente, vamos a sumar el tamaño del
intervalo a cada límite superior en forma similar a
lo que se llevó a cabo con los límites inferiores.
1.384+0.0005= 1.3845
1.3845+0.0005= 1.3850

18. Intervalo Numero Intervalos Aparentes
1 1.3580 Vamos a ir 1.3584
sumando el
tamaño del
2 1.3585 1.3589
intervalo:
1.3584+0.0005=
3 1.3590 1.3589 1.3594
1.3589+0.0005=
1.3594
4 1.3595 1.3599
5 1.3600 1.3604
6 1.3605 1.3609
7 1.3610 1.3614
8 1.3615 1.3619
9 1.362 1.3615

19. Datos Agrupados
Cuarto Paso:
Ya están calculados los intervalos, sin embargo,
debemos revisar que se cumplan otras dos
condiciones:
El primer límite superior debe ser mayor o igual al
valor mínimo.
El ultimo límite superior debe ser mayor o igual al
valor máximo.

20. Intervalo Numero 1.3580 Intervalos Aparentes 1.3684
menor o mayor o
igual que igual que
1 1.3580 1.3684
1.364 1.364
2 1.3585 1.3589
3 1.3590 1.3594
4 1.3595 Cuatro valores 1.3599
cumplen con las
condiciones
5 1.3600 1.3604
necesarias.
6 1.3605 1.3609
7 1.3610 1.3614
1.3620 1.6155
8 1.3615 1.3619
menor o mayor o
igual que igual que
9 1.610 1.3620 1.3615 1.610

21. Datos Agrupados
Cuarto Paso:
Finalmente hemos obtenido los intervalos
aparentes.
Estos intervalos son útiles para contar los datos
cuando hay que hacerlo manualmente, pero en la
tabla deben anotarse los intervalos reales.
En la siguiente presentación continuaremos con
el paso 5. Obtener intervalos reales.

22. Gracias por su atención
Windo_cesarin@live.com.mx
http://estrada.bligoo.com.mx/