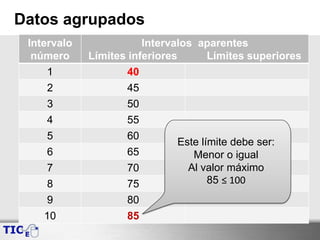
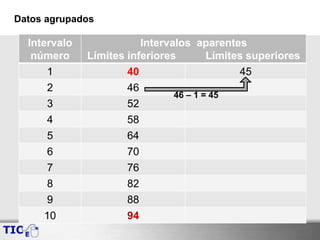
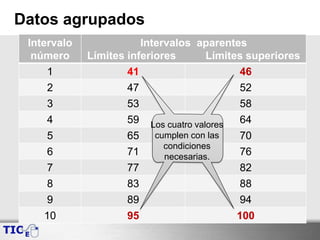
Este documento presenta los pasos para agrupar un conjunto de datos en intervalos para facilitar su análisis. Inicialmente se calculan el valor máximo, mínimo y rango de los datos. Luego se determina el número de intervalos y su tamaño. Con esta información se construyen los límites inferiores y superiores de cada intervalo, revisando que cumplan ciertas condiciones. Finalmente, se ajustan algunos valores como el número de intervalos o tamaño para que todos los límites cumplan con las condiciones requeridas.

1. Datos Agrupados
G. Edgar Mata Ortiz

2. Introducción
Cuando el número de categorías es
demasiado grande, por ejemplo mayor a
25, la tabla de distribución de frecuencias
quedaría muy grande
Al ser tan grande esta tabla de distribución
de frecuencias, no resulta útil como
herramienta para organizar y presentar la
información.
En este caso se recurre a la agrupación de
datos

3. Introducción
En estas presentaciones se construye una tabla
de datos agrupados, paso por paso.
El objetivo es mostrar detalladamente las
operaciones aritméticas necesarias para resumir
un conjunto de datos agrupándolos en
intervalos.
Se incluye el cálculo de intervalos aparentes y
reales además de las medidas de tendencia
central y dispersión más usuales.

4. Introducción
Lím. Inferior Lím. Superior
1.4125 1.4285 1.4205 3 3 0.010000 0.010000 4.26 0.25184 0.02114
1.4285 1.4445 1.4365 7 10 0.023333 0.033333 10.06 0.47563 0.03232
1.4445 1.4605 1.4525 19 29 0.063333 0.096667 27.60 0.98699 0.05127
1.4605 1.4765 1.4685 33 62 0.110000 0.206667 48.46 1.18624 0.04264
1.4765 1.4925 1.4845 46 108 0.153333 0.360000 68.29 0.91755 0.01830
1.4925 1.5085 1.5005 62 170 0.206667 0.566667 93.03 0.24469 0.00097
1.5085 1.5245 1.5165 55 225 0.183333 0.750000 83.41 0.66293 0.00799
1.5245 1.5405 1.5325 28 253 0.093333 0.843333 42.91 0.78549 0.02204
1.5405 1.5565 1.5485 26 279 0.086667 0.930000 40.26 1.14539 0.05046
1.5565 1.5725 1.5645 11 290 0.036667 0.966667 17.21 0.66059 0.03967
1.5725 1.5885 1.5805 9 299 0.030000 0.996667 14.22 0.68448 0.05206
1.5885 1.6045 1.5965 0 299 0.000000 0.996667 0.00 0.00000 0.00000
1.6045 1.6205 1.6125 0 299 0.000000 0.996667 0.00 0.00000 0.00000
1.6205 1.6365 1.6285 1 300 0.003333 1.000000 1.63 0.12405 0.01539
0 0.00% 100.00%
#N/A #N/A #N/A #N/A
Totales 451.33 8.13 0.35
Media a = 1.50445
0.02709
0.0011808
0.0343627
Desviación media =
Clases o categorías Marcas de
clase
Medidas de tendencia central y
dispersiónIntervalos
Frecuencias
Varianza =
Desviación estándar=

5. Datos agrupados
Procedimiento para datos agrupados
Ejemplo: Completa la tabla estadística para los
siguientes datos, agrupándolos en 10 intervalos.
Posteriormente trazaremos un histograma, como el
que se muestra.

6. Datos agrupados
1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 81 52 81 64 83 79 77 74 79 70 77 77 62 67 81
2 71 68 71 85 65 91 51 61 80 82 63 91 71 74 78
3 86 65 66 56 73 75 83 62 70 60 68 86 66 83 75
4 67 45 78 77 83 65 89 54 60 69 75 66 73 72 68
5 86 76 48 66 67 74 58 70 60 49 88 56 68 90 75
6 74 70 85 73 76 66 72 87 69 70 66 70 55 88 70
7 71 80 70 75 76 69 71 77 72 63 64 56 57 66 80
8 75 74 90 89 81 64 62 91 61 62 64 58 72 69 59
9 75 71 79 86 74 74 75 81 67 97 54 73 80 63 70
10 63 67 49 100 66 79 71 77 75 60 66 58 72 57 60

7. Datos agrupados
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
62 67 79 71 79 65 70 84 62 73 87 65 72 65 92
72 59 60 66 63 83 65 87 62 79 89 51 70 70 56
54 62 82 78 64 76 71 71 73 53 68 85 77 68 72
67 77 42 80 68 64 73 55 79 43 58 74 78 79 57
67 66 75 77 66 73 76 70 54 90 61 62 90 81 81
66 83 69 72 65 85 74 79 59 72 78 67 81 77 57
78 54 77 77 79 75 75 62 73 80 53 89 59 67 78
81 65 62 63 85 68 74 75 61 60 62 50 94 77 91
65 80 73 81 50 75 89 71 59 79 83 80 92 69 57
75 69 60 73 62 83 72 66 85 61 52 86 55 83 80

8. Datos agrupados
Primer paso:
Encontrar en los datos el valor máximo y el mínimo
para calcular el rango.
Valor máximo = 100
Valor mínimo = 42
Rango = 100 – 42
Rango = 58
1 1 2 3 4 5 6 7 8 9 10
1 81 52 81 64 83 79 77 74 79 70
2 71 68 71 85 65 91 51 61 80 82
3 86 65 66 56 73 75 83 62 70 60
4 67 45 78 77 83 65 89 54 60 69
5 86 76 48 66 67 74 58 70 60 49
6 74 70 85 73 76 66 72 87 69 70
7 71 80 70 75 76 69 71 77 72 63
8 75 74 90 89 81 64 62 91 61 62
9 75 71 79 86 74 74 75 81 67 97
10 63 67 49 100 66 79 71 77 75 60
16 17 18 19 20 21
62 67 79 71 79 65
72 59 60 66 63 83
54 62 82 78 64 76
67 77 42 80 68 64
67 66 75 77 66 73
66 83 69 72 65 85
78 54 77 77 79 75
81 65 62 63 85 68
65 80 73 81 50 75
75 69 60 73 62 83

9. Datos agrupados
Segundo paso:
Determinar el número de intervalos en que se van a
agrupar los datos. Existen varias formas:
El número de intervalos se puede calcular
obteniendo la raíz cuadrada del número de datos:
Se tomarían 17 ó 18 intervalos
Pero en este caso no lo haremos.
300 17.3205

10. Datos agrupados
Segundo paso:
El número de intervalos se puede calcular
obteniendo la raíz cuadrada del número de datos:
Se tomarían 17 ó 18 intervalos
Otra forma consiste en establecer arbitrariamente
el número de intervalos.
En este caso, de acuerdo con las indicaciones,
vamos a fijarlo en 10
300 17.3205

11. Datos agrupados
Tercer paso:
Determinar el tamaño del intervalo
Se divide el rango entre el número de intervalos:
Como los datos son enteros, se toma un tamaño de
intervalo también entero, podría ser 5 ó 6. Vamos a
tomar el 5 y veamos cómo quedan los intervalos.
58
5.8
10


12. Datos agrupados
Cuarto paso:
Construir los 10 intervalos aparentes.
Existen muchas formas de llevar a cabo este paso
debido a que son sólo operaciones aritméticas,
vamos a ver una de ellas.
Se elige un valor inicial para que sea el primer
límite inferior. Debe ser menor o igual al valor
mínimo (el valor mínimo es 42).
Por lo tanto, vamos a elegir el 40 como valor inicial.

13. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40
2
3
4
5
6
7
8
9
10
Este valor inicial debe ser menor o
igual al mínimo; pudo haberse
elegido 39, 40, 41, 42, etcétera.
Posteriormente puede cambiarse en
caso necesario.

14. Datos agrupados
Cuarto paso:
A partir de este valor inicial (40) se calculan los 10
límites inferiores.
Se va sumando a cada límite, el tamaño del
intervalo, como se muestra en la siguiente
diapositiva.

15. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40
2 45
3 50
4 55
5 60
6 65
7 70
8 75
9 80
10 85
Vamos a ir sumando el
tamaño del intervalo:
40 + 5 = 45
45 + 5 = 50
…
+5
+5
+5

16. Datos agrupados
Cuarto paso:
Antes de continuar debemos revisar que el último
límite inferior (el décimo límite inferior, ya que
fijamos en 10 el número de intervalos) sea menor o
igual al valor máximo (100).
Observa en la siguiente diapositiva que el décimo
límite inferior es igual a 85.

17. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40
2 45
3 50
4 55
5 60
6 65
7 70
8 75
9 80
10 85
Este límite debe ser:
Menor o igual
Al valor máximo
85 ≤ 100

18. Datos agrupados
Cuarto paso:
Ahora vamos a obtener el primer límite superior.
Como los datos son enteros se le resta un entero al
segundo límite inferior:
Segundo límite inferior = 45
Menos un entero = 44
El primer límite superior será 44

19. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 44
2 45
3 50
4 55
5 60
6 65
7 70
8 75
9 80
10 85
45 – 1 = 44
Se resta un entero
porque los datos son
enteros; si tienen un
decimal se resta 0.1 y si
tiene dos, se resta 0.01

20. Datos agrupados
Cuarto paso:
Finalmente, vamos a sumar el tamaño del intervalo
a cada límite superior en forma similar a lo que se
llevó a cabo con los límites inferiores.
44 + 5 = 49
49 + 5 = 54
…

21. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 44
2 45 49
3 50 54
4 55 59
5 60 64
6 65 69
7 70 74
8 75 79
9 80 84
10 85 89
Vamos a ir
sumando el
tamaño del
intervalo:
44 + 5 = 49
49 + 5 = 54
…
+5
+5
+5

22. Datos agrupados
Cuarto paso:
Ya están calculados los intervalos, sin embargo,
debemos revisar que se cumplan otras dos
condiciones:
El primer límite superior debe ser mayor o igual al
valor mínimo (42).
El último límite superior debe ser mayor o igual al
valor máximo (100)

23. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 44
2 45 49
3 50 54
4 55 59
5 60 64
6 65 69
7 70 74
8 75 79
9 80 84
10 85 89
Este valor debe
ser mayor o igual
al valor mínimo:
44 ≥ 42
Este valor debe
ser mayor o igual
al valor máximo:
89 ≥ 100 ???

24. Datos agrupados
Cuarto paso:
Una de las condiciones necesarias para continuar
con el procedimiento no se cumplió, debemos
cambiar alguno de los siguientes valores:
El primer límite inferior
El tamaño del intervalo
El número de intervalos
Ajustando estos valores trataremos de obtener 10
intervalos de tal modo que se cumplan las 4
condiciones.

25. Datos agrupados
Cuarto paso:
Si cambiamos el primer límite inferior:
Sólo podemos aumentarlo en dos unidades: Tomar
como valor inicial 42.
Esto aumentaría el último límite superior en dos
unidades: 89 + 2 = 91
No es suficiente, ya que de cualquier modo, no se
cumple la condición de que el último límite superior
debe ser mayor o igual al máximo.

26. Datos agrupados
Cuarto paso:
Estamos tratando de obtener 10 intervalos pero
cumpliendo las 4 condiciones.
Lo intentamos cambiando el valor inicial, pero no
funcionó
Veamos que pasa si cambiamos el tamaño del
intervalo:
Necesitamos un tamaño de intervalo más grande
para que el último límite superior aumente lo
suficiente para que sea mayor que el valor máximo.
Vamos a probar con un tamaño de intervalo igual a 6.

27. Datos agrupados
Cuarto paso:
No olvidemos que:
Si aumentar el valor inicial no es suficiente y
aumentar el tamaño del intervalo tampoco cumple
todas las condiciones.
Nos quedaría como último recurso cambiar el
número de intervalos.
Pero antes de cambiar el número de intervalos
vamos a ver qué sucede al aumentar el tamaño del
intervalo.

28. Datos agrupados
Cuarto paso:
Veamos como queda la tabla si tomamos como
tamaño del intervalo el 6.
El primer límite inferior será igual a 40.
Observa la construcción de la tabla en las
siguientes diapositivas.

29. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40
2
3
4
5
6
7
8
9
10
Este valor inicial debe ser menor o
igual al mínimo; pudo haberse
elegido 39, 40, 41 ó 42 .
Posteriormente puede cambiarse en
caso necesario.

30. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40
2 46
3 52
4 58
5 64
6 70
7 76
8 82
9 88
10 94
Vamos a ir sumando el
tamaño del intervalo:
40 + 6 = 46
46 + 6 = 52
…
+6
+6
+6

31. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40
2 46
3 52
4 58
5 64
6 70
7 76
8 82
9 88
10 94
Este límite debe ser:
Menor o igual
Al valor máximo
94 ≤ 100
Es correcto.
+6
+6
+6

32. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 45
2 46
3 52
4 58
5 64
6 70
7 76
8 82
9 88
10 94
46 – 1 = 45

33. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 45
2 46 51
3 52 57
4 58 63
5 64 69
6 70 75
7 76 81
8 82 87
9 88 93
10 94 99
Vamos a ir
sumando el
tamaño del
intervalo:
45 + 6 = 51
51 + 6 = 57
…
+6
+6
+6

34. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 45
2 46 51
3 52 57
4 58 63
5 64 69
6 70 75
7 76 81
8 82 87
9 88 93
10 94 99
Este valor debe
ser mayor o igual
al valor mínimo:
45 ≥ 42
Este valor debe
ser mayor o igual
al valor máximo:
99 ≥ 100 (?)

35. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 40 45
2 46 51
3 52 57
4 58 63
5 64 69
6 70 75
7 76 81
8 82 87
9 88 93
10 94 99
99 ≥ 100 (?)
No cumple con la
condición de ser
mayor o al menos
igual al máximo.

36. Datos agrupados
Cuarto paso:
Todavía no terminamos el cuarto paso, a veces es
necesario realizar varios ajustes antes de obtener
los intervalos apropiados.
En este caso sólo es necesario aumentar el valor
inicial una unidad, aumentarlo de 40 a 41.
Al aumentar una unidad el valor inicial, todos los
valores aumentan en esa misma unidad, de modo
que el último límite superior será 100, como se
muestra en la siguiente diapositiva.

37. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 41 46
2 47 52
3 53 58
4 59 64
5 65 70
6 71 76
7 77 82
8 83 88
9 89 94
10 95 100
Los cuatro valores
cumplen con las
condiciones
necesarias.

38. Datos agrupados
Intervalo
número
Intervalos aparentes
Límites inferiores Límites superiores
1 41 46
2 47 52
3 53 58
4 59 64
5 65 70
6 71 76
7 77 82
8 83 88
9 89 94
10 95 100
Los cuatro valores
cumplen con las
condiciones
necesarias.

39. Datos agrupados
Cuarto paso:
Finalmente hemos obtenido los intervalos
aparentes.
Estos intervalos son útiles para contar los datos
cuando hay que hacerlo manualmente, pero en la
tabla deben anotarse los intervalos reales.
En la siguiente presentación continuaremos con el
paso 5: Obtener intervalos reales.

40. Gracias por su atención
licmata@hotmail.com
http://licmata-math.blogspot.com/
http://www.scoop.it/t/mathematics-learning
http://www.slideshare.net/licmata/
http://www.facebook.com/licemata
Twitter: @licemata