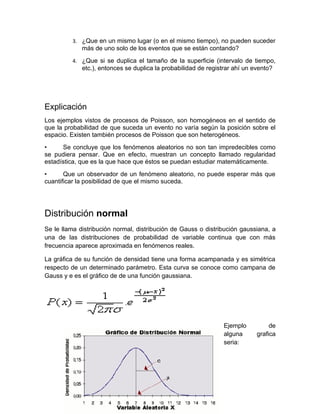
El documento resume varias distribuciones de probabilidad importantes como la distribución de Bernoulli, la distribución binomial, la distribución de Poisson, la distribución normal, la distribución gamma y la distribución t-student. Para cada distribución, se define brevemente y se proporciona un ejemplo ilustrativo. El documento explica cuándo es apropiado usar cada distribución y cómo modelar diferentes tipos de fenómenos aleatorios.

1. Procesos industriales área manufactura.
Estadística.
Distribuciones de probabilidad.
Leonardo García Lamas.
Grupo y sección: 2 “a”

2. DISTRIBUCIÓN DE BERNOULLI
En teoría de probabilidad y estadística, la distribución de Bernoulli (o distribución
dicotómica), nombrada así por el matemático y científico suizo Jakob Bernoulli, es
una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de
éxito p y valor 0 para la probabilidad de fracaso q = 1 − p. Por lo tanto, si X es una
variable aleatoria con esta distribución.
Consiste en realizar un experimento aleatorio una sola vez y observar si cierto
suceso ocurre o no, siendo p la probabilidad de que esto sea así (éxito) y q=1-p el
que no lo sea (fracaso).
Explicación
Un experimento que tenga dos resultados. Al primero se le llama éxito y al otro
fracaso. La probabilidad por éxito se denota por p. por consecuencia la
probabilidad de fracaso es 1-p. lo anterior representa un ensayo de Bernoulli con
probabilidad de éxito p. el mas el mas sencillo de este es el lanzamiento de una
moneda. Los posibles resultados son dos “cara o cruz” si cara se define como
éxito, entonces p constituye esa probabilidad. En una moneda p= ½
N=número de elementos.
P=éxito.
q=fracaso.
X=variable aleatoria.
La distribución Bernoulli estada por los únicos dos valores posibles que deben ser
1 y 0; de no cumplirse esta regla es decir si se quebranta se estaría ablando de
que no es una distribución Bernoulli sino otra de las tantas distribuciones.
Ejemplo:
X p
1 .5
0 .5
Suma 1

3. Distribución binomial
La distribución binomial esta asociada a experimentos del siguiente tipo:
- Realizamos n veces cierto experimento en el que consideramos solo la
posibilidad de éxito o fracaso.
- La obtención de éxito o fracaso en cada ocasión es independiente de la
obtención de éxito o Fracaso en las demás ocasiones.
- La probabilidad de obtener ´éxito o fracaso siempre es la misma en cada
ocasión.
Explicación
Tiramos un dado 7 veces y contamos el numero de cincos que obtenemos. ¿Cual
es la probabilidad de obtener tres cincos?.
Este es un típico ejemplo de distribución binomial, pues estamos repitiendo 7
veces el experimento de lanzar un dado. ¿Cual es nuestro éxito?
Evidentemente, sacar un 5, que es en lo que nos fijamos.
El fracaso, por tanto, seria no sacar 5, sino sacar cualquier otro número.
Por tanto, Éxito = E = “sacar un 5” =⇒p (E) =
1
6
Fracaso = F = “no sacar un 5” =⇒p (F) =
5
6
Para calcular la probabilidad que nos piden, observemos que nos dicen que
sacamos 3 cincos y por lo tanto tenemos 3 ´éxitos y 4 fracasos, ¿de cuantas
maneras pueden darse estas posibilidades?

4. Podríamos sacar 3 cincos en las 3 primeras tiradas y luego 4 tiradas sin sacar
cinco, es decir: EEEFFFF
Pero también podríamos sacar EFEFFFE, es decir que en realidad estamos
calculando la E es éxito y la F es fracaso.
Distribución de Poisson
En teoría de probabilidad y estadística, la distribución de Poisson es una
distribución de probabilidad discreta que expresa, a partir de una frecuencia de
ocurrencia media, la probabilidad que ocurra un determinado número de eventos
durante cierto periodo de tiempo.
La función de masa de la distribución de Poisson es
Donde
• k es el número de ocurrencias del evento o fenómeno (la función nos
da la probabilidad de que el evento suceda precisamente k veces).
• λ es un parámetro positivo que representa el número de veces que se
espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el
suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos
interesados en la probabilidad de que ocurra k veces dentro de un intervalo
de 10 minutos, usaremos un modelo de distribución de Poisson con λ =
10×4 = 40.
• e es la base de los logaritmos naturales (e = 2,71828 ...)
Tanto el valor esperado como la varianza de una variable aleatoria con distribución
de Poisson son iguales a λ. Los momentos de orden superior son polinomios de
Touchard en λ cuyos coeficientes tienen una interpretación combinatorio. De
hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces
según la fórmula de Dobinski, el n-ésimo momento iguala al número de particiones
de tamaño n.
La moda de una variable aleatoria de distribución de Poisson con un λ no entero
es igual a , el mayor de los enteros menores que λ (los símbolos representan
la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de la distribución de Poisson con valor
esperado λ es

5. Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente
divisibles.
La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de
parámetro λ0 a otra de parámetro λ es
¿Para qué sirve conocer que algo es Poisson?
Porque si se tiene caracterizado el comportamiento probabilístico de un fenómeno
aleatorio, podemos contestar preguntas como:
1. ¿Qué probabilidad hay de que lleguen más de 15 clientes al banco
en un intervalo de 5 minutos de duración?
2. ¿Qué probabilidad hay de que suceda por lo menos una falla en un
tramo de 1km de tubería de gas?
3. ¿Qué probabilidad hay de que en un estanque de cultivo de
camarón, haya más de media tonelada?
4. ¿Qué probabilidad hay de que en un área de 1km se encuentren
más de 3 brotes de una enfermedad?
¿Por qué algunas cosas supimos de antemano que iban a ser Poisson y que otras
no?
Porque los fenómenos que son procesos de Poisson en la línea o en el tiempo, en
la superficie, o en el espacio, tienen algunas características que matemáticamente
la delatan, como son:
1. ¿Que se está contando el número de eventos que suceden en un
área (o intervalo de tiempo, o volumen) determinada?
2. ¿Que la probabilidad de que suceda un evento sobre un área muy
pequeña, es también muy pequeña?

6. 3. ¿Que en un mismo lugar (o en el mismo tiempo), no pueden suceder
más de uno solo de los eventos que se están contando?
4. ¿Que si se duplica el tamaño de la superficie (intervalo de tiempo,
etc.), entonces se duplica la probabilidad de registrar ahí un evento?
Explicación
Los ejemplos vistos de procesos de Poisson, son homogéneos en el sentido de
que la probabilidad de que suceda un evento no varía según la posición sobre el
espacio. Existen también procesos de Poisson que son heterogéneos.
• Se concluye que los fenómenos aleatorios no son tan impredecibles como
se pudiera pensar. Que en efecto, muestran un concepto llamado regularidad
estadística, que es la que hace que éstos se puedan estudiar matemáticamente.
• Que un observador de un fenómeno aleatorio, no puede esperar más que
cuantificar la posibilidad de que el mismo suceda.
Distribución normal
Se le llama distribución normal, distribución de Gauss o distribución gaussiana, a
una de las distribuciones de probabilidad de variable continua que con más
frecuencia aparece aproximada en fenómenos reales.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica
respecto de un determinado parámetro. Esta curva se conoce como campana de
Gauss y e es el gráfico de de una función gaussiana.
Ejemplo de
alguna grafica
seria:

7. Distribución gamma
Es una distribución adecuada para modelizar el comportamiento de variables
aleatorias continuas con asimetría positiva. Es decir, variables que presentan una
mayor densidad de sucesos a la izquierda de la media que a la derecha. En su
expresión se encuentran dos parámetros, siempre positivos, (α) alfa y (β) beta de
los que depende su forma y alcance por la derecha, y también la función Gamma
Γ (α), responsable de la convergencia de la distribución.
Los parámetros de la distribución
El primer parámetro (α) sitúa la máxima intensidad de probabilidad y por este
motivo en algunas fuentes se denomina “la forma” de la distribución: cuando se
toman valores próximos a cero aparece entonces un dibujo muy similar al de la
distribución exponencial. Cuando se toman valores más grandes de (α) el centro
de la distribución se desplaza a la derecha y va apareciendo la forma de una
campana de Gauss con asimetría positiva.
Es el segundo parámetro (β) el que determina la forma o alcance de esta
asimetría positiva desplazando la densidad de probabilidad en la cola de la
derecha. Para valores elevados de (β) la distribución acumula más densidad de
probabilidad en el extremo derecho de la cola, alargando mucho su dibujo y
dispersando la probabilidad a lo largo del plano. Al dispersar la probabilidad la
altura máxima de densidad de probabilidad se va reduciendo; de aquí que se le
denomine “escala”. Valores más pequeños de (β) conducen a una figura más
simétrica y concentrada, con un pico de densidad de probabilidad más elevado.
Una forma de interpretar (β) es “tiempo promedio entre ocurrencia de un suceso”.
Relacionándose con el parámetro de la Poisson como β=1/λ. Alternativamente λ
será el ratio de ocurrencia: λ=1/β. La expresión también será necesaria más
adelante para poder llevar a cabo el desarrollo matemático.
Explicación

8. La distribución gamma se puede caracterizar del modo siguiente: si se está
interesado en la ocurrencia de un evento generado por un proceso de Poisson de
media lambda, la variable que mide el tiempo transcurrido hasta obtener n
ocurrencias del evento sigue una distribución gamma con parámetros a=n×lambda
(escala) y p=n (forma). Se denota Gamma(a,p).
Por ejemplo, la distribución gamma aparece cuando se realiza el estudio de la
duración de elementos físicos (tiempo de vida).
Distribución t- student
En probabilidad y estadística, la distribución t (de Student) es una distribución de
probabilidad que surge del problema de estimar la media de una
población normalmente distribuida cuando el tamaño de la muestra es pequeño.
Aparece de manera natural al realizar la prueba t de Student para la determinación
de las diferencias entre dos medias muéstrales y para la construcción
del intervalo de confianza para la diferencia entre las medias de dos poblaciones
cuando se desconoce la desviación típica de una población y ésta debe ser
estimada a partir de los datos de una muestra.
Explicación
Es una distribución de probabilidad que surge del problema de estimar la media
de una población normalmente distribuida cuando el tamaño de la muestra es
pequeño.
Aparece de manera natural al realizar la prueba t de Student para la determinación
de las diferencias entre dos medias muéstrales y para la construcción del intervalo
de confianza para la diferencia entre las medias de dos poblaciones cuando se
desconoce la desviación típica de una población y ésta debe ser estimada a partir
de los datos de una muestra.