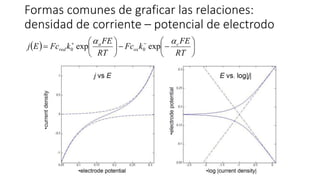
El documento presenta conceptos básicos de cinética electroquímica, incluyendo densidad de corriente, sobrepotencial, curvas de polarización, teoría de complejos activados y ecuaciones que relacionan el potencial y la densidad de corriente en un electrodo. Explica cómo la densidad de corriente depende exponencialmente del sobrepotencial según la ecuación de Butler-Volmer.

1. Introducción a la
Electroquímica
UMSA – Febrero, 2015
Grupo Baterías IGN-IIQ
Lección 2

2. Cinética del electrodo
• Perdidas en una celda electroquímica durante su operación
• Densidad de corriente, sobrepotencial
• Curvas de polarización
• Teoría de complejos activados
• Dependencia entre potencial y energía de activación
• Ecuaciones básicas de la cinética de electrodos

3. Cinética del electrodo
No existe “caída” IR
No existe sobrepotencial
Existe IR-drop y sobrepoentiales η, V

d
iIR 
Conductividad del electrolito κ [S/m]

4. Componentes del potencial Ecelda
celda
Aniones
Ánodo
Cationes
Cátodo
celda

5. Perdidas en una celda electroquímica durante
operación (galvánica o electrolítica?)
Voltaje de circuito abierto
Perdida IR
Polarización por Activación
Polarización por concentración
Voltaje de
operación
Incremento de corriente
Incrementodelvoltajedelacelda
Polarización de una celda como función de la corriente de operación

6. Sub-Procesos en la reacción de electrodo
Como se necesitan fuerzas impulsoras para llevar adelante los sub-procesos, entonces Ecell ≠ Eeq

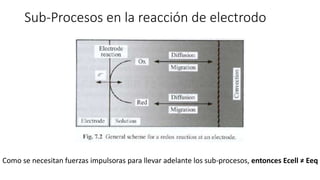
7. Densidad de corriente y sobrepotencial
• Velocidad de reacción química heterogénea: J [mol m-2 s-1]
También es valida para reacciones electroquímicas!
• Densidad de corriente: j = nFJ [(As mol-1)*(mol m-2 s-1)=A m-2]
• Como varia el voltaje de la celda y el potencial del electrodo con respecto a la densidad de
corriente?
• Sobrepotencial en el electrodo: (=Fuerza impulsora para el proceso)
• η y j son positivos para Corrientes anódicas y negativos para Corrientes catódicas
Potencialdeelectrodo
Corriente
Esquemáticamente tenemos:
rEE 

8. Curva de polarización para la evolución de H2
• Experimento realizado por Tafel en 1905
• Válido para |η| relativamente altos (>0.1 V)
• Ecuación de Tafel:
• Comparación con la ecuación de Arrehnius:
para una velocidad de reacción J = k*c
Bconstj  .log
RT
E
constk a
 .ln

9. • Etapas del proceso de una reacción química
a través de complejos activados
• Velocidad de reacción (hacia la derecha)
• Constante de velocidad de reacción (hacia la
derecha)
Donde ∆Gf es la energía de activación
• La velocidad de reacción será entonces:
•
Teoría de complejos activados
  ABABBA 

BAff cckJ 







 


RT
G
kk
f
ff exp0







 


RT
G
cckJ
f
BAff exp0

10. • Empezamos observando la reacción
anódica (+)
• Que pasa con ∆Gf cuando E se varia
de E1 a E2?
• ϕM varia respecto a ϕS
• La energía de 1 mol de electrons en el
metal cambia en el orden de:
-F(E2-E1)
• Las especies Ox y Red no son afectadas
Energía involucrada en una reacción química
REDOX
     1212 EEFEGEG  

11. Sobrepotencial de activación
 





 



RT
G
kFcj
FGG
FGG
r
i
cc
aa
#
0
#
,1
#
,2
#
,1
#
,2
exp
1


∆ϕ = (E2 – E1) es positivo, signo opuesto
al cambio en energía libre

12. Relación entre j y E
Para una corriente parcial anódica (asumiendo E1 = 0, E2 = E)
 
     





 







 

RT
FE
kFc
RT
FEEG
kFcEj a
red
aa
reda
 1
exp
10
exp 0
#
1,'
0
Análogamente para una corriente parcial catódica
 
 













 

RT
FE
kFc
RT
FEEG
kFcEj c
ox
cc
oxc

exp
0
exp 0
#
1,'
0
Las corrientes catódicas y las velocidades de reacción son negativos por definición!
Por lo tanto la densidad de corriente neta es:
   











 

RT
FE
kFc
RT
FE
kFcjjEj c
ox
a
redca

exp
1
exp '
0
'
0

13. Relación entre j y E, gráficamente
   











 
 
RT
FE
kFc
RT
FE
kFcEj oxred

exp
1
exp 00
OJO: j = 0 en el potencial de
equilibrio

14. Influencia de β
   











 
 
RT
FE
kFc
RT
FE
kFcEj oxred

exp
1
exp 00
β = 0.4

15. Para reacciones multielectron (n ≥ 2)
• Se procede en series de transferencias de un electrón: j=nFJ
• β se reemplaza por nβ; (1- β) se reemplaza por n(1- β)
• β depende de cual sera el paso determinante de la velocidad
• Notación alternativa:
  nnn caca   ;;1

16. La densidad de corriente de intercambio
• Al potencial de equilibrio Er, ambas reacciones proceden a la misma velocidad:
      0  rrr EjEjEj     0jEjEj rr  
Donde j0 es la densidad de corriente de intercambio
• Al potencial reposo se tendrá:
  











 
RT
FE
knFc
RT
FE
knFcEj rc
ox
ra
red

expexp 000
• Reordenando se obtiene:












 

red
ox
r
c
c
nF
RT
k
k
nF
RT
E lnln
0
0
• Este resultado es consistente con la ecuación de Nernst?

17. Formas comunes de graficar las relaciones:
densidad de corriente – potencial de electrodo
  











 
RT
FE
kFc
RT
FE
kFcEj c
ox
a
red

expexp 00

18. La ecuación Butler – Volmer: j vs η
• Escribiendo el potencial del electrodo como E = Er + η
• Y para el catodo
• La corriente neta es:
Ecuación de Butler – Volmer!!
  










 
 

RT
F
j
RT
FFE
knFcEj aara
red

expexp 00
  










 
 

RT
F
j
RT
FFE
knFcEj ccrc
red

expexp 00
 



















RT
F
RT
F
jj ca 
 expexp0