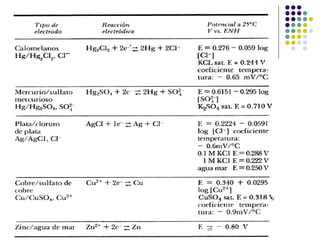
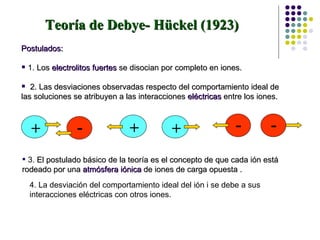
Electroquímica industrial

TEMA 1.- INTRODUCCIÓN A LA INGENIERÍA ELECTROQUÍMICA Se centra en el diseño, caracterización y operación de componentes, montajes y procesos que impliquen la interconversión de energía química y eléctrica Abarca : Procesos electroquímicos Sistemas de procesado ( reactor electroquímico ) Productos resultantes Aplicación a un fin útil Su ámbito es la explotación práctica de una ciencia interdisciplinar mediante la aplicación de métodos ingenieriles La escala de operaciones va desde estudios en laboratorio con microelectrodos hasta procesos a escala total

Áreas de aplicación Electrosíntesis de compuestos orgánicos, inorgánicos, semiconductores… Estabilidad de materiales y procesado . Grabado de metales, recubrimientos… Conversión de potencia eléctrica : Células de combustible, baterías… Técnicas de protección medioambiental : Purificación de aguas… Aplicaciones biomédicas

Conceptos y Unidades Básicas Potencial de electrodo : Cuando un material conductor se pone en contacto con una disolución electrolítica se produce espontáneamente una d.d.p. eléctrica en la interfase electrodo-disolución. Tal diferencia se denomina potencial de electrodo y se mide en voltios (v). Representa el trabajo que hay que realizar para desplazar la unidad de carga eléctrica entre los dos extremos de la interfase. Los potenciales se miden frente a un electrodo de referencia, y pueden modificarse mediante la imposición de un potencial externo a través de una fuente de alimentación ELECTRODOS DE REFERENCIA 2H + + 2e -  H 2 Electrodo de hidógeno standard (EHS) Hg 2 Cl 2 + 2e -  2 Hg +2 Cl - . Electrodo de calomelanos saturado (ECS) AgCl + e-  Ag + Cl - Electrodo de plata/cloruro de plata Cu  Cu 2+ + 2e - Electrodo de cobre/sulftato de cobre

Voltaje.- El voltaje de una celda es la diferencia de potencial, en voltios, entre los dos electrodos extremos. Es la suma de varias contribuciones : * Potencial de equilibrio del ánodo * Potencial de equilibrio del cátodo * Sobrevoltajes * Caída óhmica en el o los electrolitos Intensidad.- Es el flujo de electrones que circulan por el circuito eléctrico en la unidad de tiempo. Se mide en amperios (A). La velocidad de un proceso electroquímico es directamente proporcional a la intensidad de corriente Densidad de corriente .- Es la intensidad por unidad de área efectiva de electrodo. Se mide en amperios/m 2. Es un parámetro de suma importancia puesto que de él dependen: * La velocidad del proceso * La selectividad * La eficacia de la corriente * El consumo específico de energía * La velocidad de corrosión de un electrodo

Resistencia eléctrica .- Es la oposición que presenta todo conductor al paso de la corriente y se mide en ohmios (  ). El término I.R se denomina caída óhmica. Resistividad .- Representa la resistencia específica de un material de 1 cm de Longitud y 1 cm 2 de sección transversal. Es función de la temperatura y de la naturaleza del material Conductividad .- Es el inverso de la resistividad. Se mide en Siemens/cm 1 S = 1  -1 . Todas las partes por las que circula la corriente deben tener una alta Conductividad Eficacia de la corriente .- Es la fracción de corriente, que, siguiendo la ley de Faraday, se utiliza en la obtención del producto deseado, en su destrucción o en el transporte Rendimiento espacio-tiempo .- Es la cantidad de producto obtenido o el caudal tratado por unidad de tiempo y de volumen de celda. Es función de la densidad de corriente, de la eficacia de la misma y del área de electrodo por unidad de volumen

Consumo específico de energía .- Es el consumo de energía eléctrica por cantidad de producto producido o destruido. Es de suma importancia para decidir la viabilidad de un proceso. Viene dado por la expresión : CE = (26,8 n E t ) / ( E c M) n = nº de electrones intercambiados por mol de producto E t = voltaje total de la celda E c = Eficacia de la corriente M = peso molecular del producto Tiempo de residencia .- Es el tiempo que precisa un elemento infinitesimal de volumen de electrolito en pasar a través de la celda una sola vez t r = l S / Q Conductancia .- Se denomina conductancia (G) a la inversa de la resistencia eléctrica. La unidad es el ohm -1 , mho, o Siemens. Las medidas realizadas por F.W. Kohlrausch en 1894 de conductancia molar para diferentes electrolitos mostraron dos tipos de comportamiento. Los mismos se muestran en la siguiente gráfica:

Por un lado, los electrolitos verdaderos (fuertes), como el KCl, el HCl, etc., muestran una disminución lineal de la conductancia molar con la raíz cuadrada de la concentración. Por otro lado, los electrolitos potenciales (débiles), como el ácido acético, sulfato de níquel, el agua, etc., muestran valores máximos de conductancia molar cuando C  0 (dilución infinita), pero disminuyen rápidamente a valores bajos cuando aumenta la concentración. Kohlrausch demostró que : donde  o es la conductancia molar límite y A un coeficiente que depende de la naturaleza del electrolito, del disolvente y de la temperatura Kohlrausch también demostró que  0 , para cualquier electrolito, se puede expresar como la suma de las contribuciones de las conductancias iónicas de cada una de las especies constituyentes . ; pero la ley de Kohlrausch no suministra, la forma de calcular las contribuciones individuales de los diferentes iones, solo permite evaluar variaciones (  ).

Teoría de Debye- Hückel (1923) Postulados: 1. Los electrolitos fuertes se disocian por completo en iones. 2. Las desviaciones observadas respecto del comportamiento ideal de las soluciones se atribuyen a las interacciones eléctricas entre los iones. 3. El postulado básico de la teoría es el concepto de que cada ión está rodeado por una atmósfera iónica de iones de carga opuesta . 4. La desviación del comportamiento ideal del ión i se debe a sus interacciones eléctricas con otros iones. - + + + - -

5. La desviación se expresa como diferencia de potencial químico   i (ideal) =  ° i + RT ln c i  i (real) =  ° i + RT ln a i =  °i + RT ln c i + RT ln  i   i = RT ln a i - RT ln c i = RT ln  i : potencial eléctrico derivado del ión central i z i : número de carga del ión i e c : carga del electrón  : constante dieléctrica en el vacio (o) y del solvente (r) r: radio de influencia de i b: distancia (radio) de Debye-Huckel (atmósfera iónica) Permite calcular el trabajo eléctrico de introducir una carga eléctrica en el radio de influencia del ión central i El trabajo eléctrico (potencial x carga;  .z i .e c es igual a la diferencia de potencial químico (RT ln  i )  .z i .e c = RT ln  i Ecuación de Debye-Hückel

Reacciones Electroquímicas Son reacciones químicas heterogéneas con transferencia de carga a través de la interfase entre un electrodo y un electrolito. Los componentes mínimos son : un ánodo, un cátodo, contacto iónico entre los electrodos (via electrolito) y un contacto electrónico entre ellos (circuito eléctrico externo) En el cátodo se produce una reducción de las especies por ganancia de electrones, mientras que en el ánodo se produce la oxidación.

Reacciones Electroquímicas Las reacciones electroquímicas implican fases sólidas, líquidas y gaseosas y, a menudo, implican cambios de fase : desprendimientos gaseosos, electrodeposiciones de metales, disoluciones de metales, etc Frecuentemente, participa el disolvente Los protones (hidratados) y los iones hidroxilos, a menudo, intervienen, por lo que hay una dependencia con el pH Algunas reacciones implican contacto entre tres fases En otras, el material electródico activo se aplica como un recubrimiento superficial, en vez de utilizarlo como un material en bloque Un mismo producto se puede obtener por vías electroquímicas diferentes El electrodo puede, él mismo, ser un reactivo Es importante considerar la posibilidad de formación de complejos Algunas reacciones electroquímicas pueden ser reversibles

Reacciones Electroquímicas Queda claro que las reacciones electroquímicas implican gran variedad de especies, y diferentes tipos de materiales electródicos. Los reactivos y productos pueden ser : Inorgánicos, orgánicos o bioquímicos Sólidos, líquidos o gaseosos De base electródica o electrolítica Neutros, cargados positivamente o negativamente Solubles o insolubles Por su parte, la reacción electroquímica puede ser : Oxidación anódica o reducción catódica Proceso deliberado o involuntario Un medio para síntesis, recubrimiento, retirada de especies tóxicas, detectar o seguir una especie, o almacenamiento o conversión de energía El electrodo activo puede ser : Metal, carbón, polímero, …

Reacciones Electroquímicas Las especies reaccionantes deben estar localizadas a distancias moleculares de la superficie del electrodo, por lo que el progreso de una reacción dependerá del adecuado aporte de reactivo a la superficie del electrodo y la retirada de producto de ella, además de la transferencia de carga en la interfase electrodo/electrolito O + ne -  R 1ª etapa O seno  O electrodo 2ª etapa O electrodo + ne -  R electrodo 3ª etapa R electrodo  R seno La velocidad de la etapa más lenta determinará la velocidad global Pero hay otros factores que habrá que tener en cuenta en la reacción electroquímica

Reacciones electroquímicas Formación de fase en la superficie electródica. Nucleación de una nueva fase que luego irá creciendo Reacciones químicas puras Adsorción en la superficie del electrodo Transferencia electrónica múltiple En todo proceso se hace necesario medir el potencial del electrodo de trabajo frente a un electrodo de referencia utilizando un voltímetro digital. Las siguientes tablas muestran la serie electroquímica de potenciales para distintos pares medidos frente al electrodo de hidrógeno

+2,865 F 2 + 2 e  = 2F  F  | F 2 (Pt) +1,808 Co 3+ + e  = Co 2+ Co 3+ , Co 2+ |Pt +1,693 Pb 4+ + 2 e  = Pb 2+ Pb 4+ , Pb 2+ |Pt +1,691 Au + + e  = Au Au + |Au +1,507 MnO 4  +8H + + 5 e  = Mn 2+ + 4H 2 O MnO 4  , H + , Mn 2+ |Pt +1,497 Au 3+ + 3 e  = Au Au 3+ |Au +1,359 Cl 2 + 2 e  = 2Cl  Cl  |Cl 2 (Pt) +1,333 Cr 2 O 7 2  + 14 H + + 6 e  = 2Cr 3+ + 7H 2 O Cr 2 O 7 2  , H + ,Cr 3+ | Pt +1,252 Tl 3+ + 2 e  = Tl + Tl 3+ ,Tl + | Pt +1,229 O 2 + 4H + + 4 e  = 2H 2 O H + |O 2 (Pt) +1,066 Br 2 + 2 e  = 2Br  Br  |Br 2 (Pt) +0,919 2Hg 2+ + 2 e  = Hg 2 2+ Hg 2+ , Hg 2 2+ | Pt +0,854 Hg 2+ + 2 e  = Hg Hg 2+ |Hg +0,799 Ag + + e  = Ag Ag + |Ag +0,788 Hg 2 2+ + 2 e  = 2Hg Hg 2 2+ |Hg +0,770 Fe 3+ + e  = Fe 2+ Fe 3+ , Fe 2+ |Pt +0,535 I 2 + 2 e  = 2I  I  |I 2 (Pt) +0,520 Cu + + e  = Cu Cu + |Cu +0,401 O 2 + 2H 2 O + 4 e  = 4OH  OH  |O 2 (Pt) +0,336 Cu 2+ + 2 e  = Cu Cu 2+ |Cu +0,153 Cu 2+ + e  = Cu + Cu 2+ ,Cu + |Pt +0,150 Sn 4+ + 2 e  = Sn 2+ Sn 4+ ,Sn 2+ |Pt

Termodinámica y Cinética de las Reacciones Electroquímicas Desde el punto de vista cuantitativo, existe una relación matemática entre el potencial de una celda y la concentración de reactivos y productos de una reacción redox cuando ésta se realiza en condiciones no estándar Es la Ecuación de Nernst Aunque más correctamente deberíamos hablar de actividades, en vez de concentraciones . Esta ecuación nos permite encontrar la fem que produce la celda en condiciones no estándar (ΔE) en función de ΔE° (potencial estándar de celda) y de las concentraciones de los reactivos y productos (expresados en Q). n son los moles de electrones transferidos y corresponde al número de electrones que se cancela al combinar las dos reacciones de media celda para obtener la reacción de celda. Esta ecuación también permite encontrar la concentración de reactivos y productos midiendo la fem de una celda.

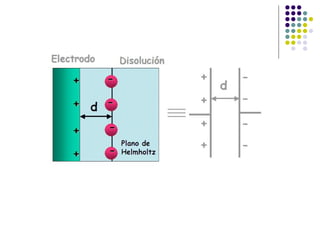
Si [productos] > [reactivos] ; Q > 1 y log Q > 0. El producto se resta de ΔE° y ΔE < ΔE°. Si [productos] < [reactivos] ; Q < 1 y log Q < 0 El producto se hace > 0 y ΔE > ΔE°. Potencial de celda y constante de equilibrio Si ΔG = 0 , el sistema está en equilibrio. como una fem = 0 significa que no se está produciendo una reacción neta en la celda voltaica, la reacción de la celda ha alcanzado el equilibrio. Cuando ΔE = 0, Q = K

Consideremos una reacción de transferencia electrónica de carga simple Ox + ne -  Red. Será útil suponer una celda con un electrodo de metal inerte y un electrodo de referencia sumergido y una disolución desoxigenada de baja concentración de Ox y Red, C Ox y C Red , respectivamente y una alta concentración de electrolito inerte. La única transferencia electrónica que puede tener lugar en la superficie del electrodo es la anteriormente citada. Potencial de equilibrio En la citada celda, cuando no hay un paso de corriente neta las concentraciones no pueden cambiar y el electrodo de trabajo debe tomar el potencial de equilibrio para la disolución, E e  Podrá ser medio mediante un voltímetro o calculado a partir de la ecuación de Nernst. Como en cualquier situación de equilibrio químico se establecerá una situación dinámica en la superficie del electrodo y tanto la reacción de reducción como de oxidación transcurren a la misma velocidad, por tanto, en términos de densidad de corriente, j (j = I/A) j a y j c son iguales y de signo contrario  estas densidades de corriente parciales pasan a ser un importante parámetro cinético que se denomina densidad de corriente de intercambio, j 0 Es una medida de la cantidad de actividad de transferencia electrónica en el potencial de equilibrio. También depende la concentración de los reactivos ( sea cual sea la constante de velocidad, probablemente, la reducción y la oxidación será de primero orden)

v c = k c C Ox v a = k a C Red En el equilibro v c = v a  k c C Ox = k a C Red Si C Ox = C Red  E= E 0 (potencial formal)  k c = k a = k 0 Constante de velocidad estándar. Consideremos ahora que al electrodo se le aplica un potencial E diferente al valor de equilibrio, el equilibrio se desplazará para alcanzar una nueva situación de equilibrio donde las concentraciones de Ox y Red en la disolución sean las que exija la ec. de Nernst. Si E > Ee la relación C Ox /C Red debe aumentar y una corriente anódica neta fluirá del electrolito hacia el electrodo para convertir Red en Ox Si E < Ee la relación C Ox /C Red debe disminuir y una corriente catódica neta fluirá desde el electrodo hacia la disolución para convertir Ox en Red Como la constante de velocidad está relacionada con la energía de activación según :

Y la velocidad del proceso electródico podemos convertirla en densidad de corriente, multiplicando por la carga Esta ecuación describe la densidad de corriente como una función del potencial del electrodo medido frente a un electrodo de referencia. Es más habitual escribirla de otra forma, obtenida mediante la introducción del sobrepotencial,  , que se define como  = E - E e o sea, la desviación del potencial respecto al potencial de equilibrio para el par Ox/Red

El uso del sobrepotencial tiene la ventaja de trasladar el potencial experimental desde una escala, que depende de la arbitraria elección del electrodo de referencia, a otra escala que solo depende de la química del par redox bajo estudio. La ecuación puede ser simplificada teniendo en cuenta que la densidad de corriente parcial anódica y catódica en el potencial de equilibrio es igual y conocida como densidad de corriente de intercambio: Y aplicando la definición de sobrepotencial, queda : Ecuación de Butler-Volmer

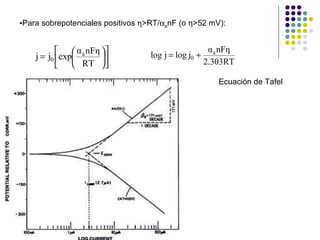
La densidad de corriente observada a cada valor de sobrepotencial,  , j depende de: La densidad de corriente de intercambio, j 0 . Los coeficientes de transferencia,  a y  c . La temperatura. Cuando la densidad de corriente puede medirse a sobrepotenciales positivos y negativos, conviene modificar la ecuación de Butler-Volmer para analizar mejor los datos. Así, si dividimos por exp(  a nF  /RT) la ecuación de Butler-Volmer y aceptando que  c = 1-  a , se obtiene : Así midiendo j y  , se puede representar log [ ] frente a  y debe ser una línea recta de donde se pueden determinar parámetros cinéticos de la ordenada en el origen, j 0 , y de la pendiente,  a .

Para sobrepotenciales positivos  >RT/  a nF (o  >52 mV): Ecuación de Tafel

b) Para sobrepotenciales negativos  < -RT/  c nF (o  < -52 mV): Es decir, a sobrepotenciales positivos y negativos, existe una relación lineal entre log j y  . Extrapolando ambas líneas hasta h, puede obtenerse j 0 y los coeficientes de la transferencia se obtienen de la pendiente.

La doble capa En todos los procesos de electrodo, es decir en aquellos donde el proceso electroquímico se establece en la región que incluye la interfaz electrodo-solución se genera una distribución de cargas (aún cuando no se aplique un potencial al electrodo) conocida como doble capa eléctrica. Es de gran importancia el estudio de los procesos que ocurren a nivel de esta zona puesto que de esta manera se tendrá una mejor comprensión del comportamiento macroscópico del sistema. Teoría De La Doble Capa El estudio de la distribución de carga en la vecindad de la interfase ha sido motivo de interés de científicos desde mediados del siglo XIX, es así que se destacan los aportes realizados por: - Helmholtz (1879) - Gouy (1910) - Chapman (1913) - Stern (1924) - Grahame (1947) Estos estudios han tenido como propósito elaborar un modelo de doble capa que permita interpretar como varía el potencial eléctrico desde la superficie metálica hasta el seno de la solución.

De acuerdo a esta teoría la interfaz se considera similar a un condensador eléctrico, es decir dos placas paralelas cargadas y separadas una distancia d. De acuerdo a esta analogía se puede definir la capacidad por unidad de área de la doble capa eléctrica como: donde C es la constante dieléctrica del medio. De acuerdo con esa ecuación la capacidad de la doble capa debería ser independiente del potencial. Sin embargo experimentalmente puede verificarse que no solo existe esa dependencia sino que también varía de acuerdo a la concentración iónica de la solución y a la naturaleza de sus componentes. Todo lo anterior indica que el modelo presenta inconsistencias con la realidad por lo que deben ser tenido en cuenta estos factores. MODELO DE HELMHOLTZ PARA LA DOBLE CAPA ELÉCTRICA Es el modelo mas simple de la doble capa eléctrica. El exceso de iones en el lado de la solución de la doble capa, se encuentra ubicado en un plano ("plano de Helmholtz") muy cercano a la superficie del electrodo.

MODELO DE GOUY-CHAPMAN De acuerdo con este modelo, el exceso de iones no están distribuidos uniformemente en la vecindad del electrodo, su concentración es mayor en la superficie del electrodo y decrece no linealmente hasta alcanzar la concentración del seno de la solución. Los iones en exceso en la capa difusa están de una parte atraídos por la capa interfacial, y por otra parte tienden a dispersarse bajo el efecto de la difusión y de la presión osmótica que tiende a igualar las concentraciones. El resultado de estos dos efectos es una distribución de Boltzman semejante a la distribución másica de moléculas en el campo gravitacional

1) El espesor de la capa difusa aumenta cuando aumenta la constante dieléctrica (o la permitividad) del medio, produciéndose un mayor efecto de pantalla. 2) El espesor de la capa difusa disminuye cuando aumenta la concentración del electrólito. 3) Cuando mayor la carga de los iones (Zi), mayor la reducción del espesor de la capa difusa. 4) Finalmente el espesor de la capa difusa aumenta con la temperatura. Esto se debe al aumento de las fuerzas que promueven la difusión. Sin embargo este efecto es relativamente menor debido al estrecho rango de variación de T (273 - 373 °K para agua líquida). Ya que los efectos electrocinéticos dependen de la doble capa, las tendencias anteriores tienen importantes aplicaciones prácticas El modelo de GOUY-CHAPMAN supone un potencial bajo y una concentración iónica baja. Por otra parte, un ion de la capa difusa no puede acercarse a la superficie a una distancia inferior a su radio (como ion solvatado), lo que hace que la distribución de Boltzman no sea aplicable muy cerca de la interfase. Finalmente el tratamiento de GOUY-CHAPMAN supone que la constante dieléctrica del medio es la del solvente; en realidad dicho parámetro varía con la concentración de electrólitos.

MODELO DE GOUY-CHAPMAN-STERN A diferencia del modelo de Gouy-Chapman donde se predice que idealmente puede conseguirse gran concentración superficial, dado que se asume que los iones son infinitamente pequeños y pueden acercarse libremente a la superficie del electrodo; este modificación, llamada "modificación de Stern" es en esencia una combinación de los modelos de Helmholtz y Gouy-Chapman. En él, se asume un plano de aproximación mas próxima, donde reside una porción de los iones en exceso y están unidos a una capa difusional como la predice el modelo de Gouy-Chapman . El primer caso corresponde a una interfase sólida cargada positivamente, con una capa adsorbida de Stern cargada negativamente, pero de carga insuficiente para asegurar la electroneutralidad. En consecuencia la capa difusa posee la carga negativa complementaria. En el segundo caso la carga negativa de la capa de Stern excede la carga positiva de la interfase sólida. En tal caso la capa difusa posee una capa neta positiva.

El tercer (el más común) y el cuarto caso ilustran los fenómenos correspondientes con una interfase sólida cargada negativamente. El exceso o defecto de carga de la capa de Stern respecto a la interfase sólida depende de las fuerzas que determinan la adsorción de los iones y del estado de carga superficial respecto al punto de carga cero. Una de las aplicaciones de la doble capa eléctrica es la interpretación de las fuerzas de repulsión que aparecen entre gotas o partículas cuando estas se acercan

Conviene recordar el orden de magnitud de las distancias y fenómenos involucrados. Capa adsorbida de Stern (x 1 ) 1 - 5 Å " Espesor " de la capa difusa (  ). 50 - 200 Å Límite de resolución óptica visible. 5000 Å

La doble capa influye en las reacciones electroquímicas pues influye debido a que : Sus propiedades son muy diferentes a las del resto de la disolución, pudiéndose alcanzar valores del campo eléctrico del orden de 10 7 V/cmc campo ante el que la mayor parte de las moléculas experimenta alguna transformación. La reacción depende de la diferencia de potencial en la interfase electrodo- disolución, y dicha d.d.p. depende de la composición y estructura de la doble capa. Los “ladrillos” de la doble capa son los iones del electrolito soporte Sin embargo, la doble capa apenas influye en la transferencia de materia disolución-electrodo-disolución

Para que se produzca la transferencia electrónica es preciso que los reactivos estén en las proximidades del electrodo, dentro de la zona compacta de la doble capa. Para ello es indispensable que se produzca el transporte de materia de los reactivos desde la disolución a la interfase electrodo-disolución, así como de los productos desde dicha interfase a la disolución . En otras palabras, la velocidad de una reacción electroquímica no puede ser superior a la velocidad con la que el reactivo alcanza la superficie electródica. La transferencia electrónica depende, por tanto, de la transferencia de materia. En electroquímica se consideran los siguientes mecanismos de transporte de materia: Difusión : surge como consecuencia del gradiente de concentración que existe entre la interfase y el resto de la disolución, esto es, la difusión es un proceso físico que causa el transporte de especies de una región de la disolución concentrada a una región que es más diluida, hasta que las concentraciones sean iguales. La difusión se describe mediante las leyes de FICK 1ª Ley de Fick: describe la velocidad de difusión (flujo) como función del gradiente de concentración (fuerza impulsora de la difusión )

J= flujo de la especie (mol·m -2 ·s -1 ) gradiente de concentración en la dirección x perpendicular a la superficie plana. D= coeficiente de difusión (en agua 10 -5 -10 -6 cm 2 ·s -1 ) 2ª Ley de FICK: describe el cambio con el tiempo de la concentración en el centro de un elemento de volumen limitado por dos planos paralelos a la superficie. La concentración cambia debido a la difusión de las especies que entran al elemento a través de un plano y que sale por el otro. Integrando esta ecuación y resolviendo para condiciones límites x = 0, llegamos a la ecuación de COTTRELL

b) Migración : se debe al movimiento de las especies cargadas por la presencia de un campo eléctrico. Normalmente se añade una alta concentración de electrólito inerte a la disolución que contiene las especies electroactivas y con eso se asegura que la migración no contribuye al transporte de la especies electroactivas. El reactivo y/o el producto será especies electroactivas serán especies cargadas pero si ellos están rodeadas por un exceso de iones serán éstos quienes migren. En las proximidades del electrodo, la especie electro-activa es transportada por difusión y por migración, por lo que la corriente total, i , será la suma de las componentes difusiva y migracional: i = id ± im donde im y id pueden tener la misma dirección u opuesta, dependiendo de la dirección del campo eléctrico y de la carga de las especies electro-activas ,

Se puede demostrar que : donde i es la intensidad de la corriente total, n el número de electrones que interviene en la reacción de electrólisis del ión A , z A , su carga y t A su número de transporte. Por su parte , t A es : Δ A z A C A  Δ i z i C i En electro-análisis, la forma de transporte por migración se considera indeseable, por lo que para minimizar su efecto, lo que se hace es disminuir el número de transporte, t A , operando con una relación C A /C i muy pequeña. Esto se consigue añadiendo un exceso (unas 100 veces) de electrolito soporte , constituido por especies no electro-activas (normalmente, nitratos, sulfatos o percloratos alcalinos)

c) La convección consiste en el desplazamiento de sustancias bajo la influencia de agitación o cualquier otra forma de transporte hidrodinámico, como diferencias de densidad, de temperatura, choques, vibraciones, etc. Todos estos fenómenos se incluyen bajo la denominación de convección. Estas tres formas de transporte de materia a un electrodo están recogidas en la ecuación de Nernst–Planck, que para una transferencia de masa unidireccional a lo largo del eje x, es: La resolución rigurosa de esa ecuación no es, generalmente, fácil, y los sistemas electroquímicos suelen diseñarse de manera que algunos términos sean despreciables

En resumen, la velocidad de una reacción electroquímica dependerá del sobrepotencial aplicado. A bajos sobrepotenciales, la etapa determinante es la transferencia electrónica. La densidad de corriente no depende del mecanismo de transporte de materia Al aumentar el sobrepotencial, ambas velocidades son comparables, el control de la reacción es mixto. La densidad de corriente depende parcialmente de los mecanismos de transporte de materia. A mayores sobrepotenciales, la velocidad de transferencia de carga es tan rápida que la etapa que controla la velocidad es la transferencia de materia. La concentración de reactivo en la superficie del electrodo es cero, el reactivo se consume tan rápidamente como llega al electrodo. A esta densidad de corriente se la denomina intensidad de corriente limitante

Adsorción La adsorción es la interacción de especies de la disolución con la superficie del electrodo. Las especies adsorbidas pueden ser reactivos, intermedios o el producto o incluso una especie no implicada en el proceso de transferencia electrónica pero capaz de cambiar la velocidad o mecanismo de la reacción electródica. Pueden adsorberse especies orgánicas, inorgánicas, iones y moléculas neutras. Todos estos procesos pueden ser reversibles o irreversibles Los mecanismos de adsorción son los siguientes: Adsorción física, debida a fuerzas electrostáticas y a interacciones dipolo-dipolo. Adsorción química, debida a fuerzas similares a las responsables de enlaces químicos. Electroadsorción, consecuencia directa de la aplicación del campo eléctrico La extensión de la adsorción, a menudo expresada como una fracción de la superficie electródica cubierta por el adsorbato,  , se puede enfocar en términos de dos competiciones: 1.- entre la superficie y la disolución por los adsorbatos potenciales. 2.- entre todas las especies en la disolución (especies electroactivas, moléculas de disolvente, iones electrolito inerte, impurezas y aditivos deliberadamente introducidos dentro de la disolución) por los sitios de la superficie electródica.

La tendencia de una especie a adsorberse se expresa como una energía libre de adsorción,  G ads . El grado de adsorción de cada sustancia depende de numerosos factores: potencial aplicado, material electródico (afinidad por la superficie), pH, temperatura, disolvente, electrolitos, impurezas y la extensión en las que las especies están solvatados o estabilizados por otras interacciones en la disolución. Normalmente, las moléculas neutras orgánicas están fuertemente adsorbidas en los potenciales donde la superficie no tiene carga (potencial de carga cero) ya que la competición por la adsorción de iones y dipolos fuertes está en el mínimo. La adsorción es de interés ya que los adsorbatos sobre superficie del electrodo pueden provocar cambios muy sustanciales en la velocidad de las reacciones, así como, cambiar el mecanismo e incluso los productos de las reacciones electródicas. Estos efectos son el centro de muchos experimentos en el laboratorio y de muchas aplicaciones de la electroquímica en tecnología: Electrocatálisis: el catalizador es comúnmente una especie adsorbida. Inhibición de la transferencia electrónica: corrosión. Nueva química: algunas reacciones sintéticas parecen ser totalmente específicas a uno o varios materiales electródicas. Muchos procesos de adsorción son completamente reversibles y la extensión de la adsorción se discute en términos de isotermas de adsorción: cuantifican la relación, a temperatura constante, entre fracción de la superficie cubierta por el adsorbato,  , su  G ads , y la concentración de adsorbato en la disolución. Hay muchas isotermas que difieren en la extensión y el método de tener en cuenta las interacciones laterales entre las especies adyacentes adsorbidas :

Isoterma de Langmuir : supone que no existen interacciones laterales y, por tanto,  G ads es independiente del recubrimiento. Isoterma de Frumkin : supone que es más difícil adsorber según aumenta el recubrimiento, (cuantitativamente  G ads aumenta linealmente con el recubrimiento). g= parámetro que da idea de la energía de interacción entre especies adsorbidas, variando con el recubrimiento

Cuando el adsorbato es: Electroinactivo  el recubrimiento se deduce por medio de la capacitancia de la interfase como función de la concentración del adsorbato. Electroactivo  el proceso de adsorción se estudia registrando de curvas j frente a potencial. Cuando el proceso de adsorción es irreversible, no puede usarse isotermas para describirlo

Reacciones de Transferencia Electrónica Múltiple Muchas reacciones electródicas implican la transferencia de más de un electrón sin un estado de oxidación intermedio claramente identificable, en tales casos, es importante ver el mecanismo para decidir si los electrones se transfieren simultáneamente o en varios saltos electrónicos simples. Por ejemplo, el par Cu(II)/Cu en disoluciones acuosas de sulfato en medio ácido. Si la transferencia es simultánea, podríamos aplicar la ecuación de Butler-Volmer, con n = 2 y representaríamos los datos de corriente vs potencial y las gráficas para la oxidación y reducción tendrían unas pendientes de + 1/60 mv y – 1/60 mv, respectivamente. Si la transferencia es por pasos, la gráfica tomará una forma diferente que dependerá de cual sea el paso determinante de la velocidad. Experimentalmente, se determina que las pendientes son -1/120 mv y +1/40 mv, por lo que se puede concluir que los electrones son transferidos en etapas discretas de un electrón

Electroquímica industrial

Más contenido relacionado

La actualidad más candente

Similar a Electroquímica industrial

Último

Electroquímica industrial