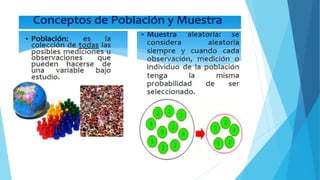
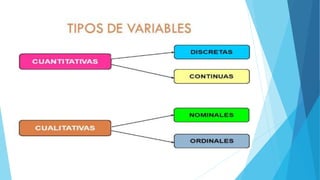
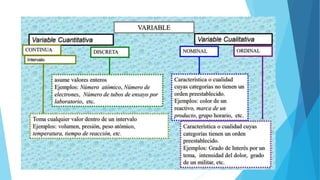
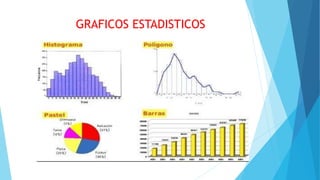
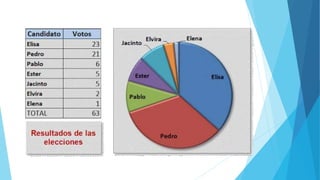
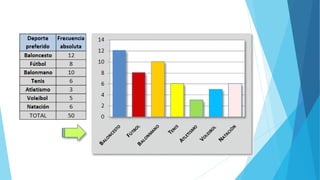
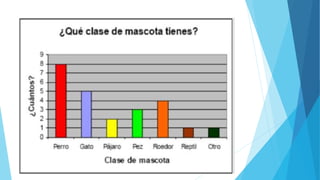
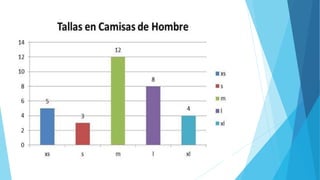
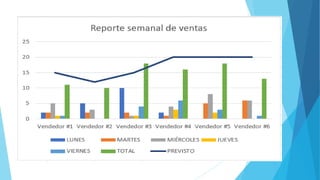
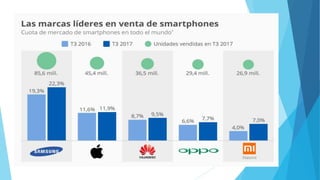
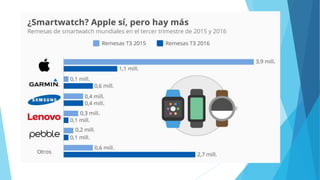
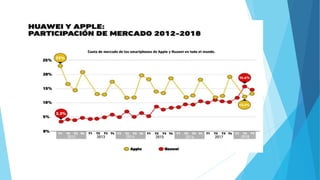
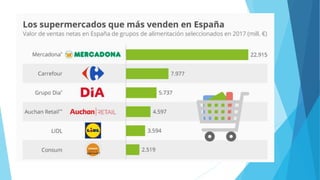
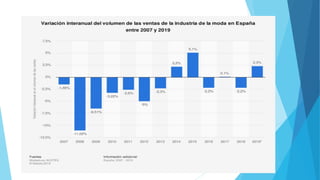
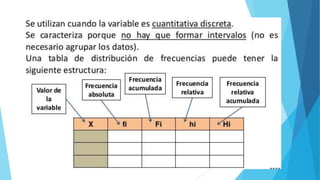
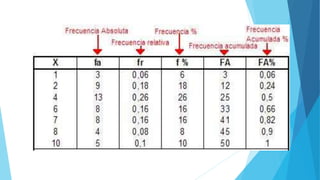
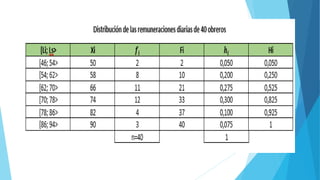
Este documento presenta diferentes tipos de variables estadísticas, incluyendo variables cuantitativas discretas y continuas, y variables cualitativas nominales y ordinales. También explica cómo calcular frecuencias absolutas, relativas y porcentuales, y cómo construir cuadros estadísticos para variables cuantitativas discretas y continuas.