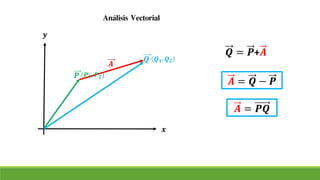
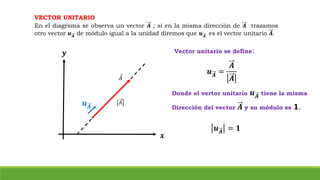
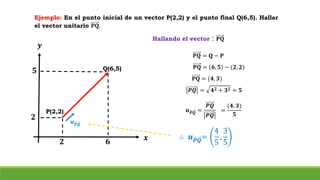
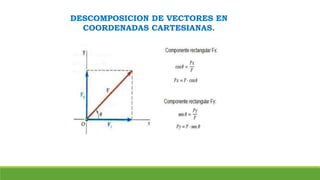
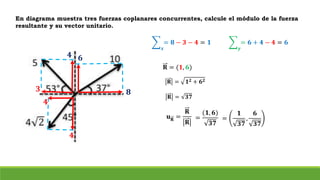
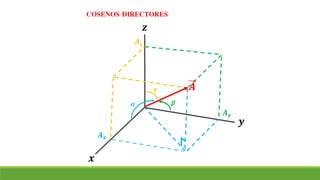
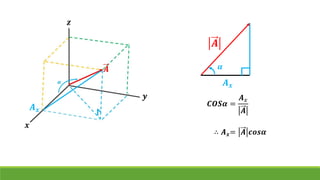
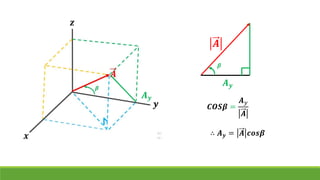
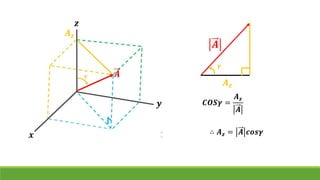
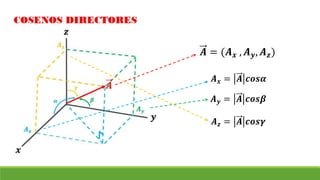
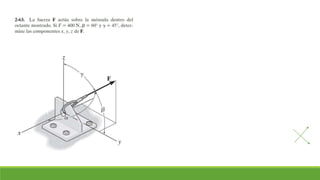
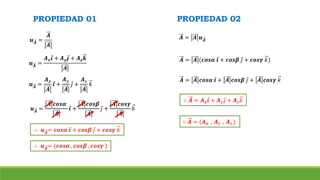
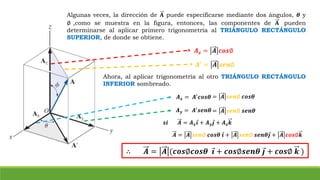
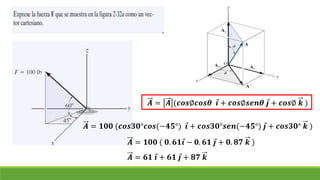
El documento resume conceptos clave sobre vectores unitarios, descomposición de vectores y cosenos directores. Explica cómo calcular un vector unitario dividiendo un vector por su magnitud. También explica cómo descomponer un vector en sus componentes cartesianas y cómo representar la dirección de un vector mediante cosenos directores y ángulos.
Aplicaciones de espacios y subespacios vectoriales en la carrera de Electróni...MATEOESTEBANCALDERON
Los espacios y sub-espacios vectoriales están aplicados en muchos campos de la vida cotidiana, en ingeniería, es muy útil para todo sin embargo en este trabajo analizaremos su aplicación a un área específica de la ingeniería electrónica y automatización.
Aplicaciones de espacios y subespacios vectoriales en la carrera de Electróni...MATEOESTEBANCALDERON
Los espacios y sub-espacios vectoriales están aplicados en muchos campos de la vida cotidiana, en ingeniería, es muy útil para todo sin embargo en este trabajo analizaremos su aplicación a un área específica de la ingeniería electrónica y automatización.
Es un formulario sobre los teoremas y leyes de los vectores en el plano (2D) y en el espacio (3D).
El hecho que tiene graficas ayuda mejor a su comprencion y solucion de problemas físicos.
Instrucciones del procedimiento para la oferta y la gestión conjunta del proceso de admisión a los centros públicos de primer ciclo de educación infantil de Pamplona para el curso 2024-2025.
3. VECTOR UNITARIO
En el diagrama se observa un vector 𝑨 ; si en la misma dirección de 𝑨 trazamos
otro vector 𝒖 𝑨 de módulo igual a la unidad diremos que 𝒖 𝑨 es el vector unitario 𝑨.
𝐴
𝒖 𝑨
𝐴
𝒖 𝑨 =
𝑨
𝑨
Vector unitario se define:
𝒙
𝒚
Donde el vertor unitario 𝒖 𝑨 tiene la misma
Dirección del vector 𝑨 y su módulo es 1.
𝒖 𝑨 = 𝟏
4. Ejemplo: En el punto inicial de un vector P(2,2) y el punto final Q(6,5). Hallar
el vector unitario 𝐏𝐐.
𝒖 𝑷𝑸
𝒖 𝑷𝑸 =
𝑷𝑸
𝑷𝑸
𝒙
𝒚
𝟐
𝟐
𝟓
𝟔
P(2,2)
Q(6,5)
Hallando el vector : 𝐏𝐐
𝐏𝐐 = 𝐐 − 𝐏
𝐏𝐐 = 𝟔, 𝟓 − (𝟐, 𝟐)
𝐏𝐐 = (𝟒, 𝟑)
𝑷𝑸 = 𝟒 𝟐 + 𝟑 𝟐 = 𝟓
=
(𝟒, 𝟑)
𝟓
∴ 𝒖 𝑷𝑸=
4
5
,
3
5
