Método de la doble integración para calcular deformaciones en vigas

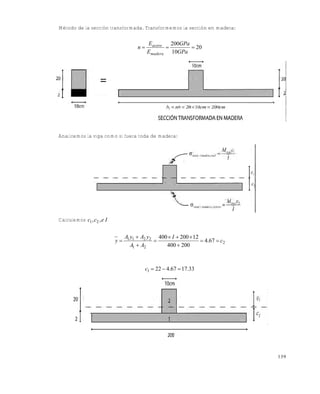
139
Método de la sección transformada. Transformemos la sección en madera:
20
10
200

GPa
GPa
E
E
n
madera
acero
Analicemos la viga como si fuera toda de madera:
Calculemos Iecc ,, 21
2
21
2211
67.4
200400
12200400
c
I
AA
yAyA
y 






33.1767.4221 c
Este documento se cre€ con la versi€n gratuita de EVALUACI•N de eXpert PDF. Esta marca de agua se eliminar‚ al
comprar la licencia de la versi€n completa de eXpert PDF. Visite www.avanquest.es para obtener m‚s informaci€n

140
  422
67.2292267.260027200 cmAdII D 
4
33
27200
3
2010
3
2200
cmID 




Finalmente, calculamos los esfuerzos en la madera y en el acero:
KPa.
m
cm
cm
N
.
cm.
cm.cmN
I
cMmax
real,madera)max( 62721
10
16272
6722922
33171003600
2
24
24
1


 
KPa.
m
cm
cm
N
.
cm.
cm.cmN
I
cMmax
ficticio,madera)max( 4733
10
3473
6722922
6741003600
2
24
24
2


 
Como en la realidad en la parte inferior de la viga no hay madera sino una platina de acero,
debemos “devolvernos” por as‚ decirlo y multiplicar este esfuerzo ficticio por n para obtener el
esfuerzo real en el acero:
KPaKPan ficticiomaderarealacero 149547.74720,)max(,)max(   
En conclusiƒn hemos encontrado los siguientes esfuerzos m„ximos en la viga:

141
Variación de esfuerzos a través de la sección:
La viga entonces, absorberá los esfuerzos de la siguiente forma:
Como se ve, la platina de acero soporta la mayor parte de los esfuerzos de tensión.
La viga también puede analizarse transformando toda la sección en acero. Veámoslo a
continuación.
Resolución del problema transformando la viga en acero
Vamos a transformar toda la viga en acero. Por lo tanto:
05.0
200
10

GPa
GPa
E
E
n
acero
madera

142
Sección transformada en acero
Analicemos la sección transformada:
2
21
2211
67.4
1020
1210120
c
AA
yAyA
y 






33.1767.4221 c
Cálculo del momento de inercia:
  13.114667.2301360 22
 AdII D
1360
3
205.0
3
210 33




DI

143
Cálculo de los esfuerzos:
Esfuerzo máximo en la madera:
KPan ficticioaceroCrealmaderaC 6.27745549205.0,)max(,)max(  
En resumen:
Obviamente, los valores son
iguales a los que obtuvimos
transformando la sección en
madera
KPaPaficticioaceroC 554921020.5549
13.1146
33.171003670 4
,)max( 


KPaParealaceroT 7.149531037.1493
13.1146
67.41003670 4
,)max( 


KParealmaderaC 6.2774,)max( 
KParealaceroT 7.14953,)max( 

144
PROBLEMAS PROPUESTOS
Calcular los esfuerzos normales y cortantes máximos en las siguientes vigas

145
C A P Í T U L O 4
D E F O R M A C I O N E S E N V I G A S
NÓTENSE LAS DEFORMACIONES Y FISURAS EN LOS EXTREMOS DE LA VIGA
Tal como se ha dicho, un elemento estructural no sólo debe ser resistente a la rotura sino que
debe tener unas condiciones de rigidez adecuadas de tal manera que se cumplan algunas condiciones
mínimas, a saber:
 Que se garantice la funcionalidad de la estructura evitando grandes deformaciones que podrían
afectar su desempeño. (Por ejemplo el alineamiento y nivelación de equipos).
 Que no se afecte la estética de la estructura con la aparición de grietas, producto de grandes
deformaciones.

146
NÓTESE AGRIETAMIENTO DE LA VIGA EN LA SECCIÓN DE MOMENTO NEGATIVO,
POR FALTA DE REFUERZO
Adicionalmente como se ha visto, en el caso de vigas estáticamente indeterminadas es necesario
obtener ecuaciones adicionales basadas en las deformaciones que nos ayuden a levantar la
indeterminación y así poder resolverlas.
De otra parte, en los próximos cursos de ingeniería estructural se requerirán los conocimientos
relativos a los métodos de cálculo de deformaciones en vigas para poder afrontar elestudio de estructuras
estaticamente indeterminadas (por ejemplo en el método conocido como pendiente- deflexión o slope
deflection).
Por estos motivos se hace necesario calcular las deformaciones que se producen en las vigas
cuando están son sometidas a cargas.
Existen varios métodos para calcular las deformaciones en vigas:
 Métodos matemáticos: Método de la doble integración o de la Ecuación de la elástica.
 Métodos geométricos: Basados en la forma de la viga deformada. El mas conocido es el
método del Área de momentos o Teoremas de Mohr.
 Métodos derivados de los anteriores: Método de la viga conjugada conocido en algunos
textos como Método de los Pesos Elásticos.
 Métodos energéticos: Basados en la conservación de la energía desarrollada por las fuerzas
al deformar las vigas. (Teoremas de Maxwell, de Castigliano y otros).

147
Tipos de deformaciones

148

149
Funcionalidad afectada por deformaciones excesivas (se desnivelan los elementos soportados
por la viga).
Deformaciones excesivas pueden causar agrietamientos que afectan la estética de las estructuras.

150
Deformaciones con concavidades contrarias.
4.1 MÉTODO DE LA DOBLE INTEGRACIÓN
En la teoría de flexión se vió que:
EI
M


1
En matemáticas se tiene que:
  2
3
2
2
2
1
1



 

dx
dy
dx
yd


151
Por lo tanto:
  EI
M
dx
dy
dx
yd




 
2
3
2
2
2
1
pero 0





dx
dy
las pendientes en las vigas son muy peque€as
Con mayor raz•n: 0
2






dx
dy
En conclusi•n: "2
2
y
EI
M
dx
yd
 o lo que es lo mismo: MEIy "
EI: Rigidez a la flexi•n
y‘’ : segunda derivada de la ecuaci•n de la viga deformada o el‚stica
M: Ecuaci•n del momento flector en el tramo de viga considerado
Si integramos esta ecuaci•n obtenemos la ecuaci•n de la pendiente y’:
  1CMdxyEI
Si integramos otra vez (doble integraci•n) obtenemos la ECUACI„N DE LA EL…STICA:
  21 CxCMdxEIy ECUACI„N DE LA EL…STICA
Con estas ecuaci•n podemos calcular la pendiente y’ o la deformacion y en cualquier punto de la viga.
Las constantes C1 y C2 se calculan estableciendo las condiciones iniciales o de borde que dependen
de los apoyos y las caracter†sticas de la viga y de las cargas como se ver‚ en los ejemplos.
MEIy "

152
CONDICIONES INICIALES EN DIFERENTES TIPOS DE VIGAS

153
PROBLEMA
Calcular la deformación en el extremo libre B de la viga en voladizo:
Tal como se vió en el método de doble integración:
MEIy "
Para poder integrar necesitamos la ecuación del momento flector M. Para encontrarla hacemos
un corte a una distancia x del empotramiento A.
  0M 0 PxPLM
Ecuación del momento:
PLPxM 
Por lo tanto:
PLPxEIy "
Integrando una vez:
1
2
2
CPLx
Px
yEI 
Integrando otra vez (doble integración):
21
23
26
CxC
PLxPx
EIy 

154
Para calcular C1 y C2 debemos establecer las condiciones iniciales. Para esto, observamos el
problema f€sico, la viga empotrada en A. En el empotramiento (x=0) se est•n impidiendo tanto
la deformaci‚n (y=0) como el giro (y’=0). Recordemos que un empotramiento por definici‚n es
un apoyo que impide el giro.
Entonces:
Condiciones iniciales:
00
00


yx
yx
00  yx 21
23
26
CxC
PLxPx
EIy  por tanto: 02 C
00  yx 1
2
2
CPLx
Px
yEI  por tanto: 01 C
Al ser las dos constantes iguales a cero, las ecuaciones quedan:
Ecuaci‚n de la el•stica:









26
1
26
2323
PLxPx
EI
y
PLxPx
EIy
Ecuaci‚n de la pendiente:








 PLx
Px
EI
yPLx
Px
yEI
2
1
2
22
C•lculo de la deformaci‚n en el extremo B:
 LB y
0 0 0
0 0 0 0

155
EI
PLPLPL
EI
B
326
1 333










EI
PL
B
3
3

Análisis de deformación
Vemos que mientras mayores sean P y L mayor será la deformación y que mientras mayor sea EI,
será menor.
EI: Rigidez a la flexión. Para un material dado (E), la deformación depende del momento de la
inercia.
Influencia del momento de inercia en la deformación
Influencia de la longitud de la viga L en la deformación
 LB y









26
1 23
PLxPx
EI
y
EI
PL
B
3
3


156
Si duplicamos la longitud de la viga tendremos:
| Al duplicar la longitud, la
deformación se hace 8 veces
más grande
Cálculo de la pendiente de la viga en B:
Ecuación pendiente:








 PLx
Px
EI
y
6
1 2
 LB y
|
EI
PL
PL
PL
EI
B
22
1 2
2
2










EI
PL
B
3
3

 
EI
PL
EI
LP
B
3
8
3
2 33


157
PROBLEMA
Calcular la deformación máxima en la viga, la pendiente en los apoyos A y B y la deformación
en el centro de la luz
3000500350  BBA RRM
  2003005000 Ay RF
En este caso la ecuación de momentos no es única para toda la viga: tiene una expresión distinta
en cada uno de los 2 tramos. Veamos:
30  x
xM 200
53  x
Encontremos la ecuación de la elástica para cada tramo:
 3500200  xxM
 
 
 
21
33
21
3
1
22
1
2
6
3500
6
200
6
200
2
3500
2
200
2
200
3500200"200"
5330
DxD
xx
EIyCxC
x
EIy
D
xx
yEIC
x
yEI
xxEIyxEIy
xx








Tenemos 4 constantes.
Necesitamos por tanto
4 condiciones iniciales

158
02 C
05
6
2500
6
5200
0 21
33




 CD
211 55 DDC 
11 DC 
De estas cuatro ecuaciones obtenemos:
70000 1122  DCDC
CBAC
CBAC
yyx
yyx


3
3
C es un punto común de los
tramos AC y CB. Por tanto en
dicho punto las ordenadas y las
pendientes de los 2 tramos son
iguales
 
 
 
1
22
1
3
21
33
1
3
21
33
1
3
2
3500
2
200
2
200
6
3500
6
200
6
200
6
3500
6
200
6
200
00
2
D
xx
yEIC
x
EIyyy3x
DxD
xx
EIyCxC
x
EIyyy3x
DxD
xx
EIy0y5x
CxC
x
EIyyx
CBAC
CBAC
2











159
Deformaci‚n m•xima: Por observaci‚n vemos que ocurre en el tramo AC de la viga. Adem• es
en dicho punto la tangente a la el•stica horizontal, es decir y’=0.
La ecuaci‚n de la pendiente para el tramo AC es:
1
2
2
200
C
x
yEI 
Por tanto:
700
2
200
2
200
0
2
1
2

x
C
x
65.2x En este punto ocurre la deformaci‚n m•xima
 
EIEI
y 2.65
68.1234
65.2700
6
65.22001 3
max 











Pendientes en los apoyos A y B:
 
EIEI
C
x
EI
y 0A
700
700
2
02001
2
2001 2
1
2





















 
   
EIEI
D
xx
EI
y 5B
800
700
2
35500
2
52001
2
3500
2
2001 22
1
22

























Deformaci‚n en el centro de la viga:
 
EIEI
y 2.5centro
17.1229
5.2700
6
5.22001 3












0yeny max

160
En resumen:
PROBLEMA
Calcular la deformación máxima en la viga que tiene rigidez a la flexión EI:




1220338046000
338008400036000
Ay
BBA
RF
R10RM

161
Ecuaciones del momento flector:
30  x xM 1220
6x3   3-x-xM 6001220
106  x
    
2
6
6100036001220


x
xxxM
   
2
6
100036001220
2


x
xxM

162
Pero: MyEI 
30  x x 63 
xEIy 1220"  36001220 -x-xEIy" 
C
x
yEI 1
2
2
1220

 
1
2
2
3600
2
1220
D
xx
EIy
2



21
3
6
1220
CxC
x
EIy 
 
21
33
6
3600
6
1220
DxD
xx
EIy 


C
x
yEI 1
2
2
1220

  D
xx
yEI 1
22
2
3600
2
1220



21
3
6
1220
CxC
x
EIy 
 
21
33
6
3600
6
1220
DxD
xx
EIy 


106  x
   
2
6
10006001220
2


x
3-x-xEIy"
   
1
322
6
6
1000
2
3600
2
1220
E
x-xx
yEI 


   
21
433
24
6
1000
6
3600
6
1220
ExE
x-xx
EIy 


   
1
322
6
6
1000
2
3600
2
1220
E
xxx
yEI 




   
21
433
24
6
1000
6
3600
6
1220
ExE
xxx
EIy 





163
CxC
x
EIy0y0x 21
3
6
1220

02C
  DxD
xx
EIyCxC
x
EIyyy3x CDAC 21
33
21
3
6
3600
6
1220
6
1220



211 33 DDC 
  D
xx
yEIC
x
yEIyyx CDAC 1
22
1
2
2
3600
2
1220
2
1220
3 


1DC1 
     
21
433
21
33
24
6
1000
6
3600
6
1220
6
3600
6
1220
6 ExE
xxx
EIyDxD
xx
EIyyyx DBCD 






2121 66 EEDD 
     
1
32222
6
6
1000
2
3600
2
1220
2
3600
2
1220
6 E
xx
-
x
yEID
xx
yEIyyx 1DBCD 






1ED1 
       
21
433
21
433
10
24
610
1000
6
310600
6
101220
24
6
1000
6
3600
6
1220
10 EE0ExE
xxx
EIy0yx 










2110671583660 EE. 

164
En últimas, tenemos: Resolviendo el sistema, las constantes
tienen los siguientes valores:
02C 02C
211 33 DDC  02 D
11 DC  67.158361 C
2121 66 EEDD  022  DE
11 ED  67.158361 D
211067.1583660 EE  67.158361 E
Cálculo de la deformación máxima
Por observación, vemos que estará ubicada en el tramo central de la viga. La condición es que
allí la pendiente debe valer cero (tangente horizontal). Por tanto:
La ecuación de la pendiente para el tramo CD es:
 
1
22
2
3600
2
1220
D
xx
yEI 


Por tanto:
  67.15836
2
3600
2
1220
0
22



xx
Resolviendo la ecuación de segundo grado:
73.11
92.5
2
1


x
x
La raíz 73.112 x solo tiene significado matemático. Para nosotros el valor que tiene significado
físico para la viga que estamos analizando es el de 92.51 x . Chequeamos además que está
comprendido en el tramo 63  x .

165
Por lo tanto:
 ymaxima 92.5 en la ecuación de y válida en dicho punto:
 
21
33
6
3600
6
1220
DxD
xx
EIy 


 
 
EIEI
1
ymaxima
28.54056
92.567.15836
6
392.5600
6
92.51220 33
92.5 













925
28.54056
.xen
EI
maxima 
4.1.1 FUNCIONES DE SINGULARIDAD
Observemos las ecuaciones del momento flector para la viga del problema anterior:
 
   
2
6
100036001220106
30
2




x
xxMx
3-x600-1220xM6x3
1220xMx

166
Como se ve, cada ecuaci•n es igual a la anterior mas un t‡rmino, de tal manera que la ˆltima las
“contiene” a todas por as† decirlo, lo cual la convierte en la ecuaci•n representativa de la viga.
    106
2
6
100036001220
2


 x
x
xxM
     63
2
6
6100036001220
2


 x
x
xxxM
     30
2
6
6100036001220
2


 x
x
xxxM
Este hecho hace que podamos utilizar la ˆltima ecuaci•n como representativa de la viga con una
condici•n: que para cada tramo solo se incluyan los t‡rminos necesarios.
Esto se logra utilizando FUNCIONES DE SINGULARIDAD, que tienen una expresi•n distinta
para cada tramo incluyendo los t‡rminos afectados por par‡ntesis solo cuando se necesiten.
Matem‚ticamente esto se expresa escribiendo la ecuaci•n con par‡ntesis angulares los cuales s•lo se
incluir‚n en la ecuaci•n cuando su valor sea positivo segˆn la siguiente convenci•n:
ECUACI„N REPRESENTATIVA DE LA VIGA:
2
6
100036001220
2


x
xxM
Condici•n para los par‡ntesis:
 
axsiax
axsiaxax


0
Resolvamos el problema anterior utilizando funciones de singularidad:
Si le quitamos un
término, se convierte en
la segunda:
Si le quitamos otro
término, se convierte en
la primera:

167
 
   
2
6
100036001220106
36001220
122030
2




x
xxMx
x-x-M6x3
xMx
ECUACIÓN REPRESENTATIVA DE LA VIGA:
2
6
100036001220
2


x
xxM
Por lo tanto:
21
433
1
322
2
24
6
1000
6
3600
6
1220
6
6
1000
2
3600
2
1220
2
6
100036001220
CxC
xxx
EIy
C
xxx
yEI
x
xxyEI












Como vemos, el problema se simplifica pues sólo tenemos 3 ecuaciones y 2 constantes: C1 y C2
En consecuencia sólo necesitamos 2 condiciones iniciales.
0
24
6
1000
6
3600
6
1220
0 21
433




 2CCxC
xxx
EIy0yx
=
0
puesx
<
3
=
0
puesx
<
6

168
Cálculo de la deformación máxima en la viga:
La ecuación de la pendiente para el tramo CD es:
Por tanto:
  92567.15836
2
3600
2
1220
0
22
.x
xx



Por lo tanto:  92.5yδmaxima 
 
 
EIEI
yδmaxima
28.54056
92.567.15836
6
392.5600
6
92.512201 33
92.5 













=
(x-3)puesx
>
3
CxC
xxx
EIy0yx 21
433
24
6
1000
6
3600
6
1220
10 




=
(x-6)puesx
>
6
    .-CCEIy 6715863010
24
610
1000
6
310600
6
101220
21
433







=
(x-3)puesx
>
3
=
0
puesx
<
6
C
xxx
yEI 1
322
6
6
1000
2
3600
2
1220





=
(5.92-3)puesx
>
3
=
0
puesx
<
6
21
433
24
6
1000
6
3600
6
1220
CxC
xxx
EIy 




=
0

169
5.92xen
EI
δmaxima 
28.54056
Obviamente, el resultado es igual al obtenido sin emplear funciones de singularidad.
Caso especial
Cuando la carga distribuida no se extiende hasta el extremo derecho de la viga, se rompe la
secuencia entre las ecuaciones de los 2 últimos tramos de tal manera que la última ecuación no contiene
a la penúltima y por tanto no puede ser adoptada como ecuación representativa de la viga. Veamos la
situación y el artificio que se emplea para resolverla.




7.23.360
3.305.560
Ay
BBA
RF
KNR10RM
x.M 72

170
 5.5672  xx.M
74  x
Como se ve, la tercera ecuación no se convierte en la segunda al quitarle el último término:
 5.5672  xx.M
Para obligar a que esto ocurra se aplica el siguiente artificio que hace cambiar la forma de la
tercera ecuación de tal manera que ocurra lo requerido.
Se agregan simultáneamente las dos cargas distribuidas mostradas que al ser iguales de sentido
contrario se anulan no afectando por tanto ni las reacciones ni las fuerzas internas de la viga original.
 
2
42
72
2


x
x.M
107  x

171
La viga que estamos analizando queda por lo tanto así:
Tal como se expresó en la página anterior, las reacciones no cambian: KNR.R BA 3.372 
Los dos primeros cortes de la viga también quedan idénticos:
30  x
x.M 72
74  x
 
2
42
72
2


x
x.M
En el tercer corte, cambia la expresión del momento adoptando la forma que necesitamos:
107  x
   
2
72
2
42
72
22




xx
x.M

172
La adoptamos entonces como ecuación representativa de la viga, con los paréntesis angulares
previamente definidos:
ECUACIÓN REPRESENTATIVA DE LA VIGA:
2
72
2
42
72
22




xx
x.M
Esta ecuación la igualamos a EIy’’:
2
72
2
42
72
22




xx
x.yEI
y resolvemos el problema utilizando funciones de singularidad con todas las ventajas que se han
anotado.
4.2 MÉTODO DEL ÁREA DE MOMENTOS (TEOREMAS DE MOHR)
Como su nombre lo indica, el método utiliza los diagramas de momento flector de las vigas
Recordemos los diagramas correspondientes a alguna vigas típicas:

173
En 2 dimensiones los diagramas se ven así:
El método se basa en 2 teoremas:
El primer teorema (de Mohr) relaciona el cambio de pendiente a lo largo de la viga con el área del
diagrama de momentos entre los puntos considerados.
El teorema dice que la diferencia de pendiente entre dos puntos (por ejemplo C y D) es igual al
área de momentos entre dichos puntos dividida por la rigidez a la flexión EI.

174
El teorema establece que:
El segundo teorema (de Mohr) establece que la distancia vertical desde un punto de la elástica
hasta la tangente trazada por otro es igual al momento estático del área entre dichos puntos respecto al
primero.
El teorema establece que:
Ax
C
D 
 CD 
DdesdeMedidax:
Área del diagrama de M/EI
entre los puntos C y D

175
Demostración del Primer Teorema de Mohr
El teorema dice que la diferencia de pendiente entre dos puntos (por ejemplo C y D) es igual al
área de momentos entre dichos puntos dividida por la rigidez a la flexión EI.
Diferencia de pendiente entre dos puntos separados ddx:
La pendiente  en una viga por ser tan pequeña es igual a la derivada:

dx
dy
Por tanto:
2
2
dx
yd
dx
d

 Pero:
EI
M
dx
yd
2
2
Por lo cual:
EI
M
dx
d


y dAdx
EI
M
d 

176
  
D
C
D
C
D
C
x
x
x
x
x
x
dAdx
EI
M
d
ÁreaCD 
CD   =
lo que se quería demostrar.
Demostración del Segundo Teorema de Mohr
El segundo teorema (de Mohr) establece que la distancia vertical desde un punto de la elástica
hasta la tangente trazada por otro es igual al momento estático del área entre dichos puntos respecto al
primero.
 xdd 
  
D
C
D
C
D
C
D
C
x
x
x
x
x
x
x
x
xdAdx
EI
M
xxdd 
Pero:
C
D
D
C
x
x
d   y Axxd
D
C
x
x
  puesto que


dA
xdA
x
Por tanto: Ax
C
D  lo que se quería demostrar

177
DdesdeMedidax:
La utilidad de los 2 teoremas estriba en lo siguiente:
 Primer teorema: Sirve para calcular la pendiente en cualquier punto de la viga cuando se
conoce la pendiente en otro punto y el diagrama de momentos.
 Segundo teorema: Conocido el valor de la distancia , mediante la aplicación de algunas
relaciones de tipo geométrico y trigonométrico pueden calcularse las deformaciones  en la
viga.
El segundo teorema es especialmente útil para calcular deformaciones de vigas en voladizo
aprovechando el hecho de que la tangente a la elástica en el empotramiento es horizontal como veremos
en los ejemplos.
PROBLEMA
Calcular la deformación y la pendiente en el extremo libre del voladizo, B
El método es especialmente útil en
vigas en voladizo porque al ser la
tangente horizontal en el origen,
la deformación  es igual a la
distancia D

178
Para calcular la deformación aplicamos el segundo teorema: Ax
A
B 
Para calcular la pendiente en B aplicamos el primer teorema:
 AAB 
EI
PL
EI
PLL
A
22
2



0A
EI
PL
B
2
0
2

EI
PL
B
2
2

En resumen:
EI
PL
EI
PLL
Ax
A
B
323
2 32










EI
PL
B
3
3

3
2L
x 
(En el empotramiento
no hay giro, por
tanto la tangente es
horizontal)
EI
PL
B
2
2

EI
PL
B
3
3


179
PROBLEMA
Calcular la deformación en B y la pendiente en C Rigidez a la flexión: EI
Cálculo de la deformación en B:
Con el fin de facilitar el cálculo de las áreas y los centros de gravedad aplicamos el PRINCIPIO
DE SUPERPOSICIÓN mediante el cual podemos decir que la viga original es igual a la suma de
las dos siguientes vigas:
21 BBB  
5.212
4
3






x
23
3
2
x
EIEI
A
3
2000
2
1000
3
1







EIEI
A
3
900
3
600
2
1








180
EI
.
B
673466

Cálculo de la pendiente en C
 
EIEI
Ax
A
BB
3
5000
3
2000
5.21 





   
EIEI
Ax
A
BB
1800900
22 





 
 AAC  1
EIEI
A
3
2000
2
1000
3
1







EI
1000

EI
C
3
2000
1 
EIEI
B
1800
3
5000

21 CCC  

181
EIEI
C
800
3
2000

EI
C
67.1466

PROBLEMA
Calcular la pendiente en B y la deformación en C
EIEIEI
xA
800400
2
2
1200
2 












EI
C
800
2 
 AAC  2
EI
200

EI
400









450
4501350900
0
1350
090096
0
A
A
y
B
B
A
R
R
F
NR
R
M
BB  3tan3 
pues  es muy
pequeño

182
En la viga se observa que:
B
CBC   3
Por tanto debemos calcular B y C/B
Por tanto:
EI
EI
B
B
A 5400
66
32400





Cálculo de C/B
BB
B
A


 
6
tan
EIEI
A
8100
6
2700
2
1







46
3
2
x
EI
2700

EIEI
Ax
B
A
324008100
4 







183
Finalmente, calculamos la deformación en C recordando que:
B
CBC   3
EIEI
C
81005400
3 






EI
C
24300

Resolver con fines comparativos el siguiente problema que ya fue solucionado con el método de
la doble integración:
 
EI
A EI 4050
2
32700



23
3
2
x
EIEI
Ax
B
C
81004050
2 






Los valores de B y C/B los tomamos positivos porque se
trata de sumar dos distancias como se ve en la figura)




2003005000
300050030
Ay
BBA
RF
R5RM

184
Según la convención que hemos manejado:
EI
A
700

Ahora:  AAB 
EIEI
B
1500700







Cálculo de la deformación máxima
La clave es encontrar el punto D donde ocurre, en el cual la pendiente D es cero (pendiente
horizontal).
5
A
B
A

  2211 AxAxAx
A
B 
EIEIEIA
B
3500900
3
600
3
4

EI
A EI 600
2
2 600
1 


EI
A EI 900
2
3 600
2 


3
4
2
3
2
1 x
33
3
1
22 x
EI
EI
A
700
5
3500

EIEIEI
A
1500600900

EI
B
800


185
Como:
Cálculo de la distancia x a la cual ocurre la deformación máxima
Primer teorema: AAD 
EI
xx
A EI
x
2
200
2
2200
2 


(Distancia a la cual ocurre la deformación máxima)
  xM
R
x
A
200
200


65.2
100700
2
200700
0
2
2









x
x
EI
x
EI
A
DAmax .  652

186
La diferencia se debe a las aproximaciones
Otra forma
Aprovechándonos de que ya sabemos que en D la tangente es horizontal, tenemos:
88.0
3
65.2
1 x
EI
265200
EI
A EI 25.702
2
65.2 65.2200




EIEI
Ax
A
D
98.61725.702
88.0 
EIEI
98.617700
65.2max 






EI
02.1237
max 
65.2
3
2

EI
65.2200
EIEI
Ax
D
A
64.124025.702
65.2
3
2

EI
64.1240
max 
EI
A EI 25.702
2
65.2 65.2200




D
Amax 

187
PROBLEMA
Calcular la deformación máxima y la pendiente en los apoyos A y B de la viga:
Calculo de las pendientes:
EI
L
EI
M
8
2
max 

Por simetría la deformación
máxima se presenta en el punto
medio de la viga C.
Por lo tanto:
D
A max
Ax
C
A 
EI
L
EI
LL
C
A
384
5
2416
5 43

 
EI
L
8
2

EI
L
384
5 4
max

 
EI
L
A
24
0
3

 
AAC 
EI
L
A
24
3

 
EI
L
B
24
3

 
16
5
28
5 LL
x 
EI
L
EI
LL
A
24823
2 22



188
Por simetría: BA  
En resumen:
4.3 MÉTODO DE LA VIGA CONJUGADA
Se basa en las relaciones que existen entre la fuerza distribuida, la fuerza cortante y el momento
flector estudiadas en el curso de Mecánica y las existentes entre la curvatura, el momento flector, la
rigidez a la flexión, la pendiente, y la ecuación de la elástica estudiadas en este curso de Resistencia de
Materiales.
Recordemos las relaciones estudiadas en mecánica entre , V y M:

dx
dv
v
dx
dM

EI
L
A
24
3

 
EI
L
384
5 4
max

  EI
L
B
24
3

 

189
Y la relación estudiada en este curso:
EI
M
dx
yd
2
2
Observando estas relaciones se ingenió un artificio mediante el cual se dibuja una viga imaginaria
(VIGA CONJUGADA), apoyada y cargada de tal manera que satisfaciéndose estas relaciones se
cumplan las siguientes condiciones:
Deformación en la viga real y = Momento flector en la viga conjugada M
Pendiente en la viga real y' = Fuerza cortante en la viga conjugada
La idea es por tanto que una vez dibujada la VIGA CONJUGADA baste calcular en ella la fuerza
cortante V y el momento flector M en cualquier punto cuyos valores corresponderán a los de la
pendiente y la deformación de la viga real en los susodichos puntos.
Con el fin de dibujar la viga conjugada miremos primero que carga deberá aplicarse a la misma y
luego que apoyos deberán ponérsele.
Antes de hacerlo, recordemos los tipos de apoyo mas comunes en las vigas y los valores de la
fuerza cortante y del momento flector en los mismos.
TIPOS DE APOYOS EN VIGAS Y VALORES CORRESPONDIENTES DE PENDIENTE,
DEFORMACIÓN, FUERZA CORTANTE Y MOMENTO FLECTOR EN LOS MISMOS

190

191
TIPOS DE APOYOS EN VIGAS Y VALORES CORRESPONDIENTES DE PENDIENTE,
DEFORMACIÓN, FUERZA CORTANTE Y MOMENTO FLECTOR EN LOS MISMOS

192
De las relaciones mostradas se infiere que la relación entre los apoyos de la viga real y la viga

193
conjugada debe ser la siguiente:
Ejemplos de vigas conjugadas

194

195
PROBLEMA
Calcular la deformación y la pendiente en el extremo libre del voladizo, B
La viga conjugada es:
Por lo tanto:
EI
PL
EI
PL
BB
23
23
 
En resumen:
conjugadavigaBrealvigaB M  
conjugadavigaBrealvigaB V  
EI
PLL
F EI
PL
R
22
2



3
2L
x 
BconjugadavigaB MM 
BconjugadavigaB RV 
EI
PLL
EI
PL
M
M
EI
PL
R
F
B
B
B
y
33
2
2
0
2
0
32
2






EI
PL
B
3
3

EI
PL
B
2
2


196
PROBLEMA
Calcular la pendiente en B y la deformación en C
Dibujemos la viga conjugada:
Calculemos el momento en el empotramiento C en la viga conjugada:








450
4501350900
0
1350
090096
0
A
A
y
B
B
A
R
R
F
NR
R
M
conjugadavigaCrealvigaC M  
CconjugadavigaC MCntoempotramieelenMomentoM 
EI
F EI
2
8100
2
6 2700
1 


EI
F EI 4050
2
3 2700
2 



197
4.4 INTRODUCCIÓN A LOS MÉTODOS DE ENERGÍA
Como se dijo al principio del capítulo, aparte de los métodos matemáticos y geométricos estudiados
aquí, existen otros métodos que se estudiarán en detalle en el curso de Ingeniería Estructural I que se
basan en el principio de conservación de la energía denominados por tanto, métodos de energía.
Recordemos lo visto en el primer capítulo según lo cual cuando se aplica una carga axial gradual
a una barra dicha carga efectúa un trabajo externo que debe ser igual al trabajo interno de deformación
que se acumula en el interior de la barra y que es el que permite que la barra recupere su forma inicial
una vez retirada la carga siempre que estemos en el rango elástico lineal.
En el capítulo mencionado veíamos que para la barra de la figura el trabajo externo realizado por
la fuerza es igual a la energía acumulada en el interior de la barra.
internaexterno UW 
EI
RR
EI
-M BBA
5400
06
8100
40 
EIEIEI
MM CC
24300
2
4050
3
5400
0 
EI
RV BconjugadavigaBB
5400
 
EI
MM BconjugadavigaBB
24300
 
EI
C
24300


198
Recordemos además que el trabajo externo realizado por la fuerza es igual al área bajo la
curva P- :
Área bajo la recta=
2
P
Y encontramos que para fuerzas axiales la energía interna de deformación es:
Energía interna de deformación =
L
AE
AE
LP
22
22


De manera similar en el caso de flexión se tiene que un momento M al producir un giro d en un
cuerpo efectúa un trabajo que es igual a Md .
Por lo tanto el trabajo total será:



0
MdW
Y como el momento se aplica gradualmente, se tendrá que similarmente al caso axial en el cual
encontramos que
2
P
W  , en esta situación:
2
M
W 

199
En el curso de Ingeniería estructural se verá en detalle que la energía de deformación acumulada
en el interior de una barra cuando es flectada por un momento M es igual a:

L
EI
dxM
U
0
2
2
A partir de la aplicación del principio de conservación de la energía, en el curso mencionado se
estudiarán métodos para el cálculo de deformaciones y pendientes en vigas a través de conceptos
como el principio del trabajo y las fuerzas virtuales y de teoremas como los de Castigliano.
En Internet se encuentran muchos programas útiles para calcular deformaciones en vigas.
Recomiendoel programa DRBEAM (www.drbeam.com),por su gran utilidad didáctica enla visualización
de las deformaciones producidas en vigas con diferentes tipos de apoyos y cargas.
4.5 VIGAS ESTÁTICAMENTE INDETERMINADAS
Tal como se ha visto en capítulos anteriores, en el caso de las vigas también surgen situaciones
estáticamente indeterminadas (mayor número de reacciones que ecuaciones, por lo cual deberá seguirse
un procedimiento similar a los ya estudiados: obtener a partir de las deformaciones ecuaciones adicionales
que levanten la indeterminación).
Pero cómo surgen las vigas estáticamente indeterminadas? Veamos:
La siguiente viga como se sabe es estáticamente determinada:
Estáticamente determinada
M
F
F
A
y
x












0
0
0






y
y
x
B
A
A
Ecuaciones de
equilibrio:3
Reacciones
(incógnitas): 3

200
Al hacer el análisis deben calcularse los esfuerzos actuantes máximos  maxy max y la
deformación máxima max .
Estos valores deben ser menores que los esfuerzos y la deformación admisibles para que la viga
sea segura y funcional como se ha visto.
Sin embargo puede suceder que sean mayores (uno de ellos o todos).
En este caso el diseñador debe enfrentar varias alternativas:
a) Cambiar el material (por uno mas resistente o mas rígido según el caso).
b) Aumentar la sección transversal de la viga incrementando su resistencia y su rigidez, sin
cambiar el material.
Sin embargo enmuchas ocasiones no es posible cambiar el material o las dimensiones por problemas
de disponibilidad de otros materiales o por requerimientos arquitectónicos que no hacen posible cambiar
las dimensiones.
En estas condiciones la única alternativa para aumentar la seguridad de la viga y su rigidez será
colocar un apoyo adicional intermedio C.
Estáticamente indeterminada







y
y
y
x
C
B
A
A
M
F
F
A
y
x












0
0
0
Ecuaciones de
equilibrio:3
Reacciones
(incógnitas): 4

201
Al poner el apoyo en C se mejoran las condiciones de rigidez y resistencia de la viga:
Más RIGIDEZ (menos deformaciones) y más RESISTENCIA (más seguridad)
Lo que se gana en rigidez y en resistencia logicamente debe “pagarse” con la obtenci•n de
ecuaciones adicionales a partir de las deformaciones que levanten la indeterminaci•n.
El nuevo apoyo (que podemos llamar “redundante”), garantiza adem‚s una seguridad extra a la
viga puesto que provee a la viga con la posibilidad de mantenerse estable en caso de falla de uno de los
apoyos.
Volvamos a considerar la viga original con solamente 2 apoyos:
Veamos que sucede si se produce una falla y desaparece el apoyo B:
Observemos que si el apoyo C est‚ presente, ‡ste “acude en auxilio” de la viga para garantizar
su estabilidad. Puede ser que la viga sufra deformaciones y grietas excesivas pero el apoyo redundante
evita su colapso.
Es obvio que la viga pierde su estabilidad

202
Esta es pues, otra de las ventajas de las vigas estáticamente indeterminadas: los apoyos redundantes
garantizan la estabilidad en caso de fallas.En general, mientras mas apoyos redundantes tenga una viga
o una estructura, mas segura será. Lógicamente también tendrá un mayor grado de indeterminación y
por consiguiente el análisis será mas largo, puesto que involucrará mas ecuaciones.
Observemos como se obtiene la ecuación adicional que nos resulve la indeterminación:
Volvamos a la situación de indeterminación estática:
Estáticamente indeterminada
Para resolver el problema empleamos un artificio muy utilizado en ingeniería estructural : Quitamos
el apoyo redundante y dejamos que la viga se deforme, luego lo volvemos a poner a actuar revirtiendo
la deformación que obviamente será igual a la primera. Para el análisis empleamos el principio de
superposición asi:
Como en la situación original hay un apoyo en C, allí la deformación será cero. Por este motivo:
No sobra terminar diciendo que C1 y C2 se obtienen con cualquiera de los métodos vistos para
calcular deformaciones: El de la doble integración, el del área de momentos o el de la viga conjugada.







y
y
y
x
C
B
A
A
M
F
F
A
y
x












0
0
0
Ecuaciones de
equilibrio:3
Reacciones
(incógnitas): 4
Esta es la ecuación que levanta
la indeterminación y nos
permite resolver el problema
21 CC  
Se quita el apoyo redundante C
permitiendo que la viga se
deforme por efecto de las dos
cargas una cantidad igual a C1
Se restituye el apoyo C (o lo
que es lo mismo, la reacción
Cy) y se deja que produzca la
deformacion contraria C2

203
PROBLEMA
Calcular las reacciones en los apoyos y hacer los diagramas de fuerza cortante y momento
flector de la viga
Debemos obtener una ecuación adicional basada en la compatibilidad de deformaciones: como en
B hay un apoyo,entonces la deformación allí es igual a cero
0B
Aplicando el principio desuperposición y considerando la reacción en B como redundante, tenemos:
2 ecuaciones ESTÁTICAMENTE
3 incógnitas INDETERMINADO









-RRF
RMM
BAY
BAA
0150
05.11550
25.43
4
3
2 x
EI
A EI 5.22
3
3 5.22



Ax
A
BB   1
EIEI
B
625.955.22
25.41 






3
10
5
3
2
x
EI
A EI
RB
5.12
2
5 5



Ax
A
BB   2
EI
R
EI
R BB
B
666.415.12
3
10
2 







204
Como:
EI
R
EI
. B
BB1B
666.4162591
0 2  
Por tanto:
mKNMKNRKNR AAB  5.112.255.1158.1220.21520.2
Con estos valores, construimos los diagramas de fuerza cortante y momento flector:
Resolver el problema utilizando el método de la doble integración:
Esta es la 3a
ecuación que levanta
la indeterminación
 
56.2
8.124.382.2
2.2
3
8.12




a
aa
aa
02.2240.4
40.4
2
2.244.0
88.4
88.4
2
8.1256.2
5.11)max(







B
C
M
M
M

205
Como la carga no llega hasta el extremo derecho de la viga empleamos el artificio ya visto cuando
estudiamos funciones de singularidad:
Ecuación representativa de la viga:
2
35
2
5
22 

xx
MxRM AA
Aplicamos el método de la doble integración:
2
35
2
5
22 

xx
MxRMyEI AA
1
332
6
35
6
5
2
C
xx
xM
xR
yEI A
A



21
4423
24
35
24
5
26
CxC
xxxMxR
EIy AA



00
00


1
2
C0yx
C0yx
2 ecuaciones ESTÁTICAMENTE
3 incógnitas INDETERMINADO









-RRF
RMM
BAY
BAA
0150
05.11550
53  x

206
Ahora obtenemos la tercera ecuación que levanta la indeterminación:
875.1265.12833.20
24
25
24
55
2
5
6
5
5
4423








AA
AA
MR0
MR
00yx
Con esta y con las condiciones de equilibrio obtenemos la siguiente solución del sistema:
2.2
7.12
0.11



B
A
A
R
R
M
las cuales son sensiblemente las mismas obtenidas por superposición
PROBLEMAS PROPUESTOS
Calcular las deformaciones solicitadas en cada caso. En todos los problemas utilizar rigidez a la
flexión EI.
??  BC  MÉTODO DEL ÁREA DE MOMENTOS
??  DC  MÉTODO DE LA VIGA CONJUGADA
??  DC  MÉTODO DE LA DOBLE INTEGRACIÓN

Método de la doble integración para calcular deformaciones en vigas

Recomendados

Recomendados

Más contenido relacionado

Similar a Método de la doble integración para calcular deformaciones en vigas

Similar a Método de la doble integración para calcular deformaciones en vigas (20)

Más de jesus marcano gonzalez

Más de jesus marcano gonzalez (11)

Último

Último (20)

Método de la doble integración para calcular deformaciones en vigas