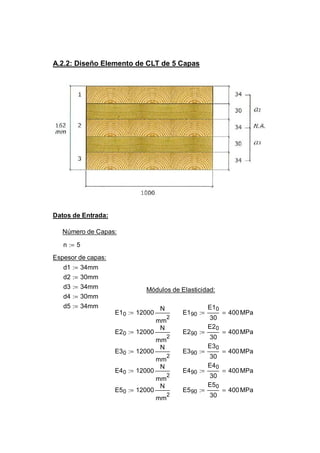
Este documento presenta el diseño de un elemento de madera contrachapada de 5 capas (CLT) sometido a carga vertical y momento flector. Se especifican las propiedades mecánicas de cada capa y las cargas aplicadas. Luego, se calculan la rigidez efectiva y las tensiones máximas en flexión del elemento mediante métodos analíticos estándar para elementos compuestos.

1. A.2.2: Diseño Elemento de CLT de 5 Capas
Datos de Entrada:
Número de Capas:
n 5:=
Espesor de capas:
d1 34mm:=
d2 30mm:=
d3 34mm:= Módulos de Elasticidad:
d4 30mm:=
d5 34mm:=
E10 12000
N
mm
2
:= E190
E10
30
400MPa=:=
E20 12000
N
mm
2
:= E290
E20
30
400MPa=:=
E30 12000
N
mm
2
:= E390
E30
30
400MPa=:=
E40 12000
N
mm
2
:= E490
E40
30
400MPa=:=
E50 12000
N
mm
2
:= E590
E50
30
400MPa=:=

2. Módulos de Corte:
G10 690MPa:= G190
G10
10
69MPa=:=
G20 440MPa:=
G290
G20
10
44MPa=:=
G30 440MPa:=
G390
G30
10
44MPa=:=
G40 440MPa:=
G490
G40
10
44MPa=:=
G50 690MPa:=
G590
G50
10
69MPa=:=
Ancho de Análisis:
b 1m:=
Solicitaciones: Transformación de Unidades:
Pmax 28897kgf:= 1kgf m⋅ 9.807J=
l 1.11m:= 1GPa 1 10
3
× MPa=
1MPa 1MPa=
Mx Pmax
l
8
⋅:=
Mx 3.932 10
4
× J=
Vx Pmax 2.89 10
4
× kgf=:=
Donde:
n = número de capas del panel.
di = espesor de la capa i del panel.
Ei = módulo de elasticidad de la capa i del panel.
Gi = módulo de corte de la capa i del panel.
b = ancho de análisis del panel, usualemente se considera b = 1m.
l = distancia entre apoyos en un ensayo en flexión, corresponde a la
longitud de la pieza, menos 7.5cm en cada extremo de ésta.

3. Solución:
a ) Determinación de distancias:
a5 d1 d2+ d3+ d4+ d5+:=
a3 d2 d3+ d4+:=
a1 d3:=
b ) Determinación coeficiente K1:
K1 1 1
E190
E10
−






a3( )3
a1( )3
−
a5( )3
⋅−:=
Tabla 5.1.a
K1 0.82=
c ) Módulo de Elasticidad Equivalente:
Eeff E10 K1⋅:=
Ec. 5.37
Eeff 9.841 10
3
× MPa=
d ) Altura de la sección:
d d1 d2+ d3+ d4+ d5+:=
d 0.162m=

4. e ) Inercia de la sección:
Ieff
b d
3
⋅
12
:=
Ieff 3.543 10
4−
× m
4
=
f ) Rigidez Efectiva:
EIeff Eeff Ieff⋅:=
Ec. 5.37
EIeff 3.487 10
6
×
m
3
kg⋅
s
2
=
g ) Tensiones máximas en flexión:
σmax
Mx
EIeff
d
2
⋅ Eeff⋅:=
σmax 8.989MPa= Ec. 5.35