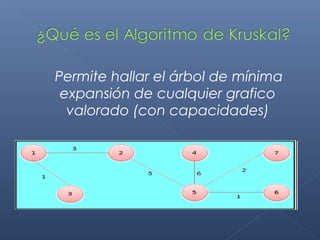
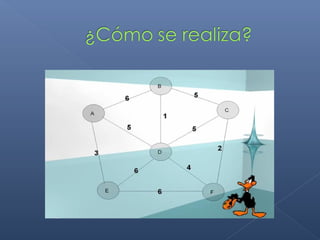
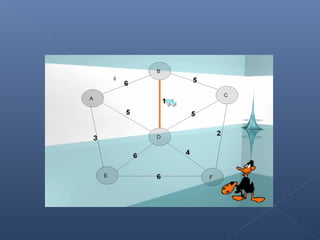
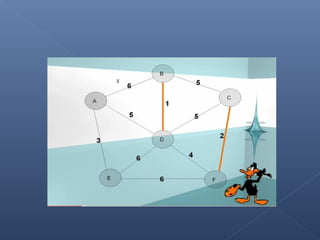
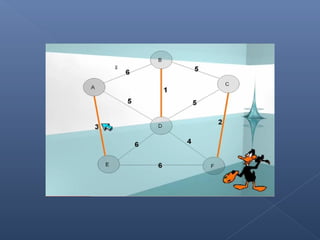
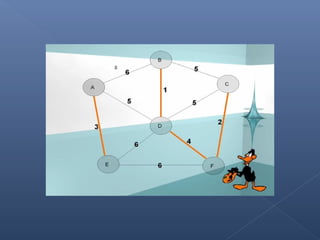
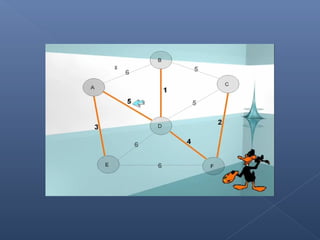
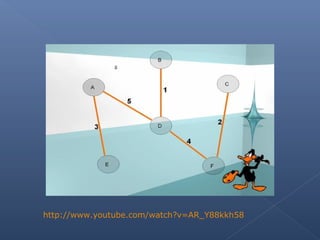
Este documento describe el algoritmo de Kruskal para encontrar el árbol de expansión mínima de un grafo valorado. El algoritmo ordena las aristas de mayor a menor peso y las va agregando al árbol si no forman ciclos, de modo que se obtiene un árbol que cubre todos los vértices con la suma mínima de pesos en las aristas.

2. Permite hallar el árbol de mínima
expansión de cualquier grafico
valorado (con capacidades)

3. Árbol de máximo alcance
cuyo valor es mínimo, es decir,
la suma de sus aristas es
mínima.

10. http://www.youtube.com/watch?v=AR_Y88kkh58

11. 1 función Kruskal (G)
2 para cada vértice v en G hacer
3 Definir un elemental grupo C (v) ← {v}.
4 Iniciar una cola de prioridad Q para contener
todas las aristas de G, usando los pesos como
claves.
5 Definición de un árbol T ← Ø / / T en última
instancia, contienen los bordes del MST
6 / / n es El Número total de vértices
7, mientras que T tiene menos de n-1 aristas hacer
8 / / u orilla, v es la ruta mínima ponderada de / v
9 (u, v) ← Q.removeMin ()

12. 10 / / ciclos previene en u SUMA T., T v en solitario si
no se contiene Una arista Que Una uy v.
11 / / Nótese QuE el grupo contiene Vértice Si Una
arista une un par
12 / / Que Han SIDO vértices añadidos al árbol.
13 Sea C (v) la v de clústeres que contiene, y sea
C (u) es el cluster que contiene u.
14 si C (v) ≠ C (u), entonces
15 Agregar borde (v, u) a T.
16 Combinar C (v) y C (u) en un clúster, es decir, la
unión C (v) y C (u).
17 T retorno árbol

13. kruskalMST(G,n,F)
Construir una cola de prioridad cp con los lados;
Inicializar componente conexa;
F=0;
while ((vacia(cp) != false) && (jFj < n - 1))
arista = obtenerMin(cp);
borrarMin(cp);
u = Componente(De(arista));
v = Componente(A(arista));
if (NumeroComponente(u) !=
NumeroComponente(v))
a~nadir arista a F;
unirComponentes(u,v);