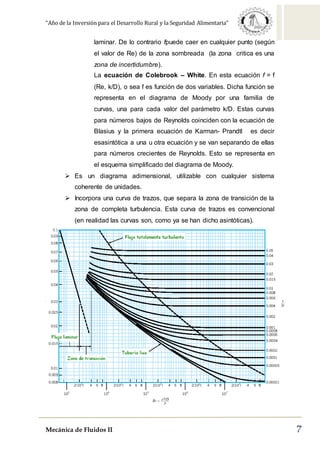
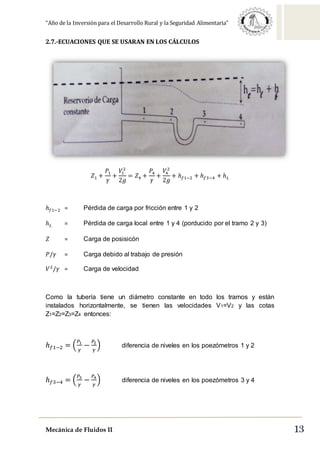
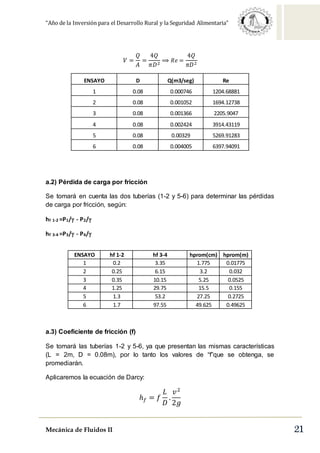
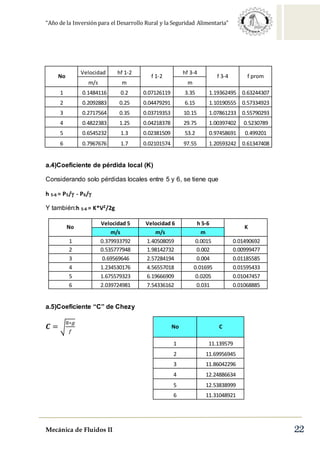
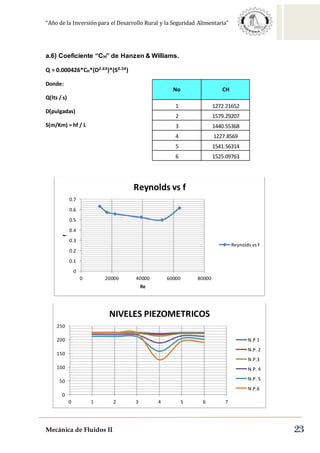
Este documento describe la pérdida de carga en tuberías. Explica las pérdidas primarias y secundarias, y presenta la ecuación de Darcy-Weisbach para calcular las pérdidas primarias. También describe el diagrama de Moody, que relaciona el coeficiente de fricción con el número de Reynolds y la rugosidad relativa, y explica cómo se puede usar para determinar el régimen de flujo. Además, explica brevemente el tubo de Venturi y cómo puede usarse para medir caudales.