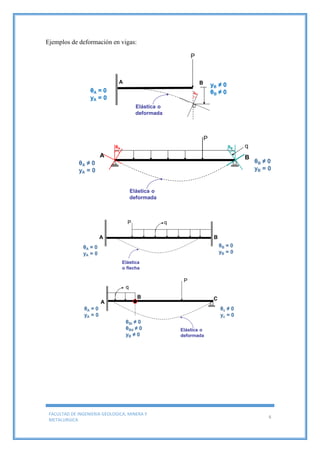
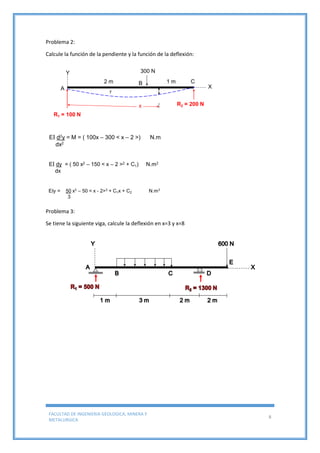
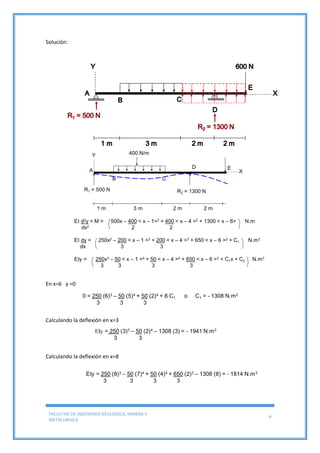
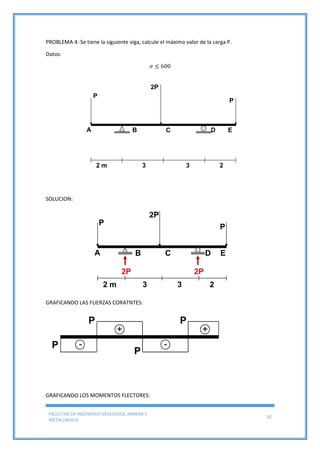
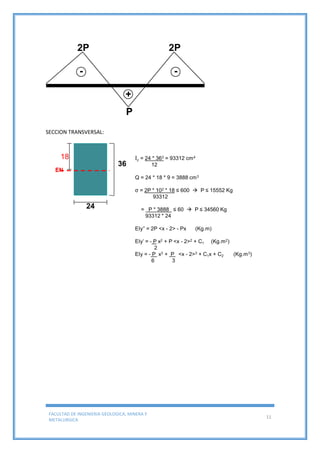
Este documento trata sobre la deflexión de vigas y presenta varios ejemplos y problemas resueltos. Explica el método de doble integración para determinar deflexiones en vigas sometidas a diferentes cargas y condiciones de apoyo. Además, concluye que la deflexión de vigas es importante en el diseño de estructuras y depende de factores como la distancia entre apoyos, el material, la carga y las propiedades geométricas de la viga.

1. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
1
DEFLEXION DE VIGAS
DURAND PORRAS, JUAN CARLOS (PROFESOR ASESOR)
GAMARRA CORILLCOLLA, DIEGO
GONZALES ANGULO, JHONNATAN
HUERTA ESPINOZA, PÉTER HERLY
UNIVERSDAD NACIONAL DE INGENIERIA
I. RESUMEN:
Los objetivos de esta investigación es dar a conocer el tema de deflexión de vigas y sus
aplicaciones en la ingeniería; este trabajo se realizó tras una exhaustiva investigación,
consultando distintas fuentes de información.
Con el desarrollo del presente trabajo se llegó a resultados que nos permitieron formular
posibles soluciones a los distintos problemas en el diseño de una construcción.

2. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
2
II. INDICE:
PÁGINA
RESUMEN 1
INDICE 2
INTRODUCCION 3
DESARROLLO DEL TEMA 4
RESULTADOS 7
CONCLUSIONES 13
REFERENCIAS 14

3. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
3
III. INTRODUCCIÓN:
Como bien se sabe hoy en día, en las distintas obras de construcción es de
suma importancia la seguridad, es por tal motivo que los profesionales deben
realizar un buen diseño y análisis de los distintos comportamientos que va a
tener una viga, para luego garantizar que esta construcción sea segura y evite
cualquier tipo de accidentes fatales, por este motivo hemos creído conveniente
realizar este trabajo que se trata de la deflexión en vigas, siendo un tema de
vital importancia para las distintas construcciones.

4. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
4
IV. DESARROLLO DEL TEMA:
Para comenzar este tema se debe recordar la ecuación en la cual se relaciona
la curvatura de la superficie neutra con el momento flector en una viga
sometida a flexión pura:
1
𝜌
=
𝑀(𝑥)
𝐸. 𝐼
Donde ‘ρ’ es el radio de curvatura, ‘E’ el módulo de elasticidad del material
del que se compone la viga, ‘I’ el momento de inercia de la sección transversal
de la viga y ‘M(x)’ el momento flector al que está sometida la misma.
Observemos que este último término se ha designado como dependiente de la
longitud medida desde un extremo de la viga (‘x’).
METODO DE DOBLE INTEGRACIÓN:
Es el más general para determinar deflexiones. Se puede usar para resolver
casi cualquier combinación de cargas y condiciones de apoyo en vigas
estáticamente determinadas e indeterminadas. Su uso requiere la capacidad de
escribir las ecuaciones de los diagramas de fuerza cortante y momento flector
y obtener posteriormente las ecuaciones de la pendiente y deflexión de una
viga por medio del cálculo integral. El método de doble integración produce
ecuaciones para la pendiente la deflexión en toda la viga y permite la
determinación directa del punto de máxima deflexión.
A una distancia “x” del origen “o”, la sección de estudio de la viga, por efecto de las
cargas que actúan sobre ella, experimenta dos tipos de deformaciones:
θ: Giro de la sección o deformación angular
y: Flecha de la sección, también denominado desplazamiento lineal

5. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
5
En la sección de estudio, en su configuración deformada:
𝑇𝑔𝜃 =
𝑑𝑦
𝑑𝑥
= 𝜃 (Por ser “θ” pequeño)
Luego: θ =
𝑑𝑦
𝑑𝑥

𝑑θ
𝑑𝑥
=
𝑑2 𝑦
𝑑𝑥2
Esta ecuación se denomina, ecuación diferencial del eje deformado de la viga o
simplemente: elástica
𝐸𝐼
𝑑2
𝑦
𝑑𝑥2
= 𝑀
Al producto EI, se le llama rigidez a la deformación por flexión.
Ecuación diferencial con variables separables, la solución es:
Primera integración:
𝐸𝐼
𝑑𝑦
𝑑𝑥
= ∫ 𝑀𝑑𝑥 + 𝐶1 ; Como:
𝑑𝑦
𝑑𝑥
=θ
𝐸𝐼𝜃 = 𝑀𝑑𝑥 + 𝐶1 Ecuación de giros
Segunda integración:
𝐸𝐼𝑦 = ∫ 𝑀𝑑𝑥𝑑𝑥 + 𝐶1𝑥 + 𝐶2 Ecuación de la elástica
Las constantes C1 y C2, se obtienen de la condición de bordes o extremos de la viga

6. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
6
Ejemplos de deformación en vigas:

7. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
7
V. RESULTADOS DEL ESTUDIO:
Los resultados de la investigación se observa en las siguientes soluciones de
estos ejemplos:
Problema 1:
Para la viga mostrada, calcular la flecha máxima en el tramo BC:

8. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
8
Problema 2:
Calcule la función de la pendiente y la función de la deflexión:
Problema 3:
Se tiene la siguiente viga, calcule la deflexión en x=3 y x=8

9. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
9
Solución:
En x=6 y =0
Calculando la deflexión en x=3
Calculando la deflexión en x=8

10. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
10
PROBLEMA 4: Se tiene la siguiente viga, calcule el máximo valor de la carga P.
Datos:
𝜎 ≤ 600
SOLUCION:
GRAFICANDO LAS FUERZAS CORATNTES:
GRAFICANDO LOS MOMENTOS FLECTORES:

11. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
11
SECCION TRANSVERSAL:

12. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
12

13. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
13
VI. CONCLUSIONES:
Como se observa la deflexión de vigas es un tema importante en el diseño de
estructuras.
Se observa que un el tema de deflexión de vigas se puede aplicar:
 En estructuras metálicas
 Sistemas de tuberías
En el estudio de una viga, esta puede flectar de acuerdo a ciertos factores que
son los siguientes:
 Distancia entre apoyo
 Material de la viga
 La carga aplicada
 Propiedades geométricas de la viga
 Tipos de vinculación (apoyos)

14. FACULTAD DE INGENIERIA GEOLOGICA, MINERA Y
METALURGICA
14
VII. REFERENCIAS:
RIVERA BERRIO, Juan Guillermo (2010). DIAGRAMAS DE MOMENTO FLECTOR Y
AAAACORTANTE. DESCARTES - Ministerio de Educación, Cultura y Deporte de España.