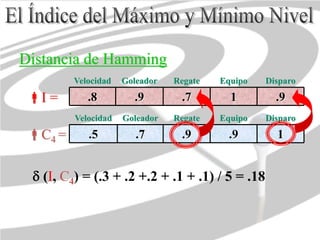
El documento introduce los conceptos de incertidumbre, probabilidad y vaguedad. Explica que la probabilidad mide la frecuencia de resultados de experimentos aleatorios, mientras que la vaguedad se refiere a límites imprecisos relacionados con el lenguaje humano. También discute formas de representar y cuantificar la incertidumbre, incluidos los conjuntos difusos, redes bayesianas y la subjetividad en la calificación de eventos.




















![Subconjunto Borroso A
a b c d e f g
A = 0.4 0.5 1 0.7 0.2 0.5 0.6
μ (x) = [0, 1]
¿Qué es un Número Borroso?](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-21-320.jpg)










![Intervalo de Confianza
A = [a1, a2]
[min, max]
0
1
0 1 2 3 4 5 6 7 8
[ ]
A = [2, 8]](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-32-320.jpg)
![Tripleta de Confianza
A = (a1, a2 , a3)
(min, m. pres.,max)
0
1
0 1 2 3 4 5 6 7 8
[ ]
A = (2, 3, 8)
•](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-33-320.jpg)
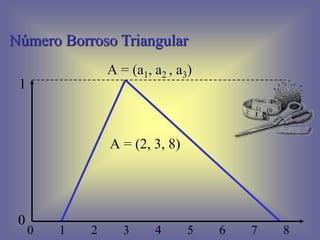
![Cuádruplo de Confianza
A = (a1, a2 , a3 , a3)
0
1
0 1 2 3 4 5 6 7 8
[ ]
A = (2, 3, 4, 8)
• •](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-35-320.jpg)
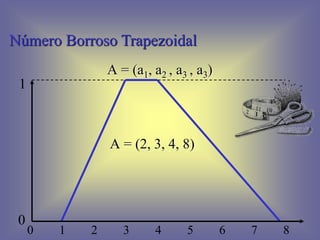
![Intervalos de Confianza
Suma de Intervalos de Confianza
[a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2]
[2, 3] (+) [1, 4] = [2 + 1, 3 + 4] = [3, 7]
Sustracción de Intervalos de Confianza
[a1, a2] (-) [b1, b2] = [a1 – b2, a2 – b1]
[2, 3] (-) [1, 4] = [2 - 4, 3 - 1] = [-2, 2]
Normal](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-37-320.jpg)
![Intervalos de Confianza
Suma de Intervalos de Confianza
[a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2]
[2, 3] (+) [1, 4] = [2 + 1, 3 + 4] = [3, 7]
Sustracción de Intervalos de Confianza
Minkowsi
[a1, a2] (m) [b1, b2] = [a1 – b1, a2 – b2]–
[2, 3] (m) [1, 4] = [2 - 1, 3 - 4] = [-1, 1]–
[min, max]](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-38-320.jpg)
![Intervalos de Confianza
Producto de Intervalos de Confianza
[a1, a2] (•) [b1, b2] =
[2, 3] (•) [1, 4] =
[Min {a1•b1, a1•b2, a2•b1, a2•b2}, Max {a1•b1, a1•b2, a2•b1, a2•b2}]
[Min {2 • 1, 2 • 4, 3 • 1, 3 • 4}, Max {2 • 1, 2 • 4, 3 • 1, 3 • 4}]
[Min {2, 8, 3, 12}, Max {2, 8, 3, 12}] = [2, 12]](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-39-320.jpg)
![Intervalos de Confianza
División de Intervalos de Confianza
[a1, a2] (:) [b1, b2] =
[2, 3] (:) [1, 4] =
[Min {a1/b1, a1/b2, a2/b1, a2/b2}, Max {a1/b1, a1/b2, a2/b1, a2/b2}]
[Min {2/1, 2/4, 3/1, 3/4}, Max {2/1, 2/4, 3/1, 3/4}]
[Min {.5, .5, 3, .25}, Max {.5, .5, 3, .25}] = [.25, 3]](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-40-320.jpg)













![Experto A: A = [.1, .2];
Experto B: B = [.7,
.9];Experto C: C = [.8, .9];
Experto D: D =
1;Experto E: E = [.5,
.9];Experto F: F = [.5,
.6];Experto G: G = [.4,
.7];Experto H: H = [.6,
.7];Experto I: I = .8;
Experto J: J = .5.
1
3
1
2
1
1
1
1
2
1
1
3
1
1
0
.1
.2
.3
.4
.5
.6
.7
.8
.9
1
Estadística
La Agregación de Expertos](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-54-320.jpg)

![.1
.4
.5
.7
.8
.9
1
.1
.1
.3
.4
.5
.8
.9
.9
.9
1
10
.1
.2
.3
.4
.5
.6
.7
.8
.9
1
Expertón
La Agregación de Expertos
Esperanza Matemática
de un Expertón:
(A) = [.59, .72].
(A) =.](https://image.slidesharecdn.com/lgicadifusa-130806085007-phpapp01/85/LOGICA-DIFUSA-56-320.jpg)