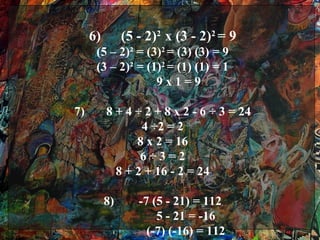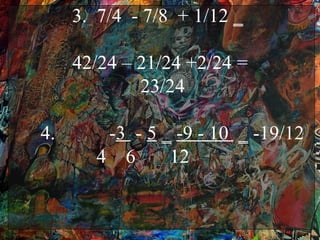Este documento presenta los conceptos básicos de los números reales en la unidad 1 de un curso de álgebra. Explica las propiedades y operaciones de los números enteros, racionales y valor absoluto, incluyendo la suma, resta, multiplicación y división. También cubre temas como el orden de operaciones y la simplificación de fracciones. El documento proporciona ejemplos para cada concepto y enlaces a videos de YouTube para una explicación más detallada.

1. Math 2301
Algebra
Unidad 1
Números Reales

2. Unidad 1: Números Reales
• Comenzaremos a mencionar los
números reales: sus propiedades y
leyes. Estas nos servirán de
herramienta para entender los
conceptos algebraicos.
• El conjunto de enteros no negativos los
identificamos como:
W = {0, 1, 2, 3, . . .}

3. Ejemplo: 5 + 9 = 9 + 5
Sección 1.1
Suma de enteros no negativos:
Para dos enteros no negativos cualesquiera a y b
existe un entero no negativo único llamado su
suma. La suma de a y b es a + b.
Ahora vamos a presentar las leyes de la suma de
enteros no negativos.
· Ley Conmutativa de la suma
a + b = b +a
Ejemplo: 5 + 9 = 9+5

4. Ley Asociativa de la Suma
a + ( b +c ) = (a +b) + c
Ejemplo: 5 + ( 4 + 3) = ( 5 + 4 ) + 3
Elemento Identidad para la suma
El cero es el elemento identidad aditivo.
a+0=0+a=a
Ejemplo: 4 + 0 = 0 + 4 = 4

5. Secc. 1.2
Multiplicación de enteros no negativos
El producto de dos enteros no negativos
a y b se define como el entero no negativo a . b
que representa la suma b + b + b + . . . + b
a términos iguales a b.

6. Multiplicación por cero
ax0=0
Ejemplo: 5 x 0 = 0
Ley conmutativa de la Multiplicación
ab = ba
Ejemplo: (5)(3) = (3)(5)

7. Ley Asociativa de la Multiplicación
a (b . c) = (a . b) c
Elemento Identidad para .la multiplicación
Ejemplo: 5 (3 4) = (5 . 3) 4
El uno se denomina como identidad multiplicativo.
ax1=1xa=a
Ejemplo: 5 x 1 = 1 x 5 = 5

8. Ley Distributiva de la
multiplicación sobre la suma.
(b + c) a = a ( b + c) = ab + ac
Ejemplo: (5 + 3) 2 = 2 (5 + 3) =
2x5 + 2x3

9. Números Enteros - es la combinación de
los enteros negativos y de los enteros no
negativos.
I = {. . . , -3, -2, -1, 0, 1, 2, 3, …}
Ahora pasamos a ver las reglas de estos
números llamados enteros negativos y
enteros no negativos.

10. Para entender mejor el concepto
de los Números Enteros debes
accesar a la siguiente dirección de
YOUTUBE:
http://www.youtube.com/watch?v=Vtd8_XmJPE4&featu

11. Secc. 1.3
Suma de números enteros
Si tienen signos iguales, se suman y
se usa el signo en común. Si tienen
signos diferentes, se restan y se usa
el signo del número mayor.

12. Ejemplos:
(-5) + (-3) = -8
(15) + (-7) = 8
(-20) + (3) = -17
(-11) + 6 = -5
(-3) + (-2) + (12) = 7
(7) + (2) = 9

13. Sección 1.4
Resta de números enteros
Se le cambia el signo del sustraendo y se
procede a sumar, o sea, que usamos las reglas
que vimos para la suma de números enteros.
Ejemplos:
(4) - (-3) = (4) + (3) = 7
(-5) - (2) = (-5) + (-2) = -7
(8) - (6) = (8) + (-6) = 2
Restar -6 de 4 es (4) - (-6) = 4 + 6 = 10
(-10) - (3) = (-10) + (-3) = -13

14. Sección 1.5
Multiplicación de números enteros
Si tienen signos iguales el resultado de la
multiplicación, llamado producto, va a
ser un número positivo.
Si tienen signos diferentes el resultado va
a ser un número negativo.

15. Ejemplos:
(5) (-6) = -30
(-3) (-4) =12
(-8) (3) = -24
(7) (2) = 14
(3) (2) (-4) (-1) = 24
(-3) (-8) (-2) = -48
(2) (-8) (0) (-3) = 0

16. Sección 1.6
División de los números enteros
Se aplican las mismas reglas que en la
multiplicación de números enteros.
Signos iguales resultado positivo, signos
diferentes resultado negativo.

17. Ejemplos:
(40) ÷ (-5) = -8
(-70) ÷ (-10) = 7
(-50) ÷ (2) = -25
(15) ÷ (3) = 5
-100 = 5
-20
0= 0
8
8 = No definido
0

18. Para entender mejor la suma, resta,
multiplicación y división de los Números
Enteros debes accesar a las siguientes
direcciones de YOUTUBE:
http://www.youtube.com/watch?v=qHdUDPqyrxI&feature=related
http://www.youtube.com/watch?v=r0_Y30yg80k&feature=related

19. Sección 1.7
Otra parte importante par entender bien los procesos
algebraicos es estudiar el tema: Orden de Operaciones.
Cuando vamos a realizar un ejercicio en matemática tenemos
que seguir un orden que será:
1) Eliminar símbolos de agrupación de adentro hacia
fuera del ejercicio.
2) Resolver las potencias o toda aquella expresión que
contenga exponentes.
3) Resolver la multiplicación y la división de izquierda a
derecha o lo primero que aparezca.
4) Resolver la suma y la resta de izquierda a derecha.

20. Ejemplos:
1) 12 x 5 ÷ 3 x 2 = 40
12 x 5 = 60
60 ÷ 3 = 20
20 x 2 = 40
Este ejercicio tiene las operaciones de multiplicación
y división, por lo tanto, las realizamos en el orden en
que aparecen.

21. 2) 11 - 3 x 2 = 5
3x2=6
11- 6 =5
3) 32 x 7 - 2³ ÷ 4 = 61
32 = (3) (3) =9
23 = (2) (2) (2) = 8
9 x 7 = 63
8÷4=2
63 - 2 = 61

22. 4) 56 ÷ 8 + 3 x 2 = 13
56 ÷ 8 = 7
3x2=6
7 + 6 = 13
5) 3 + 4 (5 + 2) = 31
5+2=7
4 x 7 = 28
3 + 28 = 31

23. 6) (5 - 2)2 x (3 - 2)2 = 9
(5 – 2)² = (3)2 = (3) (3) = 9
(3 – 2)² = (1)2 = (1) (1) = 1
9x1=9
7) 8 + 4 ÷ 2 + 8 x 2 - 6 ÷ 3 = 24
4 ÷2 = 2
8 x 2 = 16
6÷3=2
8 + 2 + 16 - 2 = 24
8) -7 (5 - 21) = 112
5 - 21 = -16
(-7) (-16) = 112

24. Para entender mejor el tema de Orden de
Operaciones debes accesar a las siguintes
direcciones de YOUTUBE:
http://www.youtube.com/watch?v=jdcxyjLxHfY
http://www.youtube.com/watch?v=Y3CZ_JBQ0do
http://www.youtube.com/watch?v=Zdv-oBbLp0E

25. Sección 1.8
Uno de los temas que debemos repasar
para también entender las operaciones
algebraicas es el tema:
Números Racionales o Fracciones.
En casi todos lo temas de algebra las
fracciones están presentes, es por eso que
debemos repasar los conceptos básicos.

26. A. Simplificación Fracciones:
1. 24 ‗ 2/3
36
Se simplifica con el 12 por lo tanto:
24 ÷ 12 ‗ 2
36 12 3

27. 2. -12 ‗ - 2/5
30
3. 21 ‗ 3/5
35
4. 8 ‗ 8 ‗ 4/5
12-2 10
5. 18 - 20 ‗ -2 ‗ - 1/4
3+5 8

28. 6. -8 - 10 ‗ -18 ‗ 3
6 - 12 -6
7. 20 + 7 ‗ 27 ‗ - 9/2
-6 -6

29. B. Suma y Resta Fracciones
1. 1/7 + 4/7 = 5/7
2. 8/9 - 1/9 + 3/9 = 10/9

30. 3. 7/4 - 7/8 + 1/12 ‗
42/24 – 21/24 +2/24 =
23/24
4. -3 - 5 ‗ -9 - 10 ‗ -19/12
4 6 12

31. Para repasar la suma y resta de
fracciones deberás accesar a las
siguientes direcciones de
YOUTUBE:
http://www.youtube.com/watch?v=JUEson1cpyo
http://www.youtube.com/watch?v=5vf9lOgKuXI&featur

32. C. Multiplicación y División Fracciones
1. 3 x 7 ‗ 21 ‗ 7/24
4 18 72
1
2
2. 6 x 14 x 15 ‗ 1,260 ‗ 1/2
35 9 8 2,520

33. 3. -12 ÷ 32 ‗ -12 x 14 ‗ -168 ‗ -1/4
21 14 21 32 672
4. 24 x 49 ÷ 21 =
35 32
24 x 49 x 1 ‗ 1,176 ‗ 1/20
35 32 21 23,520

34. 5. 1 + 16 x 3 ‗
6 9 4
16 x 3 ‗ 48 ‗ 4
9 4 36 3
1 + 4 ‗ 1 + 8 9 ‗ 3/2
6 3 6 6

35. Para entender mejor la multiplicación y
división de fracciones debes accesar a las
direcciones a continuación de
YOUTUBE:
http://www.youtube.com/watch?v=Mnu16kCRW4U
http://www.youtube.com/watch?v=heo7-qXbl0M

36. Secc. 1.9
Valor Absoluto – es la distancia que está un
punto de origen. Siempre se expresa en forma
positiva.
│- 6 │= 6
│2 – 11│= │- 9 │= 9
│-11 -4 │ = │-15 │ = 15

37. •- │ - 5 │= -5
-│3 │= -3
-│3 │= -3
-│-5 │= -5

38. Para entender mejor el tema de Valor
Absoluto deberás accesar a la siguiente
dirección de YOUTUBE:
http://www.youtube.com/watch?v=Nv57kGxhiIc

39. REALIZAR
EJERCICIO
#1