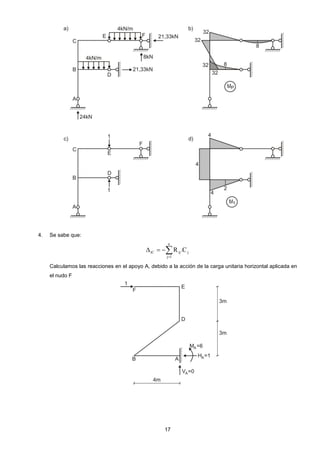
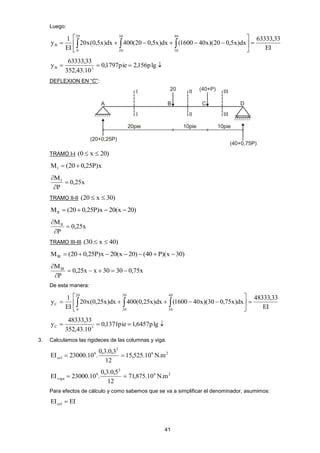
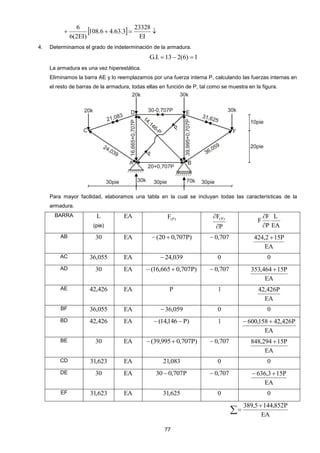
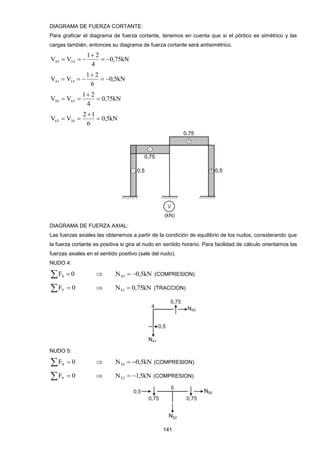
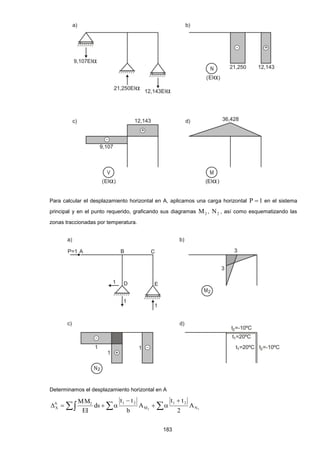
Este documento presenta las prácticas calificadas y exámenes resueltos correspondientes al curso de Resistencia de Materiales II dictado en la Universidad de San Martín de Porres entre 2008 y 2010. El libro contiene la resolución de problemas aplicados utilizando los métodos del trabajo virtual, energía de deformación, teoremas de Castigliano, método de las fuerzas y método de desplazamientos. El objetivo es facilitar el aprendizaje individual de los estudiantes mediante la solución detallada de los ejercicios propuestos