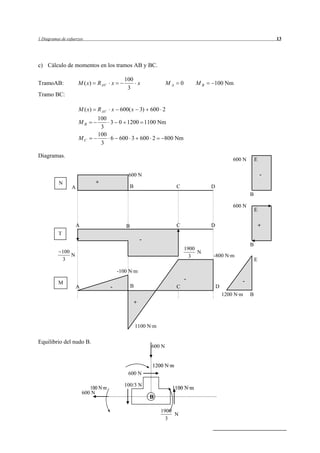
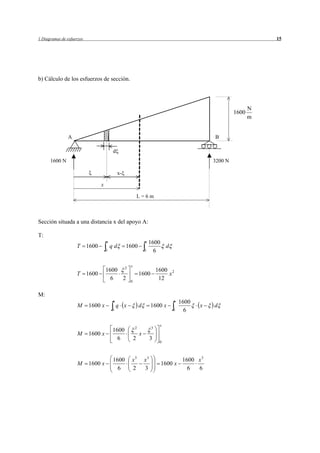
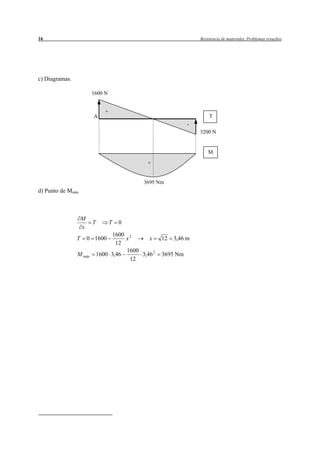
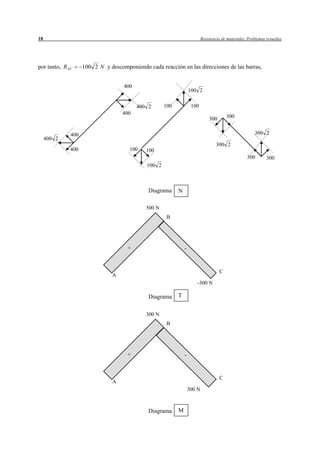
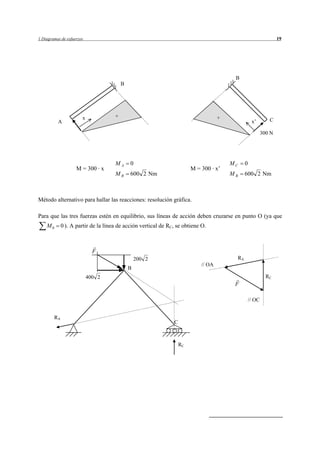
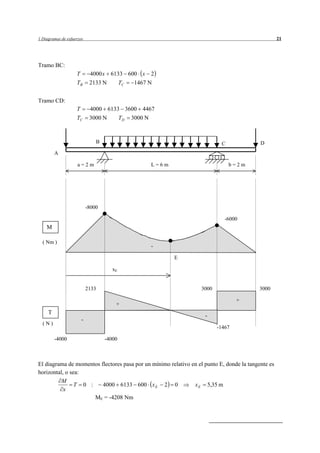
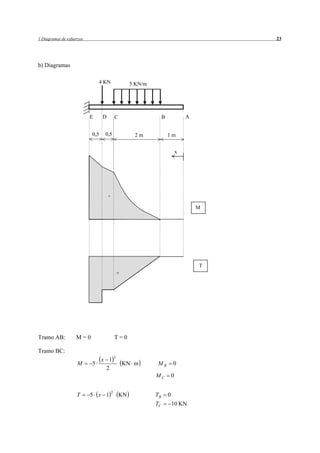
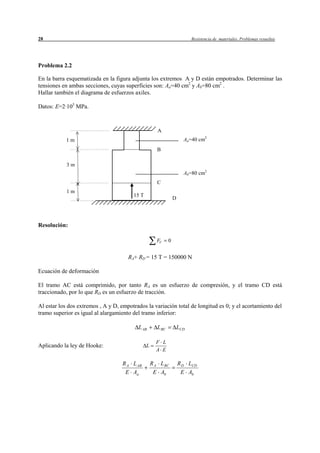
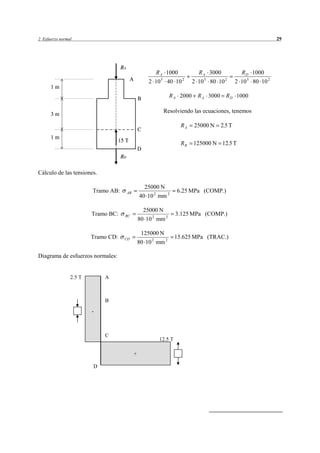
Este resumen describe el problema 1.1 del documento. Se trata de determinar los diagramas de esfuerzos en una estructura compuesta por barras sometida a fuerzas externas. Se realizan los pasos de descomponer las fuerzas externas, calcular las reacciones, los momentos en los tramos y los diagramas de esfuerzos resultantes.

1. 12 Resistencia de materiales. Problemas resueltos
Problema 1.1
Determinar los diagramas de esfuerzos en la estructura de la figura.
600 2 2
˜
600 2 2
F
H
F
A
Resolución:
a) Descomposición de la fuerza exterior aplicada en el extremo de la barra BE.
b) Cálculo de las reacciones.
Tomamos momentos respecto al punto C:
¦Mc 0 Ÿ 6 600 3 600 2 800 0 100
N = -33,3 N
3
RAV ˜ ˜ ˜ Ÿ RAV
Suma de fuerzas verticales y horizontales:
N
600 1900
3
¦ FV 0 Ÿ RAV 600 RCV 0 Ÿ 100 RCV
3
¦FH 0 Ÿ RAH 600 N
600 N
2
600 N
2
˜
V
Ejes globales
B
C
E
D
600 2 N
45o
3 m 3 m 2 m
2 m
800 Nm
A
B
C
E
D
600 N
600 N
RAV
RAH RCV
800 Nm

2. 1 Diagramas de esfuerzos 13
c) Cálculo de momentos en los tramos AB y BC.
( ) ˜ 100 ˜ M x RAV x x M A MB
TramoAB: 0 100 Nm
3
Tramo BC:
Diagramas.
M x R x x
( ) ˜ 600( 3) 600 ˜
2
˜
B
M
A B C D
100
Equilibrio del nudo B.
6 600 3 600 2 800 Nm
100
100
3
3 0 1200 1100 Nm
3
˜ ˜ ˜
C
AV
M
600 N
600 N
-
600 N
600 N
1900 N
3
B
100/3 N
B
E
+
A B C D
600 N
A B C D
B
E
-
-
+
1200 N·m
-100 N·m
-800 N·m
B
E
+
600 N
1900
3
N
-
N
T
M
1100 N·m
-
N
3

3. 14 Resistencia de materiales. Problemas resueltos
Problema 1.2
Determinar los diagramas de esfuerzos en la viga de la figura, apoyada en los extremos y sometida a
una carga repartida triangular.
A B
Resolución:
a) Cálculo de la reacciones.
1600 6
6 m
Resultante de la carga 4800 N
2
˜
Q .
4800 N
A B
RA RB
4 m 2 m
R R
¦
6 m
0 6 4800 4
A B
4800 4
1600 N
3200 N
6
4800
˜
Ÿ ˜ ˜
B
A
A B
R
R
M R
x
1600 N
m
T
6

4. 1 Diagramas de esfuerzos 15
b) Cálculo de los esfuerzos de sección.
A B
L = 6 m
d[
Sección situada a una distancia x del apoyo A:
T:
[ [ [
2
x x
1600 1600 1600
³ ³
T q d d
0 0
x
0
2
1600 1600
12
ª
1600 1600
˜
6 2
6
º
T x
»¼
«¬
[
M:
x x
1600 1600 1600

6. ³ ˜ ³ ˜
M x q x d x x d
[ [ [ [ [
0 0
x
0
1600 1600
6 6
ª
1600 1600
2 3
§
M x x
˜
6 2 3
§
1600 1600
§
˜
6 2 3
6
·
·
·
º
3 3 3
M x x x x x
˜ ¸¸
¹
¨¨
©
¸¸¹
¨¨©
¨¨©
»»¼
««¬
¸¸¹
[ [
x
1600 N
m
1600 N 3200 N
[ x-[

7. 16 Resistencia de materiales. Problemas resueltos
c) Diagramas.
d) Punto de Mmáx
A T
Ÿ
M
T x x
o
3,46 3695 Nm
0
0 1600 1600
1600 3,46 1600
12
12 3,46 m
12
2
máx
2
˜ ˜
w
w
M
T T
x
1600 N
3695 Nm
3200 N
-
M
+
+

8. 1 Diagramas de esfuerzos 17
Problema 1.3
Determinar los diagramas de esfuerzos del pórtico inclinado de la figura.
Resolución:
200 2 N
400 2 N
45q
Para el cálculo de las reacciones, planteamos las ecuaciones de la estática.
F R R
RAH
0 200 2 0
Ÿ
V AV C
F R
0 400 2 N
Ÿ
H AH
M R R
0 4 400 2 2 200 2 2 0 300 2 N
Ÿ ˜ ˜ ˜ Ÿ
¦¦¦
A C C
2 m
2 m 2 m
C
B
A
200 2
400 2
C
B
A
RAV RC

9. 18 Resistencia de materiales. Problemas resueltos
por tanto, RAV 100 2 N y descomponiendo cada reacción en las direcciones de las barras,
400 2
Diagrama
Diagrama
Diagrama
400
400
400
400
400 2
100 100
100 100
100 2
100 2
300 300
300 300
300 2
300 2
N
+ -
C
A
B
500 N
-300 N
T
+ -
C
A
B
300 N
300 N
M

10. 1 Diagramas de esfuerzos 19
x +
M = 300 · x
0
600 2 Nm
B
A
M
B
M
M = 300 · x’
0
600 2 Nm
C
M
B
M
A
Método alternativo para hallar las reacciones: resolución gráfica.
Para que las tres fuerzas estén en equilibrio, sus líneas de acción deben cruzarse en punto O (ya que
0 0 ¦M ). A partir de la línea de acción vertical de RC, se obtiene O.
C
B
300 N
x’
+
200 2
G
400 2
C
B
RA
RC
F
RA
G RC
F
// OA
// OC

11. 20 Resistencia de materiales. Problemas resueltos
Problema 1.4
Determinar los diagramas de esfuerzos en la viga de la figura.
p = 600
N
ml
4000 N 3000 N
Resolución:
Cálculo de las reacciones:
M R R
: 4000 2 600 6 3 6 3000 8 4467 N
6133 N
: 4000 600 6 3000 0
˜ ˜ ˜ ˜ ˜ Ÿ
˜
¦
¦
B C C
B
V B C
R
F R R
Diagrama de momentos flectores:
Tramo AB:
M x
4000
˜
M A MB
0 8000 Nm
Tramo BC:

13. M x x x
4000 6133 2 600 2
8000 Nm 6000 Nm
2
2
˜ ˜ ˜
MB MC
Tramo CD:

16. M x x x x
4000 6133 2 600 6 5 4467 8
˜ ˜ ˜ ˜ ˜
MC 6000 Nm MD
0
Diagrama de esfuerzos cortantes.
Tramo AB:
4000 N
TA TB
4000 N 4000 N
T
P1
A
B C P2 D
a = 2 m L = 6 m b = 2 m

17. 1 Diagramas de esfuerzos 21
Tramo BC:

18. T x x
˜
TB TC
4000 6133 600 2
2133 N 1467 N
Tramo CD:
4000 6133 3600 4467
TC TD
3000 N 3000 N
T
T
El diagrama de momentos flectores pasa por un mínimo relativo en el punto E, donde la tangente es
horizontal, o sea:
0 : 4000 6133 600 ˜ 2

19. 0 Ÿ 5,35m
M
w
w
T xE xE
x
ME = -4208 Nm
D
-8000
-6000
2133
-4000 -4000
3000 3000
-1467
M
( Nm )
( N )
-
-
-
+
+
E
xE
A
B C
a = 2 m L = 6 m b = 2 m

20. 22 Resistencia de materiales. Problemas resueltos
Problema 1.5
En la viga en voladizo de la figura, calcular las reacciones en el empotramiento y dibujar los
diagramas de esfuerzos cortantes y de momentos flectores en toda la viga.
Resolución:
4 KN
0,5m
5 KN/m
1 m 2 m 1 m
a) Reacciones en el empotramiento.
Comenzaremos por buscar el sistema de fuerzas que ejerce el empotramiento, dibujamos el diagrama
de sólido libre y obligamos al equilibrio. Sumando fuerzas y tomando momentos obtenemos:
¿¾½
4 KN
0.5m
14 KN
˜ ˜ ˜
4 0,5 10 2 22 KN m
E
M
E
F
4 KN
2 m
0.5m
FE
10 KN
ME
Reacciones que ejerce el empotramiento sobre la viga.
1 m 2 m
FE
ME
5 KN/m