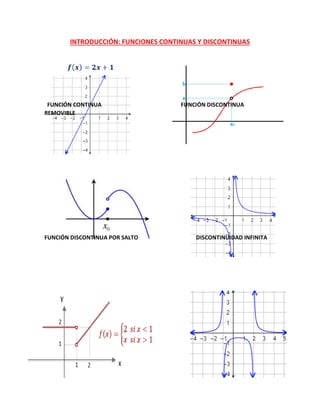
Este documento introduce los conceptos de funciones continuas y discontinuas, y luego define el límite de una función. Explica que el límite de una función f(x) cuando x tiende a un número a es igual a L si los valores de f(x) pueden hacerse arbitrariamente cercanos a L tomando valores de x suficientemente cerca de a. Proporciona dos ejemplos numéricos para ilustrar cómo calcular el límite de una función mediante aproximaciones izquierda y derecha, y confirma los resultados con gráficas.

1. INTRODUCCIÓN: FUNCIONES CONTINUAS Y DISCONTINUAS
FUNCIÓN CONTINUA FUNCIÓN DISCONTINUA
REMOVIBLE
FUNCIÓN DISCONTINUA POR SALTO DISCONTINUIDAD INFINITA

2. Capítulo 2
LÍMITE DE UNA FUNCIÓN
DEFINICIÓN:
Supongamos que 𝑓(𝓍) está definido cuando 𝓍 esta cerca de un numero 𝒶. Entonces se
escribe:
lim
𝓍→𝒶
𝑓(𝓍) = 𝐿
y se dice “ El limite de 𝑓(𝓍), cuando 𝓍 tiende a 𝒶 , es igual a L”, si se puede hacer que
los valores de 𝑓(𝓍) estén arbitrariamente cercanos a L (tan cercanos a L como se pueda),
tomando valores de 𝓍 suficientemente cerca de 𝒶 (por ambos lados de 𝒶), pero no
iguales a 𝒶.
Ejemplo 1: Determine el valor de lim
𝓍→2
𝑥−2
𝑥2−4
Solución:
𝑓(𝑥) =
𝑥−2
𝑥2−4
, 𝑥 ≠ 2 ,-2
La función no esta definida para 𝑥 = 2, para calcular el limite de la función debemos
considerar valores cercanos a 2.

3. APROX. IZQUIERDA APROX. DERECHA
Como las tablas dan una aproximación de 0.25 podemos decir que: lim
𝓍→2
𝑥−2
𝑥2−4
= 0.25
A continuación se muestra la gráfica de la función la cual confirma el resultado del lÍmite.
𝑥 < 2 𝑥 − 2
𝑥2 − 4
1 0.3333
1.5 0.2857
1.9 0.2564
1.99 0.2506
1.999 0.25006
0.25
𝑥 > 2 𝑥 − 2
𝑥2 − 4
3 0.2
2.5 0.2222
2.1 0.2439
2.01 0.2493
2.001 0.2499
0.25

4. Ejemplo 2: Determine el valor de lim
𝓍→−3
𝑥2−9
𝑥+3
Solución:
𝑓(𝑥) =
𝑥2
− 9
𝑥 + 3
, 𝑥 ≠ −3
La función no esta definida para 𝑥 = −3, para calcular el limite de la función debemos
considerar valores cercanos a -3
APROX. IZQUIERDA APROX. DERECHA
𝑥 < −3 𝑓(𝑥) =
𝑥2
− 9
𝑥 + 3
-4 -7
-3.5 -6.5
-3.1 -6.1
-3.01 -6.01
-3.001 -6.001
-3.0001 -6.0001
-6
𝑥 > −3 𝑓(𝑥) =
𝑥2
− 9
𝑥 + 3
-2 -5
-2.5 -5.5
-2.9 -5.9
-2.99 -5.99
-2.999 -5.999
-2.9999 -5.9999
-6

5. Como las tablas dan una aproximación de -6 podemos decir que: lim
𝓍→−3
𝑥2−9
𝑥+3
= −6
A continuación se muestra la gráfica de la función la cual confirma el resultado del lÍmite.