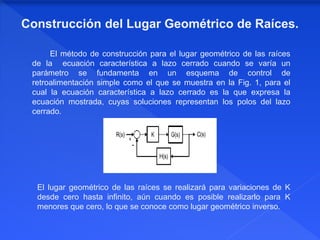
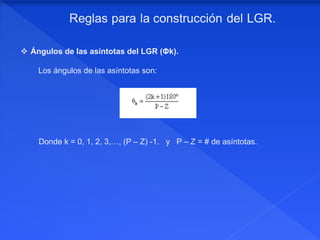
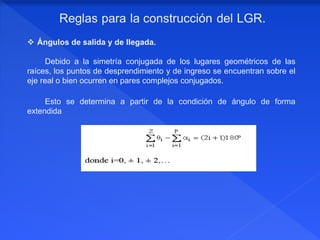
El documento describe el método del lugar geométrico de raíces, el cual grafica las raíces de la ecuación característica de un sistema de control para diferentes valores de un parámetro. Explica las reglas para construir el lugar geométrico, incluyendo dibujar los polos y ceros del sistema abierto, determinar la existencia del lugar geométrico en el eje real, y trazar las asíntotas y puntos de ruptura. El propósito es analizar el comportamiento del sistema de lazo cerrado.