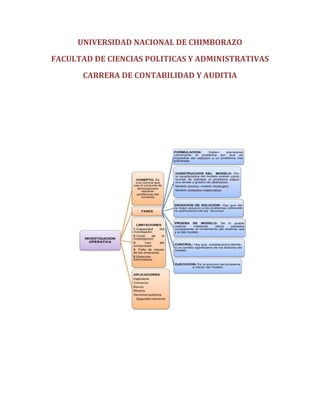
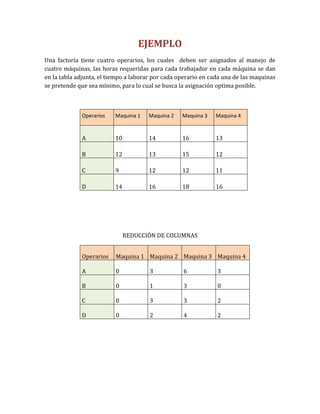
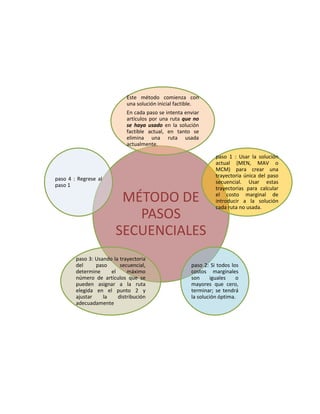
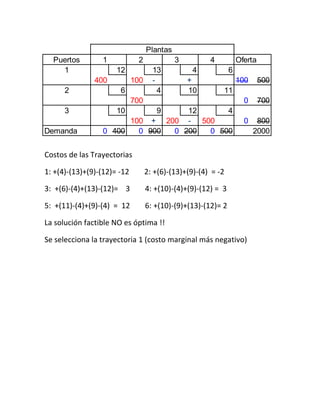
El documento describe diferentes métodos para resolver problemas de transporte y asignación de recursos en programación lineal, como el método de esquina noroeste, el método del costo mínimo, el método de Vogel y el método húngaro. Proporciona ejemplos para ilustrar cada método y explica los pasos involucrados en su aplicación.

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLITICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITIA

2. MODELO DE TRANSPORTE
Existen dos aplicaciones importantes de la programación lineal que son el modelo de transportes y el de asignación de recursos. Aún cuando la solución de estos modelos puede obtenerse aplicando el método simplex, se estudian algoritmos especiales para la solución de estos problemas. Debido a su estructura especial, hace posible hace posible métodos de solución más eficientes en términos del cálculo.

3. MÉTODO DE ESQUINA NOROESTE
Paso 1. Seleccionar la celda de la esquina noroeste (esquina superior izquierda) para un envío.
Paso 2. Hacer el más grande envío como pueda en la celda de la esquina noroeste. Esta operación agotara completamente la disponibilidad de suministros en un origen a los requerimientos de demanda en un destino.
Paso 3. Corregir los números del suministro y requerimientos para reflejar lo que va quedando de suministro y requerimiento y regrese al paso 1.
El método de la esquina es un método de programación lineal hecho a mano para encontrar una solución inicial factible del modelo, muy conocido por ser el método mas fácil al determinar una solución básica

4. EJEMPLO
Valor FO: 400*12+100*13+700*4+100*9+200*12+500*4= $14.200
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 0 400 900 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 100 500
2 6 4 10 11
700 0 700
3 10 9 12 4
100 700 800
Demanda 0 400 0 900 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 100 500
2 6 4 10 11
700 0 700
3 10 9 12 4
100 200 500 0 800
Demanda 0 400 0 900 200 500 2000

5. EL MÉTODO DEL COSTO MÍNIMO
es un algoritmo desarrollado con el objetivo de resolver problemas de transporte o distribucion arrojando mejores resultados que métodos como el de la esquina noroeste, dado que se enfoca en las rutas que presentan menores costos
PASO 1:
De la matriz se elige la ruta y se le asigna la mayor cantidad de unidades posible, cantidad que se ve restringida ya sea por las restricciones de oferta o de demanda
PASO 2:
En este paso se procede a eliminar la fila o destino cuya oferta o demanda sea 0 después del "Paso 1",
PASO 3:
Una vez en este paso existen dos posibilidades, la primera que quede un solo renglón o columna, si este es el caso se ha llegado al final el método, "detenerse".

6. EJEMPLO
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 0 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 200 500 2000

7. Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
500 300 800
Demanda 400 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4
500 300 800
Demanda 400 200 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4 100
200 500 300 800
Demanda 400 200 900 0 200 0 500 2000

8. Valor FO: 300(12)+200(4)+700(4)+100(10)+200(9)+500(4)= 14800
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4 100 0
100 200 500 300 800
Demanda 300 400 200 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6 0
300 200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4 100 0
100 200 500 300 800
Demanda 300 400 200 900 0 200 0 500 2000

9. MÉTODO DE APROXIMACIÓN DE VOGEL
Es un método heurístico de resolución de problmas de transporte capaz de alcanzar una solución básica no artificial de inicio,
PASO 1
Determinar para cada fila y columna una medida de penalización restando los dos costos menores en filas y columnas.
PASO 2
Escoger la fila o columna con la mayor penalización, es decir que de la resta realizada en el "Paso 1" se debe escoger el número mayor
PASO 3
De la fila o columna de mayor penalización determinada en el paso anterior debemos de escoger la celda con el menor costo, y en esta asignar la mayor cantidad posible de unidades.

10. EJEMPLO
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 2
500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 200 500 2000
Penalidades 4 5 6 2
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 0 200 500 2000

11. Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 0 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 6
200 300 500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 0 200 500 2000
Penalidades 4 5 2

12. Costo: 200*4+300*6+700*4+400*10+200*9+200*4 = $12.000
PlantasPuertos1234Oferta1121346200300300500264101170007003109124400200200600800Demanda40090002002005002000

13. MÉTODO HÚNGARO
Este algoritmo se usa para resolver problemas de minimización, ya que es más eficaz que el empleado para resolver el problema del transporte por el alto grado de degeneración que pueden presentar los problemas de asignación.
Paso 1.- Empiece por encontrar el elemento más pequeño en cada renglón de la matriz de costos.
Paso 2.- Dibuje el mínimo número de líneas (horizontales o verticales) que se necesitan para cubrir todos los ceros en la matriz de costos reducidos.
Paso 3.- Encuentre el menor elemento no cero

14. EJEMPLO
Una factoría tiene cuatro operarios, los cuales deben ser asignados al manejo de cuatro máquinas, las horas requeridas para cada trabajador en cada máquina se dan en la tabla adjunta, el tiempo a laborar por cada operario en cada una de las maquinas se pretende que sea mínimo, para lo cual se busca la asignación optima posible.
Operarios Maquina 1 Maquina 2 Maquina 3 Maquina 4 A
10
14
16
13 B
12
13
15
12 C
9
12
12
11 D
14
16
18
16
REDUCCIÓN DE COLUMNAS Operarios Maquina 1 Maquina 2 Maquina 3 Maquina 4 A
0
3
6
3 B
0
1
3
0 C
0
3
3
2 D
0
2
4
2

15. Operarios Maquina 1 Maquina 2 Maquina 3 Maquina 4 A
0
3
3
3 B
0
0
0
0 C
0
2
0
2 D
0
1
1
2
Operarios Maquina 1 Maquina 2 Maquina 3 Maquina 4 A
0
2
3
2 B
1
0
1
0 C
0
1
0
1 D
0
0
1
1
Operarios Maquina 1 Maquina 2 Maquina 3 Maquina 4 A
10
B
12 C
12
D
16
RESPUESTA: 10+12+12+16= 40

16. MÉTODO DE PASOS SECUENCIALES
Este método comienza con una solución inicial factible.
En cada paso se intenta enviar artículos por una ruta que no se haya usado en la solución factible actual, en tanto se elimina una ruta usada actualmente.
paso 1 : Usar la solución actual (MEN, MAV o MCM) para crear una trayectoria única del paso secuencial. Usar estas trayectorias para calcular el costo marginal de introducir a la solución cada ruta no usada.
paso 2: Si todos los costos marginales son iguales o mayores que cero, terminar; se tendrá la solución óptima.
paso 3: Usando la trayectoria del paso secuencial, determine el máximo número de artículos que se pueden asignar a la ruta elegida en el punto 2 y ajustar la distribución adecuadamente
paso 4 : Regrese al paso 1

17. EJEMPLO
Trayectoria 1: +C13-C12+C32-C33
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 100 500
2 6 4 10 11
700 0 700
3 10 9 12 4
100 200 500 0 800
Demanda 0 400 0 900 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 - + 100 500
2 6 4 10 11
700 0 700
3 10 9 12 4
100 + 200 - 500 0 800
Demanda 0 400 0 900 0 200 0 500 2000

18. Costos de las Trayectorias
1: +(4)-(13)+(9)-(12)= -12 2: +(6)-(13)+(9)-(4) = -2
3: +(6)-(4)+(13)-(12)= 3 4: +(10)-(4)+(9)-(12) = 3
5: +(11)-(4)+(9)-(4) = 12 6: +(10)-(9)+(13)-(12)= 2
La solución factible NO es óptima !!
Se selecciona la trayectoria 1 (costo marginal más negativo)
PlantasPuertos1234Oferta1121346400100-+100500264101170007003109124100+200-5000800Demanda04000900020005002000