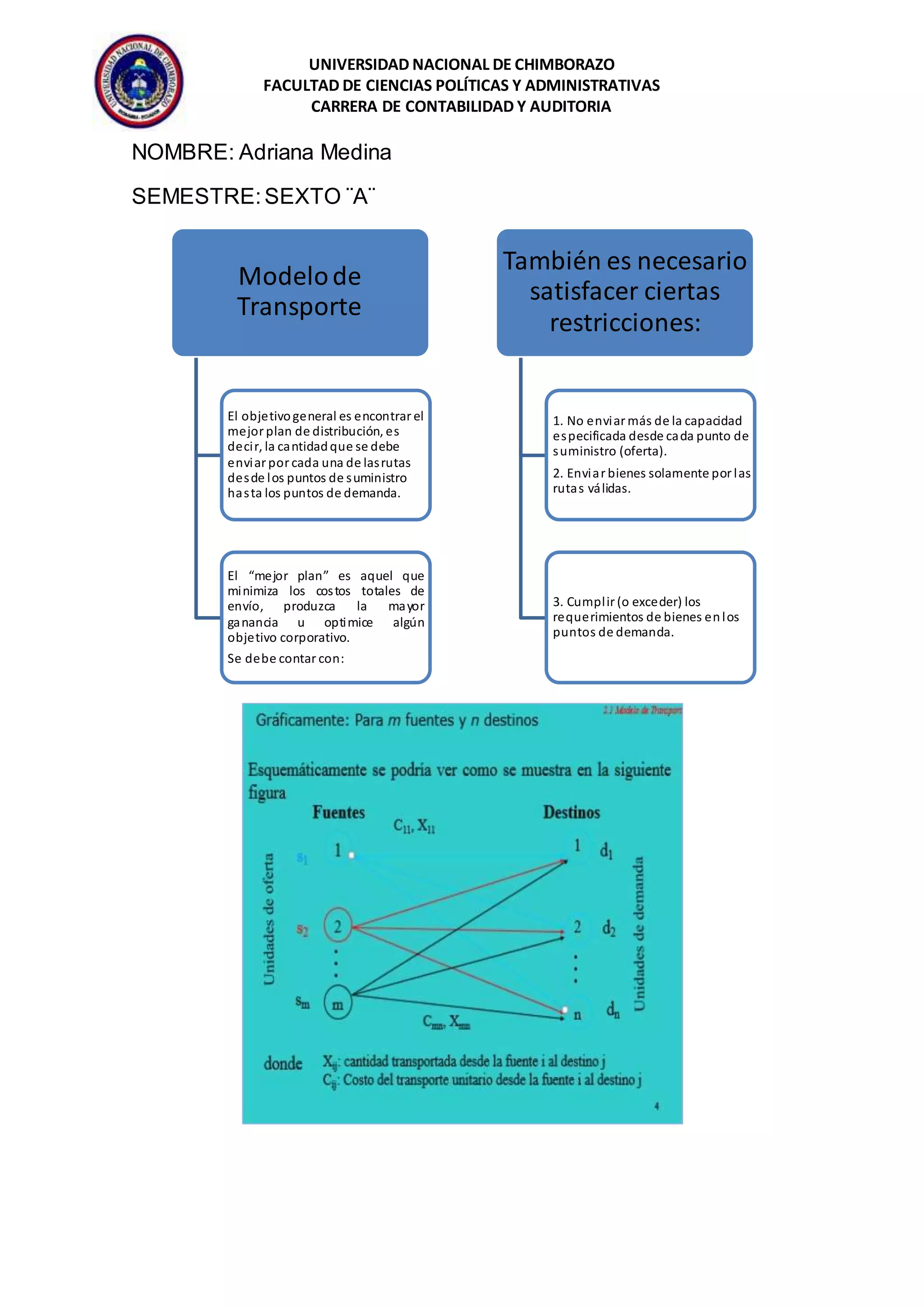
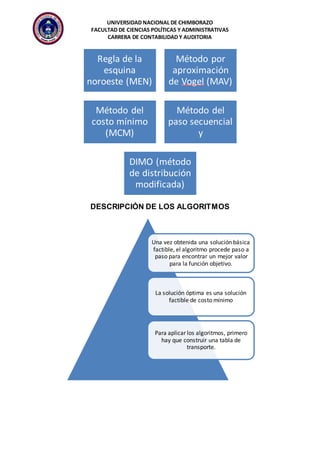
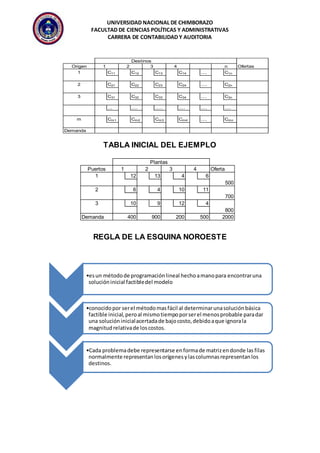
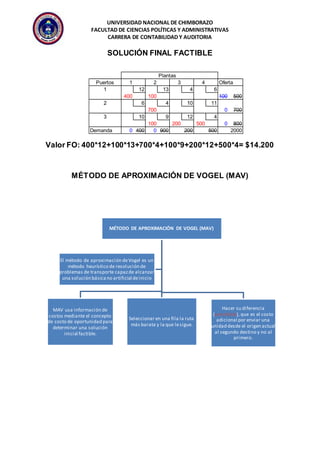
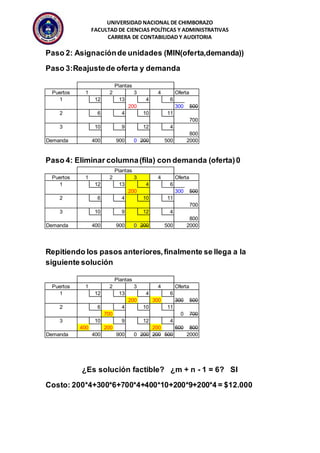
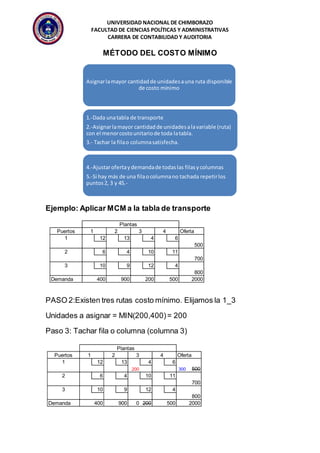
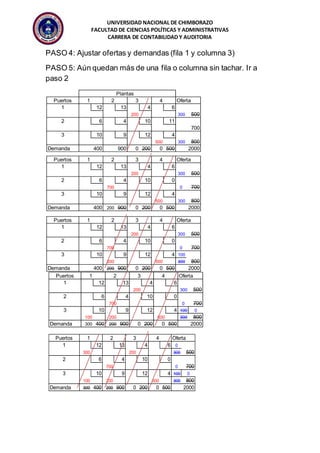
El documento describe diferentes métodos para resolver problemas de transporte, incluyendo la regla de la esquina noroeste, el método de aproximación de Vogel, y el método del costo mínimo. El objetivo es encontrar la distribución óptima de bienes que minimice los costos totales, satisfaga la demanda, y no exceda la oferta, sujeto a restricciones en la capacidad y rutas disponibles.

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
NOMBRE: Adriana Medina
SEMESTRE: SEXTO ¨A¨
Modelo de
Transporte
El objetivo general es encontrar el
mejor plan de distribución, es
deci r, la cantidad que se debe
enviar por cada una de las rutas
desde los puntos de suministro
has ta los puntos de demanda.
El “me jor plan” es aquel que
minimiza los cos tos totales de
envío, produzca la mayor
ganancia u optimice algún
objetivo corporativo.
Se debe contar con:
También es necesario
satisfacer ciertas
restricciones:
1. No enviar más de la capacidad
especificada desde cada punto de
suministro (oferta).
2. Enviar bienes solamente por las
ruta s válidas.
3. Cumpl ir (o exceder) los
requerimientos de bienes en los
puntos de demanda.

2. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
Regla de la
esquina
noroeste (MEN)
Método por
aproximación
de Vogel (MAV)
Método del
costo mínimo
(MCM)
Método del
paso secuencial
y
DIMO (método
de distribución
modificada)
DESCRIPCIÓN DE LOS ALGORITMOS
Una vez obtenida una solución básica
factible, el algoritmo procede paso a
paso para encontrar un mejor valor
para la función objetivo.
La solución óptima es una solución
factible de costo mínimo
Para aplicar los algoritmos, primero
hay que construir una tabla de
transporte.

3. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
Destinos
Origen 1 2 3 4 n Ofertas
1 C11 C12 C13 C14 .... C1n
2 C21 C22 C23 C24 .... C2n
3 C31 C32 C33 C34 .... C3n
... .... ..... .... .... ....
m Cm1 Cm2 Cm3 Cm4 .... Cmn
TABLA INICIAL DEL EJEMPLO
REGLA DE LA ESQUINA NOROESTE
•es un método de programación lineal hecho a mano para encontrar una
solución inicial factible del modelo
•conocido por ser el método mas fácil al determinar una solución básica
factible inicial, pero al mismo tiempo por ser el menos probable para dar
una solución inicial acertada de bajo costo, debido a que ignora la
magnitud relativa de los costos.
•Cada problema debe representarse en forma de matriz en donde las filas
normalmente representan los orígenes y las columnas representan los
destinos.
Demanda
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 200 500 2000

4. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
ALGORITMO DE RESOLUCIÓN
Los pasos para solucionar un problema de programación lineal por
este método son:
2. Hacer el más grande
envío como pueda en la
celda de la esquina
noroeste. Esta operación
agotara completamente la
disponibilidad de
suministros en un origen a
los requerimientos de
demanda en un destino.
PRIMERA ASIGNACIÓN
1. Seleccionar la celda de
la esquina noroeste
(esquina superior
izquierda) para un envío.
HASTA CUARTA ASIGNACIÓN
3. Corregir los números
del suministro y
requerimientos para
reflejar lo que va
quedando de suministro y
requerimiento y regrese al
paso 1.
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 0 400 900 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 100 500
2 6 4 10 11
700 0 700
3 10 9 12 4
100 700 800
Demanda 0 400 0 900 200 500 2000

5. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
SOLUCIÓN FINAL FACTIBLE
Valor FO: 400*12+100*13+700*4+100*9+200*12+500*4= $14.200
MÉTODO DE APROXIMACIÓN DE VOGEL (MAV)
MÉTODO DE APROXIMACIÓN DE VOGEL (MAV)
MAV usa información de
costos mediante el concepto
de costo de oportunidad para
determinar una solución
inicial factible.
Seleccionar en una fila la ruta
más barata y la que le sigue.
Hacer su diferencia
(penalidad), que es el costo
adicional por enviar una
unidad desde el origen actual
al segundo destino y no al
primero.
El método de aproximación de Vogel es un
método heurístico de resolución de
problemas de transporte capaz de alcanzar
una solución básica no artificial de inicio
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
400 100 100 500
2 6 4 10 11
700 0 700
3 10 9 12 4
100 200 500 0 800
Demanda 0 400 0 900 200 500 2000

6. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
1. Identificar la fila o
columna con la máxima
penalidad.
5. Calcular los nuevos
costos de penalidad.
Paso 0: Cálculo de penalidades
2.Colocar la máxima
asignación posible a la
ruta no usada que tenga
menor costo en la fila o
columna seleccionada en
el punto 1 (los empates
se resuelven
arbitrariamente)
3. Reajustar la oferta y
demanda en vista de
esta asignación.
4. Eliminar la columna en
la que haya quedado una
demanda 0 (o la fila con
oferta 0), de
consideraciones
posteriores.
Plantas
Puertos 1 2 3 4 Oferta Penalidades
1 12 13 4 6 2
500
2 6 4 10 11 2
700
3 10 9 12 4 5
800
Demanda 400 900 200 500 2000
Penalidades 4 5 6 2

7. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
Paso 2: Asignación de unidades (MIN(oferta,demanda))
Paso 3:Reajuste de oferta y demanda
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 0 200 500 2000
Paso 4: Eliminar columna (fila) con demanda (oferta) 0
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 0 200 500 2000
Repitiendo los pasos anteriores, finalmente se llega a la
siguiente solución
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 300 500
2 6 4 10 11
700 0 700
3 10 9 12 4
400 200 200 600 800
Demanda 400 900 0 200 200 500 2000
¿Es solución factible? ¿m + n - 1 = 6? SI
Costo: 200*4+300*6+700*4+400*10+200*9+200*4 = $12.000

8. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
MÉTODO DEL COSTO MÍNIMO
Asignar la mayor cantidad de unidades a una ruta disponible
de costo mínimo
1.-Dada una tabla de transporte
2.-Asignar la mayor cantidad de unidades a la variable (ruta)
con el menor costo unitario de toda la tabla.
3.- Tachar la fila o columna satisfecha.
4.-Ajustar oferta y demanda de todas las filas y columnas
5.-Si hay más de una fila o columna no tachada repetir los
puntos 2, 3 y 45.-
Ejemplo: Aplicar MCM a la tabla de transporte
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
PASO 2:Existen tres rutas costo mínimo. Elijamos la 1_3
Unidades a asignar = MIN(200,400) = 200
Paso 3: Tachar fila o columna (columna 3)
500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 200 500 2000
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
800
Demanda 400 900 0 200 500 2000

9. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORIA
PASO 4: Ajustar ofertas y demandas (fila 1 y columna 3)
PASO 5: Aún quedan más de una fila o columna sin tachar. Ir a
paso 2
Plantas
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 11
700
3 10 9 12 4
500 300 800
Demanda 400 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4
500 300 800
Demanda 400 200 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4 100
200 500 300 800
Demanda 400 200 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6
200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4 100 0
100 200 500 300 800
Demanda 300 400 200 900 0 200 0 500 2000
Puertos 1 2 3 4 Oferta
1 12 13 4 6 0
300 200 300 500
2 6 4 10 0
700 0 700
3 10 9 12 4 100 0
100 200 500 300 800
Demanda 300 400 200 900 0 200 0 500 2000