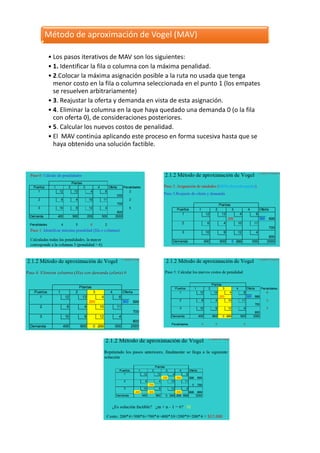
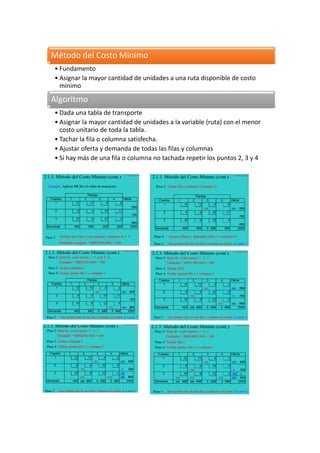
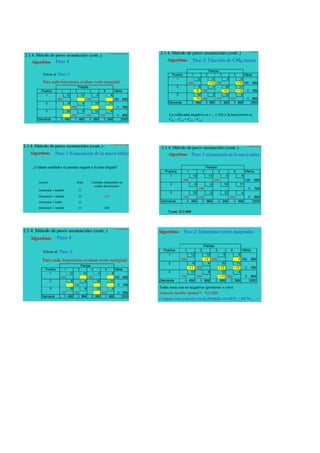
Este documento describe métodos para resolver problemas de programación lineal como el modelo de transporte. El objetivo general es encontrar el plan de distribución óptimo que minimice los costos totales. Se requiere conocer la oferta, demanda y costos de transporte. Los métodos descritos incluyen la regla de la esquina noroeste, el método de Vogel y el método del costo mínimo para encontrar una solución inicial factible, y el método del escalón y DIMO para encontrar la solución óptima.

1. PROGRAMACIÓN LINEAL APLICACIONES
Solución del Modelo de Transporte
objetivo general Es encontrar el mejor plan de distribución,
El “mejor plan” es aquel que minimiza los costos totales de envío, produzca la mayor ganancia u optimice algún objetivo corporativo.
Se debe contar con: Nivel de oferta en cada fuente y la cantidad de demanda en cada destino.
Costo de transporte unitario de mercadería desde cada fuente a cada destino.

2. Descripción de los algoritmos
La regla de la esquina noroeste, el método de aproximación de Vogel y el método del costo mínimo son alternativas para encontrar una solución inicial factible.
El método del escalón y el DIMO son alternativas para proceder de una solución inicial factible a la óptima.
Por tanto, el primer paso es encontrar una solución inicial factible, que por definición es cualquier distribución de ofertas que satisfaga todas las demandas
Para aplicar los algoritmos, primero hay que construir una tabla de transporte.
La solución óptima es una solución factible de costo mínimo
Una vez obtenida una solución básica factible, el algoritmo procede paso a paso para encontrar un mejor valor para la función objetivo.

3. MÉTODO ESQUINA DE NOROESTE
•Regla de la esquina Noroeste
•Se inicia el proceso desde la esquina izquierda superior
•Se ubican tantas unidades como sea posible en la ruta
•Cantidad de Unidades = Mínimo(disponibilidad, demanda)
•Las siguientes asignaciones se hacen o bien recorriendo hacia la derecha o bien hacia abajo.
•Las demandas se satisfacen recorriendo sucesivamente de izquierda a derecha y las ofertas se destinan recorriendo de arriba hacia abajo.

4. Método de aproximación de Vogel (MAV)
•Los pasos iterativos de MAV son los siguientes:
•1. Identificar la fila o columna con la máxima penalidad.
•2.Colocar la máxima asignación posible a la ruta no usada que tenga menor costo en la fila o columna seleccionada en el punto 1 (los empates se resuelven arbitrariamente)
•3. Reajustar la oferta y demanda en vista de esta asignación.
•4. Eliminar la columna en la que haya quedado una demanda 0 (o la fila con oferta 0), de consideraciones posteriores.
•5. Calcular los nuevos costos de penalidad.
•El MAV continúa aplicando este proceso en forma sucesiva hasta que se haya obtenido una solución factible.

5. Método del Costo Mínimo
•Fundamento
•Asignar la mayor cantidad de unidades a una ruta disponible de costo mínimo
Algoritmo
•Dada una tabla de transporte
•Asignar la mayor cantidad de unidades a la variable (ruta) con el menor costo unitario de toda la tabla.
•Tachar la fila o columna satisfecha.
•Ajustar oferta y demanda de todas las filas y columnas
•Si hay más de una fila o columna no tachada repetir los puntos 2, 3 y 4