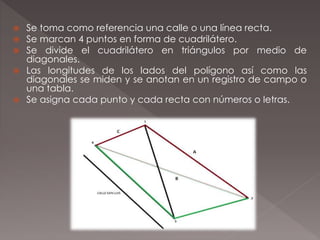
El método de diagonales consiste en dividir un polígono en triángulos trazando diagonales entre sus vértices. Se miden las longitudes de los lados del polígono y las diagonales, anotándolas. Los triángulos formados deben cumplir que la suma de sus ángulos sea 180 grados, aunque inevitablemente haya pequeños errores. El método implica medir un cuadrilátero de referencia trazando sus diagonales para dividirlo en triángulos, registrar las mediciones y asignar números o letras a cada punto y recta.

2.  Consiste en dividir en triángulos, el polígono base por
medio de las diagonales. Las longitudes de los lados del
polígono y de las diagonales se miden, anotándose en el
registro de campo. No necesariamente han de ser
triángulos las figuras formadas; también pueden ser
cuadriláteros (con una o dos diagonales) o cualquier otro
polígono que permita su descomposición en triángulos.
 Los ángulos de cada triangulo deben sumar 180º; debido
a pequeños errores inevitables, esto no se logra
exactamente y , así, se presenta un pequeño error en
cada triangulo (cierre en ángulo). De acuerdo con el
grado de precisión deseada, este error tiene un valor
máximo tolerable. También se puede encontrar el error
de cierre en lado de la base, o sea, la diferencia que se
encuentra entre la base calculada, una vez ajustados los
ángulos, y la base medida, expresada unitariamente.

3.  Se toma como referencia una calle o una línea recta.
 Se marcan 4 puntos en forma de cuadrilátero.
 Se divide el cuadrilátero en triángulos por medio de
diagonales.
 Las longitudes de los lados del polígono así como las
diagonales se miden y se anotan en un registro de campo o
una tabla.
 Se asigna cada punto y cada recta con números o letras.

4. EST. P. MEDIDA
1 2 43.18
2 3 28.43
3 4 34.10
4 1 23.67
1 3 36.94
2 4 53.12

7.  En el método de diagonales observamos
que es un método muy sencillo y
practico que al igual que se puede
realizar con cinta lo podemos realizar
con teodolito, requiere que no se
encuentren elementos que obstruyan las
diagonales a marcar, puede haber
ciertos errores con la cinta pero con el
teodolito es mas preciso.