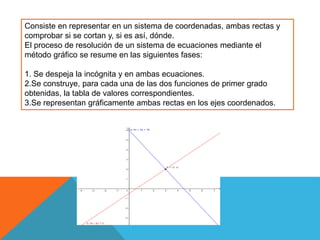
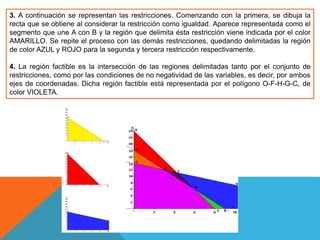
Este documento describe el método gráfico para resolver problemas de programación lineal. Explica que este método involucra representar gráficamente las restricciones y función objetivo en un sistema de coordenadas, y que la solución óptima es el punto que maximice la función objetivo dentro de la región factible definida por las restricciones. También presenta un ejemplo completo de cómo aplicar este método para resolver un problema de tres restricciones y dos variables.

1. Realizado por:
Fabiola Laguna
27.135.024
Ing. De sistemas

2. MÉTODOS DE PROGRAMACIÓN NO
LINEAL
Es el proceso de resolución de un sistema de igualdades y desigualdades
sujetas a un conjunto de restricciones sobre un conjunto de variables
reales desconocidas, con una función objetivo a maximizar, cuando alguna
de las restricciones o la función objetivo no son lineales.
Para llegar a la solución de un problema de Programación Lineal se utilizan
diferentes métodos de solución. Los más difundidos son: el método gráfico
y el Método Simplex. La solución de un problema de Programación Lineal
utilizando un procedimiento gráfico es posible si se tienen no más de dos
variables

3. Consiste en representar en un sistema de coordenadas, ambas rectas y
comprobar si se cortan y, si es así, dónde.
El proceso de resolución de un sistema de ecuaciones mediante el
método gráfico se resume en las siguientes fases:
1. Se despeja la incógnita y en ambas ecuaciones.
2.Se construye, para cada una de las dos funciones de primer grado
obtenidas, la tabla de valores correspondientes.
3.Se representan gráficamente ambas rectas en los ejes coordenados.

4. CARACTERÍSTICAS
• El método gráfico es una forma fácil y rápida para la solución de problemas de
Programación Lineal, siempre y cuando el modelo conste de dos variables.
• Consiste en representar geométricamente las restricciones, condiciones
técnicas y función objetivo.
• Este método se encuentra limitado a problemas de dos o tres variables de
decisión ya que no es posible ilustrar gráficamente más de 3 dimensiones.
Ventajas y desventajas del método gráfico
Ventajas:
-Nos permite realizar un estudio de
todos los puntos de interés de las
funciones.
-Nos permite observar el
comportamiento de las expresiones
que estamos utilizando.
-Podemos observar crecimiento y
decrecimiento de la misma.
Desventajas:
-Puede estar sometido a errores de
escala de la gráfica.
-En ocasiones las gráficas de las
funciones no son sencillas de realizar.
-Podemos cometer errores de
aproximación al momento de observar

5. EJEMPLO:
Maximizar Z = f(x,y) = 3x + 2y
sujeto a: 2x + y ≤ 18
2x + 3y ≤ 42
3x + y ≤ 24
x ≥ 0 , y ≥ 0
Resolver mediante el método Gráfico el siguiente problema:
1. Inicialmente se dibuja el sistema de coordenadas asociando a un eje la
variable "x" y al otro la "y" (generalmente se asocia 'x' al eje horizontal e 'y' al
vertical), como se puede ver en la figura.
2. Se marca en dichos ejes una escala numérica apropiada a los valores que
pueden tomar las variables de acuerdo a las restricciones del problema. Para ello
en cada restricción se hacen nulas todas las variables excepto la correspondiente
a un eje concreto, determinándose así el valor adecuado para dicho eje. Este
proceso se repite para cada uno de los ejes.

6. 3. A continuación se representan las restricciones. Comenzando con la primera, se dibuja la
recta que se obtiene al considerar la restricción como igualdad. Aparece representada como el
segmento que une A con B y la región que delimita ésta restricción viene indicada por el color
AMARILLO. Se repite el proceso con las demás restricciones, quedando delimitadas la región
de color AZUL y ROJO para la segunda y tercera restricción respectivamente.
4. La región factible es la intersección de las regiones delimitadas tanto por el conjunto de
restricciones, como por las condiciones de no negatividad de las variables, es decir, por ambos
ejes de coordenadas. Dicha región factible está representada por el polígono O-F-H-G-C, de
color VIOLETA.

7. Punto extremo Coordenadas (x,y) Valor objetivo (Z )
O (0,0) 0
C (0,14) 28
G (3,12) 33
H (6,6) 30
F (8,0) 24
5. Como existe una región factible, se procede a determinar sus puntos extremos,
o vértices del polígono que representa. Estos vértices son los puntos candidatos a
soluciones óptimas. En este ejemplo son los puntos O-F-H-G-C de la figura.
6. Finalmente, se evalúa la función objetivo (3x + 2y) en cada uno de esos puntos
(resultado que se recoge en la tabla siguiente). Como el punto G proporciona el
mayor valor a la función Z y el objetivo es maximizar, tal punto constituye la
solución óptima: Z = 33 con x = 3 e y = 12.