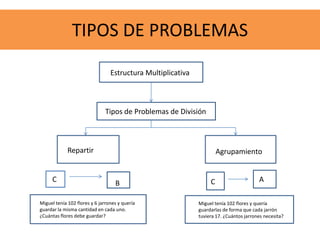
El documento presenta información sobre el desarrollo del pensamiento multiplicativo en los estudiantes. Explica que este pensamiento requiere coordinar la multiplicación y la división. Describe diferentes tipos de problemas multiplicativos como repartir, agrupar, factor multiplicante, razón y producto cartesiano. También proporciona ejemplos de cómo ayudar a los estudiantes a construir un pensamiento multiplicativo simple a través de ejercicios de empacar objetos y situaciones de compra y venta.

1. El pensamiento multiplicativo simple
Taller de inicio
Patricia Jiménez D
acuarimantima4@gmail.com

2. DESPERTAR EL GUSTO POR EL
PENSAMIENTO INDEPENDIENTE
… un profesor de matemáticas tiene una gran oportunidad. Si dedica su tiempo a
ejercitar a los alumnos en operaciones rutinarias, matará en ellos el interés, impedirá su
desarrollo intelectual y acabará desaprovechando su oportunidad. Pero si, por el
contrario, pone a prueba la curiosidad de sus alumnos planteándoles problemas
adecuados a sus conocimientos, y les ayuda a resolverlos por medio de preguntas
estimulantes, podrá despertarles el gusto por el pensamiento independiente y
proporcionarles ciertos recursos para ello.
(George Polya, prefacio a la primera edición en inglés de How to solve it. Princeton
University Press. 1945)

3. ¿Cómo ayudan las docentes a
desarrollar el pensamiento
multiplicativo?
¿Ha escuchado decir a sus
estudiantes:
¿“Para resolver este problema
tengo que multiplicar o dividir”?

4. El pensamiento multiplicativo
El desarrollo del pensamiento multiplicativo exige la coordinación
de la multiplicación y la división. Esta coordinación debe hacerse
en el plano de la acción y el pensamiento.

5. TIPOS DE PROBLEMAS
Estructura Multiplicativa
Tipos de Problemas de División
Repartir Agrupamiento
C B C A
Miguel tenía 102 flores y 6 jarrones y quería Miguel tenía 102 flores y quería
guardar la misma cantidad en cada uno. guardarlas de forma que cada jarrón
¿Cuántas flores debe guardar? tuviera 17. ¿Cuántos jarrones necesita?

6. TIPOS DE PROBLEMAS
Estructura Multiplicativa
Tipos de Problemas de Multiplicación
Factor Razón Producto
multiplicante cartesiano
XB /B A X
A C A C
B
Miguel tiene 17 clases de flores en
El jarrón de Miguel tenía 17 flores, el 6 jarrones tenían 17 flores cada uno.
6 colores diferentes. ¿Cuántas
de Santi 6 veces más. ¿Cuántas flores ¿Cuántas flores hay en todos los
flores diferentes puede obsequiar?
tenía Santi? jarrones?

7. El pensamiento multiplicativo simple
Estructura de algunos problemas
• Un problema es multiplicativo simple cuando puede ser
resuelto mediante una y solo una de las operaciones de
multiplicación y división:
• El problema directo y los dos inversos

8. ¿Cómo ayudar los niños/as a construir un pensamiento
multiplicativo simple?
 -Construir ejemplos en los que los niños/as
tengan que empacar objetos en
cajas, bolsas, o cualquier tipo de empaque.
Varíen la cantidad de objetos que van en
cada unidad de empaque.
 -Buscar que los niños/as se enfrenten a los
tres tipos de problemas multiplicativos
simples.
 -Presentar situaciones que den lugar a
residuos.
 -Idear situaciones en que los niños tengan
que comprar y vender varias unidades de
un mismo artículo, se pueden hacer
recibos parecidos a los reales.

9. El minicomputador de Jorge Castaño: adaptación de la
propuesta original de Papy
Una herramienta para desarrollar el pensamiento matemático practicando la composición y descomposición
Es una herramienta útil para ayudar
a los niños a desarrollar su
pensamiento multiplicativo, se usa
para practicar la composición y
descomposición s utilizando el
esquema multiplicativo y aditivo de
los números. Es fácil de construir. En
cartón o madera se hace un cuadro
como el de la figura.
Se pueden utilizar los colores de las
regletas (base binaria) u otros
colores.
Al colocar un objeto en uno de los
cuadros el objeto representa el valor
del cuadro. Por ejemplo una ficha en
el cuadro marrón representa 8. Si se
colocan varias fichas en el cuadro, se
suman los valores que representan
cada una.
Por ejemplo 8+8+4+2+1+1= 24

10. Lo podemos imprimir
8 4
2 1

11. Práctica colegio de los maristas

12. Minicomputador de Papy-ábaco
m
Unidades
Centenas Decenas

13. El minicomputador de Papy
Descripción general de la experiencia de aula
• Objetivos que se cumplen con el minicomputador:
• 1. Ejercitar el sistema de agrupaciones y pasar a unidades de orden
superior.
• 2. Automatizar el paso de una base a otra.
• 3. Pasar de una base al sistema decimal, realizando agrupación-
transformación (que implica dividir) y el camino inverso-
descomposición (que implica multiplicar).
• 4. Facilitar la comprensión de como se forman los números enteros.
• 5. Agilizar y automatizar el cálculo.
• 6. Acostumbrar a los niños a operar de derecha a izquierda y a leer
los números de izquierda a derecha.

14. RECICLAR TAPAS
JUGAR “CONCENTRESE”
http://aprendiendomatematicas.com/

15. Instrucciones
1. Colocar los factores
2. Simplificar el resultado cambiando
Unidades de primer orden: azul unidades por decenas, etc.
Unidades de segundo orden:
verde
Unidades de tercer orden: rojo

16. OTRA POSIBILIDAD

17. Caja Mackinder
• La caja de Mackinder es un
instrumento que consiste
en diez receptáculos
menores que se
encuentran alrededor de
uno mayor, dispuestos en
una base plana. Los
receptáculos menores
poseen elementos que
representan cantidades
unitarias, las cuales se van
depositando en el
receptáculo mayor
haciendo referencia que la
multiplicación es la suma
progresiva de esos
elementos, y a la inversa
con la división.

18. Materiales para confeccionar una caja Mackínder
10 cajas pequeñas
1 caja grande
Semillas, botones, fichas
o cualquier objeto que se
pueda contar.
Cada caja representará
los grupos formados
http://www.youtube.com/watch?v=7yBToVX4Mjg

19. Estructura aditiva
Suma-adición
Por ejemplo: Podemos presentar esta situación a los(as) niños(as):
Juan compró 6 dulces en la tienda y cuando llegó a casa su mamá le había
traído de regalo 5 dulces. ¿Cuántos dulces reunió Juan?
En un receptáculo se introducen 6 fichas y en otro 5 fichas (que
representan la cantidad de dulces). A continuación se reúnen las fichas en
receptáculo central, (en éste siempre vamos a contener la totalidad, el
todo) y los niños hacen el conteo, sacando las fichas de una en una.
www.rmm.cl/usuarios/.../201010011658510.caja%20Mackinder.doc

20. Estructura aditiva
resta-sustracción
Juan tiene 11 dulces, le regala a su hermanito 5 de sus dulces. ¿Con cuántos
dulces quedó Juan?
Se depositan 11 fichas en el receptáculo central, luego se retiran 5 fichas de
éste y se llevan a uno de los receptáculos laterales. A continuación los
niños/as hacen el conteo de las fichas que quedaron en el receptáculo
central

21. Estructura multiplicativa
División
Juan quiere repartir 9 galletas entre sus tres amigos de tal manera que a cada uno
le corresponda la misma cantidad. ¿Cuántas galletas le corresponde a cada amigo?
Se depositan 8 fichas en el receptáculo central, luego, se seleccionan tres
receptáculos laterales (los tres amigos) y a cada uno se le va depositando de a una
ficha, hasta que la cantidad de fichas del receptáculo central sea menor que la
cantidad de receptáculos elegidos.

22. Estructura multiplicativa
Multiplicación
La tía de Juan está organizando una fiesta el salón comunal con ayuda de Juan . En el
salón hay tres mesas, la tía le pide que coloque tres gaseosas en cada mesa. ¿Cuántas
gaseosas debe alistar Juan?
Se seleccionan tres receptáculos laterales y en cada uno se colocan tres fichas, a
continuación, los niños reúnen todas las fichas en el receptáculo central y las cuentan.

23. Tarjetas de situaciones
Hay 7 niños jugando a la Hay 6 hormigas en una David tiene 8 bolitas.
pelota. Vienen 2 más a piedra. Llegan 3 más. Compra 3 más. ¿Cuántas
jugar. ¿Cuántos niños hay ¿Cuántos insectos hay bolitas tiene ahora?
jugando? sobre la piedra?
Hoy Laura dio 7 saltos en Hay 8 mesas y cada una Hay 8 mesas y cada una
la cuerda. Luego salta 4 debe tener 2 bebidas. debe tener 5 servilletas.
veces más. ¿Cuántos saltos ¿Cuántas bebidas se ¿Cuántas servilletas se
da en total? necesitan? necesitan?
En cada mesa se sentarán Si son 8 mesas y En cada mesa se sentarán
5 niños/as. Si a cada niño/a necesitamos 10 galletas 5 niños/as. Si a cada niño/a
le daremos 5 colombinas, para cada una, ¿cuántas le daremos 3 panes,
¿cuántos colombinas galletas necesitamos en ¿cuántos panes
necesitamos por mesa? total? necesitamos por mesa?

24. Tarjetas de situaciones
Hay 7 niños jugando a la Hay 14 hormigas en una Carlos tiene 8 canicas y
pelota, si se van 2. piedra y 5 de ellas se van a jugando perdió 2.
¿Cuántos niños quedan una hoja cercana. ¿Cuántas canicas tiene
jugando? ¿Cuántas hormigas ahora?
quedaron sobre la piedra?
Si Lina tiene 11 panes y Hay 9 mesas y 18 Si se tiene una bolsa de 20
regalas 5 de ellos. gaseosas. Si queremos dulces. Hay 10 mesas y
¿Cuántos panes le repartir la misma cantidad cada una debe tener la
quedaron? de gaseosas por mesa, misma cantidad de dulces.
¿cuántas gaseosas deben ¿Cuántos dulces se deben
haber en cada mesa? colocar en cada mesa?
Si en un curso hay 40 niños Si vamos a distribuir 20 En cada mesa se colocaron
y queremos organizar canicas en 5 bolsas, de tal 30 panes. Si hay 6 niños/as
grupos de a 5 niños por manera que queden la por mesa y cada uno debe
mesa. ¿Cuántas mesas misma cantidad en cada tomar la misma cantidad
necesitamos? bolsa. ¿Cuántas canicas de panes. ¿Cuántos panes
debe tener cada bolsa? debe tomar cada niño/a?

25. Actividad con la caja mackinder
Para cualquier estructura que usted esté enseñando a los niños/as, puede
organizar el juego de la siguiente manera:
1. Distribuya en grupos a los niños/as.
2. A cada grupo de niños/as entregue una caja mackinder.
3. Coloque al lado del receptáculo central las tarjetas de situaciones.
4. Proponga a los niños/as un criterio para ordenar los turnos.
5. El niño/a a quien le correspondió el primer turno, toma una tarjeta de
situación y la resuelve empleando la caja mackinder, los demás niños
deben estar atentos por si acaso éste comete un error y deben ayudarlo.
6. Una vez termine, continua el niño/a a quien le corresponde el siguiente
turno.

26. bibliografía
• CASTAÑO, Jorge. (1.995-1998). Hojas pedagógicas 1 al 10.
Colección: Matemática Serie lo numérico. Proyecto: Descubro
la Matemática. Fundación Restrepo Barco.
• GRISALES, A. OROZCO, J. (2010). Juega y Construye la
Matemática. Aportes y reflexiones. Colegios Maristas.
Provincia Norandina – Colombia. Material fotocopiado. 150 p.
• FERNANDEZ, Josefa y RODRÍGUEZ María. (1997). Juegos y
pasatiempos en la enseñanza de la matemática elemental.
Editorial Síntesis. Madrid.
• Dickson. El aprendizaje de las matemáticas. Edit labor.

27. POR LA ATENCIÓN Y DISPOSICIÓN