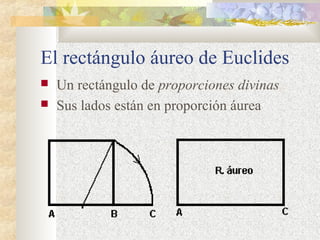
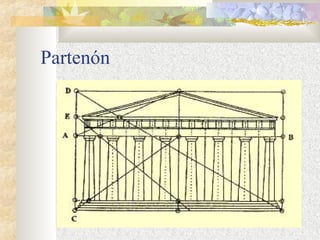
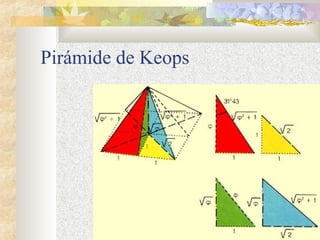
El documento habla sobre la proporción áurea o número de oro, que es una proporción matemática que se encuentra en la naturaleza y que los artistas han utilizado desde la antigüedad para crear formas bellas. Los griegos desarrollaron esta proporción en una fórmula matemática y la usaron en obras maestras como el Partenón. Más tarde, artistas como Leonardo da Vinci y Salvador Dalí también se basaron en esta proporción en sus obras.

1. Número de oro

2. Proporciones
 Desde la antigüedad,
los artistas se
ocuparon de encontrar
una razón que
produjera una forma
ideal para representar
la belleza en las
figuras y en la
arquitectura.

3. Esa razón es la proporción ideal entre los
elementos que integran la obra artística.
Los artistas la utilizan desde la más remota
antigüedad.
Los griegos la desarrollaron en fórmula
matemática.
No fue regla arbitraria establecida al azar,
sino fruto de un constante estudio de la
naturaleza.

4. Vieron que en la naturaleza, y en la misma
figura humana, se daba esta proporción de
líneas constante.
Pensaron que era obra de Dios al dar el ser a
sus criaturas.

5. Se conoce ya de su existencia en
los pentágonos regulares y
pentáculos de las tabletas
sumerias de alrededor del
3200 a. C.

6. Proporción divina
Dividimos un segmento cualquiera en dos
partes, a y b , de manera que la razón
entre la totalidad del segmento y la parte a
sea igual a la razón entre la parte a y la
parte b.

7. Expresado matemáticamente:

8. Para los de matemáticas:

9. Número de oro
 Su valor es de 1,61803 ...
 Se le representa con una letra griega: Φ
En honor a Fidias, escultor griego

10. El rectángulo áureo de Euclides
 Un rectángulo de proporciones divinas
 Sus lados están en proporción áurea

11. Fidias, autor del Partenón

12. Partenón

13. Leonardo usó el número Φ
 Εl cociente entre el
lado del cuadrado y
el radio de la
circunferencia que
tiene por centro el
ombligo, es el
número de oro

14. El pentáculo
Existe la relación del
número áureo también en
el pentáculo, un símbolo
pagano, más tarde
acogido por la iglesia
católica para representar
a la Virgen María.

15. En el cuerpo humano
La comprobación empírica de los
humanistas en el siglo XV determinó
que existía una relación: Φ, si se dividia
el resultado de medir, desde el hombro
hasta la punta de los dedos de la mano
extendida, por el resultado de la medida
desde el codo hasta la punta extendida
de los dedos.

16.  Lo mismo ocurría dividiendo la
medidas desde la cadera al suelo
entre la medida desde la rodilla al
suelo.
 O también existía la proporción Φ al
dividir la altura total por la medida
resultante desde el ombligo al suelo.

17. En el arte
Existen relaciones
basadas en la
sección áurea en
algunas de las más
célebres estatuas
griegas como el
Hermes de
Praxíteles (390-
330 a. C.).

18. Aparece en la
Venus de Milo

19. El cuadro de Dalí Leda atómica, pintado en
1949, sintetiza siglos de tradición
matemática y simbólica, especialmente
pitagórica.
Se trata de una filigrana basada en la
proporción áurea, pero elaborada de tal
forma que no es evidente para el
espectador.
En el boceto de 1947 se advierte la
meticulosidad del análisis geométrico
realizado por Dalí basado en el pentagrama
místico pitagórico.

20. Leda
atómica,
Salvador
Dalí, 1949

21. Pirámide de Keops, 2570 a.C

22. Pirámide de Keops

23. En la
naturaleza

24. El Nautilus

25. En la música
 En varias sonatas para piano de Mozart, la
proporción entre el desarrollo del tema y su
introducción es la más cercana posible a la
razón áurea. ¿Intuición?
 Tampoco se sabe si fue consciente de ello,
pero en su Quinta Sinfonía Beethoven
distribuye el famoso tema siguiendo la
sección áurea.

26. En la música
 Autores como Bártok, Messiaen y
Stockhausen, entre otros, compusieron
obras cuyas unidades formales se
relacionan (a propósito) con la sección
áurea.

27. A ti, maravillosa disciplina,
media, extrema razón de la hermosura,
que claramente acata la clausura
viva en la malla de tu ley divina.
A ti, cárcel feliz de la retina,
áurea sección, celeste cuadratura,
misteriosa fontana de mesura
que el Universo armónico origina.
A ti, mar de los sueños, angulares,
flor de las cinco formas regulares,
dodecaedro azul, arco sonoro.
Luces por alas un compás ardiente.
Tu canto es una esfera transparente.
A ti, divina proporción de oro.
Rafael Alberti