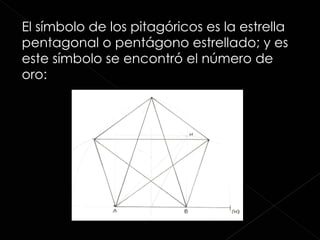
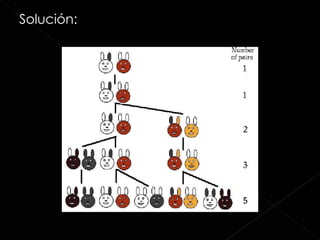
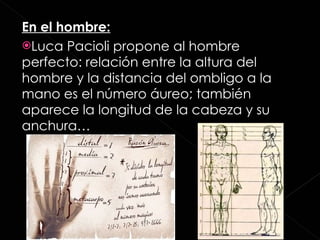
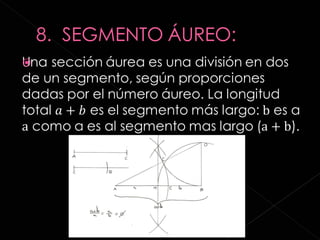
Este documento define la proporción áurea y explica sus diferentes nombres, símbolos y descubridores a lo largo de la historia. También describe cómo la proporción áurea se encuentra en la naturaleza y el arte, incluyendo la arquitectura, música y el cuerpo humano. Finalmente, proporciona varias fuentes para obtener más información sobre este tema.

1. Houssam Akeb Daoud Jacobo Fiaño Salinas

2. DEFINICIÓN: RAZÓN Y PROPORCIÓN ¿DE CUÁNTAS MANERAS SE LE LLAMA A LA PROPORCIÓN ÁUREA, CON QUÉ SIGNO SE LA DENOMIDA? PERSONAJES RELEVANTES A LOS LARGO DE LA HISTORIA QUE HAN HECHO IMPORTANTES DESCUBRIMIENTOS EN LA PROPORCIÓN ÁUREA EL SÍMBOLO PITAGÓRICO SUCESIÓN DE FIBONACCI ORÍGENES DE LA PROPORCIÓN AÚREA Y SUS APLICACIONES EN LA ARQUITECTURA Y EN EL ARTE SEGMENTO ÁUREO RELACIÓN DE LA PROPORCIÓN ÁUREA Y LA NATURALEZA EL CÓDIGO DE LA PROPORCIÓN ÁUREA FUENTES

3. La razón geométrica es la comparación de dos cantidades por su cociente; supone la cantidad de determinar cuántas veces contiene la una a la otra. La razón entre dos números a y b se expresa así: a : b , a / b . Donde a a se le llama antecedente y a b consecuente; y ambos son los términos de la razón.

4. Las proporciones geométricas son las más utilizadas, se aplican al estudio de las figuras semejantes .

5. El ‘‘ número áureo ’’ o ‘‘ número de oro ’’ también es llamado número plateado , razón extrema y media , razón áurea , media áurea , proporción áurea , número dorado , divina proporción …

6. Se representa por la letra griega 𝜑 (fi) (en minúscula) y  (fl) (en mayúscula). Es un número irracional. Es la inicial del nombre del escultor griego Fidias (arquitecto del Partenón). Fi (, 𝜑) también se representa con la letra griega Tau (Τ τ) . El descubrimiento de este número se atribuye a la escuela pitagórica (utilizan el signo de las 5 puntas).

7. Fidias (490-430 a.C): escultor y matemático griego que ayudó en la construcción de Partenón. Se dice que aplicó la proporción áurea en su escultura. Los griegos de la Antigüedad Clásica creían que la proporción conducía a la salud y a la belleza

8. Platón (427-347 a.C): descubrió 5 posibles cuerpos regulares que podían constituir la base de la estructura armónica del universo, sus dimensiones las determinan la proporción áurea.

9. Euclides (325-265 a.C): en sus Elementos formuló la primera definición que se conserva de la proporción áurea.

10. Fibonacci (1170-1250): ideó la sucesión que guarda relación con la proporción áurea. Luca Pacioli (1445-1517): en su libro La Divina Proporción , expone por qué la proporción áurea debe llamarse divina proporción.

11. Kepler (1571-1630): calificó la proporción áurea de piedra preciosa. Charles Bonnet (1720-1793): descubrió en la filotaxia de plantas la sucesión de Fibonacci Martin Ohm (principios del XIX): fue el primero en emplear la sección áurea para describir la proporción áurea

12. Eduard Lucas (1842-1891): bautizó oficialmente la sucesión de Fibonacci. Mark Barr (siglo XX): le puso el nombre fi a la proporción áurea Roger Penrose (1931): halló una simetría de la proporción áurea en los cuasicristales.

13. Los pitagóricos cultivaron el concepto de número, principio de toda proporción, orden y armonía en el universo; estableciendo así una base para las matemáticas y en geometría su descubrimiento fue: el teorema de Pitágoras (el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los catetos).

14. El símbolo de los pitagóricos es la estrella pentagonal o pentágono estrellado; y es este símbolo se encontró el número de oro:

15. Fibonacci nos tragó los números arábigos. La sucesión de Fibonacci es: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144… donde a partir de los 2 primeros términos, los restantes se forman sumando los dos anteriores. Cada vez que dividimos un número por el anterior nos da .

16. Se dice que esta sucesión surgió como respuesta al problema de calcular el número de crías que podía tener una pareja de conejos. Jóvenes al cabo de meses, teniendo en cuenta: a) Los conejos tardan un mes para ser adultos y procrearse. b) Todos los meses pueden procrearse. c) Suponiendo que en cada procreación nace una pareja y no muere ninguno.

17. Solución:

18. La sucesión áurea fue empleada en el arte del antiguo Egipto : Pirámide de Keops .

19. En la antigua Grecia , se utilizó para establecer proporciones de los templos (fachada y planta): Partenón ; la estatúa Doríforo (su altura es 8 veces la cabeza) del escultor griego Policleto.

20. En Asia Menor encontramos un pentágono regular en la Tumba Rupestre de Mira .

21. En Francia se construyó la catedral de Notre -Dame con rectángulos áureos en su fachada Occidental.

22. Leonardo Da Vinci : en la Gioconda , utilizó rectángulos áureos para plasmar el rostro de Mona Lisa. Se basó en las proporciones humanas para crear el hombre de Vitruvio .

23. Alberto Durero , el más conocido artista alemán del Renacimiento. En su libro Instrucción sobre la medida con regla y compás de figuras planas y sólidas, nos muestra como trazar espirales con regla y compás, destacando: la Espiral de Durero , utilizando en ella el número de oro.

24. Velázquez también utilizó la proporción áurea en sus obras: Las Meninas

25. Dalí se basó en el pentagrama místico pitagórico para la creación de Leda Atómica ; utilizó el dodecaedro en: La Última Cena .

26. Hoy en día , lo podemos distinguir en el edificio de la ONU en Nueva York (prisma rectangular cuya cara mayor sigue las citadas proporciones).

27. En nuestra vida cotidiana estamos rodeados de rectángulos áureos: DNI, tarjetas de crédito, cajetillas de tabaco …

28. En la música , encontramos la proporción áurea en varias sonatas de Mozart, la Quinta Sinfonía de Beethoven, Bach…

29. La proporción áurea está ligada a la naturaleza (sucesión de Fibonacci, espiral áurea, rectángulo de oro…) aparece en el crecimiento de plantas, distribución de las hojas de un tallo, formación de caracolas, en insectos y animales…

30. En los insectos: Proporción divina en la morfología de hormigas, mariposas, saltamontes, abejas…

31. En los pájaros: Guardan una relación de proporción áurea entre cabeza y cuerpo; las águilas descienden hacia su presa dibujando una espiral áurea en el cielo

32. En las caracolas: En Filipinas el molusco: el Nautilus Los ammonites (fósiles de hace millones de años nos dejaron sus espirales gravadas en piedras. La concha de caracol forma espiral aúrea

33. En el hombre: Luca Pacioli propone al hombre perfecto: relación entre la altura del hombre y la distancia del ombligo a la mano es el número áureo; también aparece la longitud de la cabeza y su anchura…

34. En las plantas: En la filotaxia (ramas y hojas se distribuyen buscando luz solar) esta distribución sigue sucesiones: Los girasoles tienen 55 espirales en un sentido y 89 en otro, o bien 89 y 144 (sucesión de Fibonacci).

35. Las margaritas presentan las semillas en forma de 21 y 34 espirales. En fruta como la piña con sus piñones coinciden con la sucesión de Fibonacci

36. El astrónomo Johannes Kepler descubrió la naturaleza elíptica de la órbitas de los planetas alrededor del sol, mencionó la divina proporción: El teorema de Pitágoras La división de una línea entre el extremo y su proporcionalidad. El primero lo comparó con una medida de oro y el segundo como una joya de oro.

38. Por lo que deducimos:

39. http://www.youtube.com/watch?v=7h8dNH9Xnfg http://rt000z8i.erasmas.net/El%20numero%20de%20oro.htm http://www.ing.unic.edu.ar/publicaciones/doc_de.../numero_de_oro.doc . http ://canalhypatia/ladivinaproporción.blogspot.com/introducion-la-proporcion-urea.html http://debuxoiesdesada.blogspot.com / http:// es.wikipedia.org www.portalplanetasedna.com.ar/divina_proporcion.htm