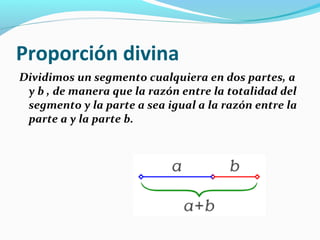
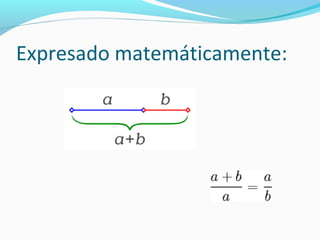
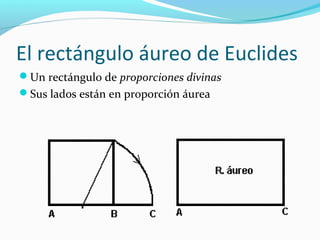
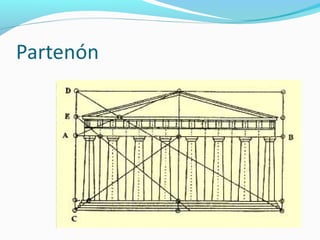
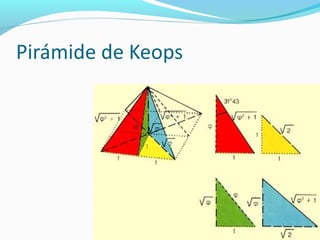
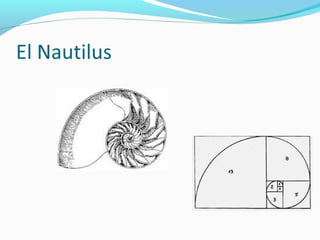
El documento describe la proporción áurea y su presencia en el arte, la naturaleza y la música a lo largo de la historia. Se define matemáticamente como una proporción entre dos segmentos divididos de tal forma que la relación entre los segmentos es la misma que entre sus partes. Los artistas desde la antigüedad la han utilizado intuitivamente en obras como la Venus de Milo y composiciones de Mozart y Beethoven parecen seguir esta proporción de forma no intencional.

1. • Número de Oro.
• El rectángulo áureo de Euclides.
• En el Arte.
• En la Naturaleza.
• En la Música.

2. Proporciones
Desde la antigüedad,
los artistas se
ocuparon de
encontrar una razón
que produjera una
forma ideal para
representar la belleza
en las figuras y en la
arquitectura.

3. Esa razón es la proporción ideal entre
los elementos que integran la obra
artística.
Los artistas la utilizan desde la más
remota antigüedad.
Los griegos la desarrollaron en fórmula
matemática.
No fue regla arbitraria establecida al
azar, sino fruto de un constante
estudio de la naturaleza.

4. Vieron que en la naturaleza, y en la misma figura
humana, se daba esta proporción de líneas
constante.
Pensaron que era obra de Dios al dar el ser a sus
criaturas.

5. Se conoce ya de su existencia en
los pentágonos regulares y
pentáculos de las tabletas
sumerias de alrededor del
3200 a. C.

6. Proporción divina
Dividimos un segmento cualquiera en dos partes, a
y b , de manera que la razón entre la totalidad del
segmento y la parte a sea igual a la razón entre la
parte a y la parte b.

7. Expresado matemáticamente:

8. Para los de matemáticas:

9. Número de oro
Su valor es de 1,61803 ...
Se le representa con una letra griega: Φ
En honor a Fidias, escultor griego

10. El rectángulo áureo de Euclides
Un rectángulo de proporciones divinas
Sus lados están en proporción áurea

13. Leonardo usó el número Φ
Εl cociente entre el
lado del cuadrado y
el radio de la
circunferencia que
tiene por centro el
ombligo, es el
número de oro

14. El pentagrama
Existe la relación del número
áureo también en el
pentagrama, un símbolo
pagano, más tarde acogido por
la iglesia católica para
representar a la Virgen María.

15. En el cuerpo humano
La comprobación empírica de los
humanistas en el siglo XV determinó
que existía una relación: Φ, si se
dividia el resultado de medir, desde el
hombro hasta la punta de los dedos de
la mano extendida, por el resultado de
la medida desde el codo hasta la punta
extendida de los dedos.

16. Lo mismo ocurría dividiendo la
medidas desde la cadera al suelo
entre la medida desde la rodilla al
suelo.
O también existía la proporción Φ
al dividir la altura total por la
medida resultante desde el ombligo
al suelo.

17. En el arte
Existen relaciones
basadas en la
sección áurea en
algunas de las más
célebres estatuas
griegas como el
Hermes de
Praxíteles (390-
330 a. C.).

18. Aparece en la Venus
de Milo

19. El cuadro de Dalí Leda atómica, pintado en 1949,
sintetiza siglos de tradición matemática y
simbólica, especialmente pitagórica.
Se trata de una filigrana basada en la proporción
áurea, pero elaborada de tal forma que no es
evidente para el espectador.
En el boceto de 1947 se advierte la meticulosidad del
análisis geométrico realizado por Dalí basado en el
pentagrama místico pitagórico.

25. En la música
En varias sonatas para piano de Mozart, la
proporción entre el desarrollo del tema y su
introducción es la más cercana posible a la razón
áurea. ¿Intuición?
Tampoco se sabe si fue consciente de ello, pero en
su Quinta Sinfonía Beethoven distribuye el
famoso tema siguiendo la sección áurea.

26. En la música
Autores como Bártok, Messiaen y Stockhausen,
entre otros, compusieron obras cuyas unidades
formales se relacionan (a propósito) con la sección
áurea.