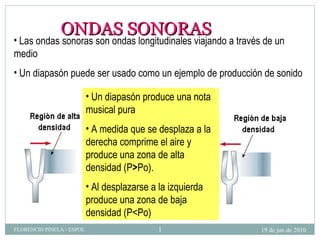
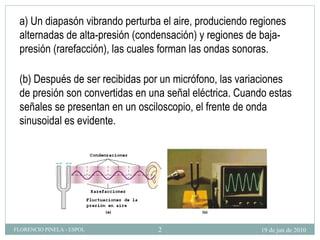
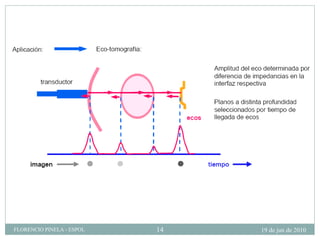
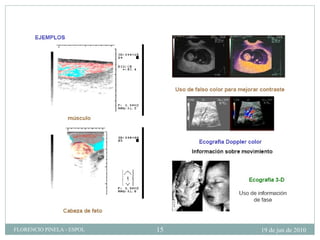
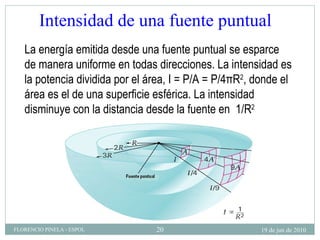
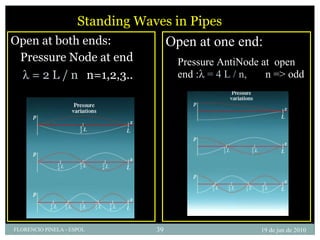
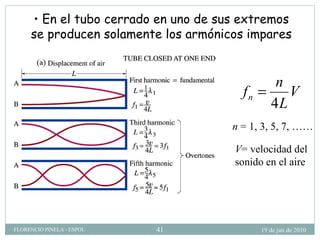
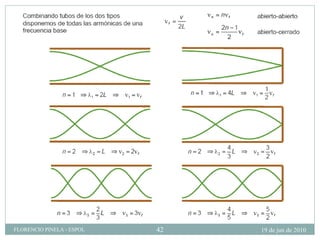
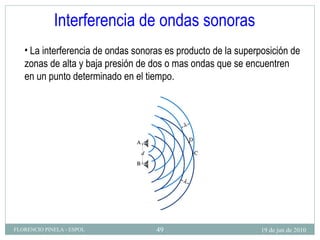
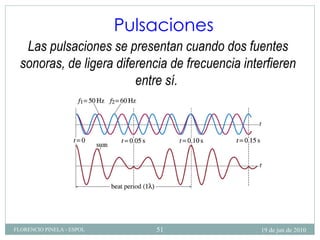
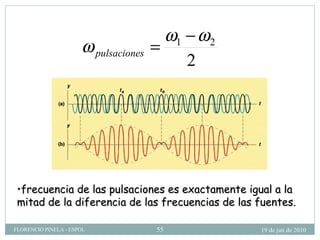
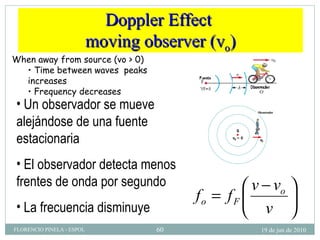
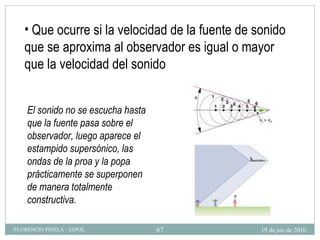
1) El documento describe las ondas sonoras y cómo se producen a través de la vibración de un diapasón. 2) Un diapasón vibrando perturba el aire y produce regiones alternadas de alta y baja presión que forman las ondas sonoras. 3) El documento también discute la velocidad del sonido en diferentes medios y cómo se ven afectadas las ondas de sonido al pasar de un medio a otro.

1. ONDAS SONORAS Las ondas sonoras son ondas longitudinales viajando a través de un medio Un diapasón puede ser usado como un ejemplo de producción de sonido Un diapasón produce una nota musical pura A medida que se desplaza a la derecha comprime el aire y produce una zona de alta densidad (P > Po) . Al desplazarse a la izquierda produce una zona de baja densidad (P <Po) 19 de jun de 2010 FLORENCIO PINELA - ESPOL

2. a) Un diapasón vibrando perturba el aire, produciendo regiones alternadas de alta-presión (condensación) y regiones de baja-presión (rarefacción), las cuales forman las ondas sonoras. (b) Después de ser recibidas por un micrófono, las variaciones de presión son convertidas en una señal eléctrica. Cuando estas señales se presentan en un osciloscopio, el frente de onda sinusoidal es evidente. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

3. A medida que el diapasón continúa vibrando, una sucesión de compresiones y rarefacciones se propagan desde el diapasón Una curva senoidal puede ser usada para representar la onda longitudinal. Las crestas corresponden a las compresiones y los valles a las rarefacciones 19 de jun de 2010 FLORENCIO PINELA - ESPOL

4. Speed of Sound Recall for pulse on string: For fluids: (F) Tensión de la cuerda (  )Densidad lineal de la cuerda (  ) Módulo de compresibilidad volumétrica (  ) Densidad volumétrica 19 de jun de 2010 FLORENCIO PINELA - ESPOL Medium Speed (m/s) Air 343 Helium 972 Water 1500 Steel 5600

5. Helium ACTs A sound wave having frequency f 0 , speed v 0 and wavelength  0 , is traveling through air when in encounters a large helium-filled balloon. Inside the balloon the frequency of the wave is f 1 , its speed is v 1 , and its wavelength is  1 Compare the speed of the sound wave inside and outside the balloon A. v 1 < v 0 B. v 1 = v 0 C. v 1 > v 0 Compare the frequency of the sound wave inside and outside the balloon A. f 1 < f 0 B. f 1 = f 0 C. f 1 > f 0 Compare the wavelength of the sound wave inside and outside the balloon A.          C     19 de jun de 2010 FLORENCIO PINELA - ESPOL

6. Velocity ACT A sound wave having frequency f 0 , speed v 0 and wavelength  0 , is traveling through air when in encounters a large helium-filled balloon. Inside the balloon the frequency of the wave is f 1 , its speed is v 1 , and its wavelength is  1 Compare the speed of the sound wave inside and outside the balloon 1. v 1 < v 0 2. v 1 = v 0 3. v 1 > v 0 19 de jun de 2010 FLORENCIO PINELA - ESPOL V 1 =965m/s V 0 =343m/s

7. Frequency ACT A sound wave having frequency f 0 , speed v 0 and wavelength  0 , is traveling through air when in encounters a large helium-filled balloon. Inside the balloon the frequency of the wave is f 1 , its speed is v 1 , and its wavelength is  1 Compare the frequency of the sound wave inside and outside the balloon 1. f 1 < f 0 2. f 1 = f 0 3. f 1 > f 0 Time between wave peaks does not change! 19 de jun de 2010 FLORENCIO PINELA - ESPOL f 1 f 0

8. Wavelength ACT A sound wave having frequency f 0 , speed v 0 and wavelength  0 , is traveling through air when in encounters a large helium-filled balloon. Inside the balloon the frequency of the wave is f 1 , its speed is v 1 , and its wavelength is  1 Compare the wavelength of the sound wave inside and outside the balloon 1.  1 <  0 2.  1 =  0 3.  1 >  0 19 de jun de 2010 FLORENCIO PINELA - ESPOL  0  1  = v / f

9. ONDAS ESFERICAS Una onda esférica se propaga radialmente hacia el exterior de la fuente oscilante La energía se propaga de manera uniforme en todas direcciones 19 de jun de 2010 FLORENCIO PINELA - ESPOL

10. REPRESENTACION DE LAS ONDAS Los frentes de onda son los arcos concéntricos. La distancia entre frentes de ondas consecutivos es una longitud de onda . Los rayos son líneas que apuntan desde la fuente perpendicular a los frente de ondas 19 de jun de 2010 FLORENCIO PINELA - ESPOL

11. Los frente de onda relativamente alejados de la fuente se pueden considerar como frente de ondas planos. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

12. Espectro de frecuencias del sonido La región audible del sonido para el oído se encuentra entre 20 Hz y 20 kHz. Por debajo es la región infrasónica, y por sobre es la región ultrasónica. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

13. Uso del Ultrasonido El ultrasonido generado por transductores, el que convierte oscilaciones eléctricas en vibraciones mecánicas y viceversa, es transmitido a través del tejido y reflejado de las estructuras internas. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

14. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

15. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

16. Anatomía del oído humano El oído convierte la variación de presión en el aire en impulsos eléctricos nerviosos que son interpretados por el cerebro como sonido 19 de jun de 2010 FLORENCIO PINELA - ESPOL

17. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

18. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

19. Intensidad del Sonido La intensidad o volumen es una sensación en la conciencia del ser humano. La intensidad es la energía que transporta la onda por unidad de tiempo a través de una unidad de área. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

20. Intensidad de una fuente puntual La energía emitida desde una fuente puntual se esparce de manera uniforme en todas direcciones. La intensidad es la potencia dividida por el área, I = P/A = P/4 π R 2 , donde el área es el de una superficie esférica. La intensidad disminuye con la distancia desde la fuente en 1/R 2 19 de jun de 2010 FLORENCIO PINELA - ESPOL

21. Varias intensidades de sonido Umbral de audición: sonido más tenue que la mayoría de los humanos puede escuchar, 1x10 -12 W/m 2 Umbral del dolor: máxima intensidad que la mayoría de los humanos puede tolerar, 1 W/m 2 19 de jun de 2010 FLORENCIO PINELA - ESPOL

22. La escala del sonido (El decibel como nivel de intensidad) La sensación de volumen en el oído humano es logarítmica El nivel de intensidad o el nivel del sonido en decibeles,  19 de jun de 2010 FLORENCIO PINELA - ESPOL

23. I o es el umbral de audibilidad: I o = 1.0x10 -12 W/m 2 Umbral de audibilidad es 0 db Umbral del dolor es 120 db Turbina de un avión del orden de 150 db 19 de jun de 2010 FLORENCIO PINELA - ESPOL

24. Log 10 Review Log 10 (1) = 0 Log 10 (10) = 1 Log 10 (100) = 2 Log 10 (1,000) = 3 Log 10 (10,000,000,000) = 10 19 “ the decibel conversion” 19 de jun de 2010 FLORENCIO PINELA - ESPOL

25. Niveles de intensidad del sonido y la escala de Decibeles 19 de jun de 2010 FLORENCIO PINELA - ESPOL

26. Intensity and Loudness Intensity if the power per unit area. I = P / A Units Watts/m 2 For Sound Waves I = p 0 2 / (2  v) Proportional to p 0 2 note Energy goes as A 2 Loudness (Decibels) Loudness perception is logarithmic Threshold for hearing I 0 = 10 -12 W/m 2  = (10 dB) log 10 ( I / I 0 )  2 –  1 = (10 dB) log 10 (I 2 /I 1 ) 19 de jun de 2010 FLORENCIO PINELA - ESPOL

27. Decibels ACT If 1 person can shout with loudness 50 dB. How loud will it be when 100 people shout? 1) 52 dB 2) 70 dB 3) 150 dB 19 de jun de 2010 FLORENCIO PINELA - ESPOL

28. Decibels ACT If 1 person can shout with loudness 50 dB. How loud will it be when 100 people shout? 1) 52 dB 2) 70 dB 3) 150 dB  100 –  1 = (10 dB) log 10 (I 100 /I 1 )  100 = 50 + (10 dB) log 10 (100/1)  100 = 50 + 20 22 19 de jun de 2010 FLORENCIO PINELA - ESPOL

29. Intensity Preflight Suppose you are standing a distance D away from a speaker that is radiating sound in a spherically uniform way. You walk away from the speaker until the loudness of the sound is reduced by a factor of two. About how far from the speaker are you now? (neglect any reflections from the ground) 1. 10D 2. 4D 3. 3D 4. 2D 19 de jun de 2010 FLORENCIO PINELA - ESPOL

30. Speaker radiating power P Changing I by 10 will change loudness by 2 We want I 1 /I 2 = 10 19 de jun de 2010 FLORENCIO PINELA - ESPOL I 1 = P/(4  D 1 2 ) D 1 I 2 = P/(4  D 2 2 ) D 2

31. Intensity ACT Recall Intensity = P/A. If you are standing 6 meters from a speaker, and you walk towards it until you are 3 meters away, by what factor has the intensity of the sound increased? 1) 2 2) 4 3) 8 19 de jun de 2010 FLORENCIO PINELA - ESPOL

32. Intensity ACT Recall Intensity = P/A. If you are standing 6 meters from a speaker, and you walk towards it until you are 3 meters away, by what factor has the intensity of the sound increased? 1) 2 2) 4 3) 8 Area goes as d 2 so if you are ½ the distance the intensity will increase by a factor of 4 27 19 de jun de 2010 FLORENCIO PINELA - ESPOL Speaker radiating power P I 1 = P/(4  D 1 2 ) D 1 I 2 = P/(4  D 2 2 ) D 2

33. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

34. El nivel de intensidad de conversación a 1 m de distancia es de 60 dB 19 de jun de 2010 FLORENCIO PINELA - ESPOL

35. Curvas de respuesta de frecuencia El umbral de audición es fuertemente dependiente de la frecuencia. El oído humano es más sensible a los ~ 4000 Hz Cuando se aumenta el volumen del sonido, todas las frecuencias se escuchan igualmente bien. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

36. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

37. Cuerdas Vibratorias y Columnas de Aire Frecuencias naturales de oscilación de una cuerda tensa 19 de jun de 2010 FLORENCIO PINELA - ESPOL

38. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

39. Standing Waves in Pipes Open at both ends: Pressure Node at end   = 2 L / n n=1,2,3.. Open at one end: Pressure AntiNode at open end :  = 4 L / n, n => odd 19 de jun de 2010 FLORENCIO PINELA - ESPOL

40. En el tubo abierto en ambos extremos se produce toda la serie armónica V= velocidad del sonido en el aire 19 de jun de 2010 FLORENCIO PINELA - ESPOL

41. En el tubo cerrado en uno de sus extremos se producen solamente los armónicos impares V = velocidad del sonido en el aire n = 1, 3, 5, 7, …… 19 de jun de 2010 FLORENCIO PINELA - ESPOL

42. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

43. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

44. Organ Pipe Example A 0.9 m organ pipe (open at both ends) is measured to have it’s first harmonic at a frequency of 382 Hz. What is the speed of sound in the pipe? L=0.9 m 19 de jun de 2010 FLORENCIO PINELA - ESPOL

45. Organ Pipe Example A 0.9 m organ pipe (open at both ends) is measured to have it’s first harmonic at a frequency of 382 Hz. What is the speed of sound in the pipe? Pressure Node at each end.  = 2 L / n n=1,2,3..  = L for first harmonic (n=2) f = v /  v = f  = (382 s -1 ) (0.9 m) = 343 m/s 19 de jun de 2010 FLORENCIO PINELA - ESPOL

46. Resonance ACT What happens to the fundamental frequency of a pipe, if the air (v=343 m/s) is replaced by helium (v=972 m/s)? 1) Increases 2) Same 3) Decreases f = v/  19 de jun de 2010 FLORENCIO PINELA - ESPOL

47. Conociendo la posición de resonancia se puede determinar la frecuencia de vibración de un diapasón Conociendo la frecuencia del diapasón se puede determinar la velocidad del sonido en el aire. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

48. Constructive interference Destructive interference Interference and Superposition 19 de jun de 2010 FLORENCIO PINELA - ESPOL

49. Interferencia de ondas sonoras La interferencia de ondas sonoras es producto de la superposición de zonas de alta y baja presión de dos o mas ondas que se encuentren en un punto determinado en el tiempo. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

50.  d sen  d Interferencia Constructiva d sen  = m λ d sen  = (m+1/2) λ Interferencia destructiva 19 de jun de 2010 FLORENCIO PINELA - ESPOL

51. Las pulsaciones se presentan cuando dos fuentes sonoras, de ligera diferencia de frecuencia interfieren entre sí. Pulsaciones 19 de jun de 2010 FLORENCIO PINELA - ESPOL

52. Superposition & Interference Consider two harmonic waves A and B meeting at x=0 . Same amplitudes, but  2 = 1.15 x  1 . The displacement versus time for each is shown below: A(  1 t) B(  2 t) C(t) = A(t) + B(t) 19 de jun de 2010 FLORENCIO PINELA - ESPOL CONSTRUCTIVE INTERFERENCE DESTRUCTIVE INTERFERENCE

53. Beats Can we predict this pattern mathematically? Of course! Just add two cosines and remember the identity: where and cos(  L t) 19 de jun de 2010 FLORENCIO PINELA - ESPOL

54. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

55. frecuencia de las pulsaciones es exactamente igual a la mitad de la diferencia de las frecuencias de las fuentes. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

56. Preflight 1 As a police car passes you with its siren on, the frequency of the sound you hear from its siren 1) Increases 2) Decreases 3) Same 19 de jun de 2010 FLORENCIO PINELA - ESPOL

57. El efecto Doppler El efecto Doppler se presenta cuando hay movimiento relativo entre una fuente de ondas y un observador 19 de jun de 2010 FLORENCIO PINELA - ESPOL

58. Aunque el efecto Doppler es experimentado comúnmente con ondas sonoras, este fenómeno es común para todas las ondas 19 de jun de 2010 FLORENCIO PINELA - ESPOL

59. Un observador se está moviendo hacia una fuente estacionaria Debido a su movimiento, el observador detecta un mayor número de frentes de onda La frecuencia escuchada se incrementa Doppler Effect moving observer (v o ) When moving toward source (vo < 0) Time between waves peaks decreases Frequency increases 19 de jun de 2010 FLORENCIO PINELA - ESPOL

60. Un observador se mueve alejándose de una fuente estacionaria El observador detecta menos frentes de onda por segundo La frecuencia disminuye Doppler Effect moving observer (v o ) When away from source (vo > 0) Time between waves peaks increases Frequency decreases 19 de jun de 2010 FLORENCIO PINELA - ESPOL

61. A medida que la fuente se mueve hacia el observador (A), la longitud de onda disminuye y la frecuencia aumenta A medida que la fuente se mueve alejándose del observador (B), la longitud de onda se incrementa y la frecuencia disminuye Doppler Effect moving source v s When source is coming toward you (v s > 0) Distance between waves decreases Frequency increases When source is going away from you (v s < 0) Distance between waves increases Frequency decreases 19 de jun de 2010 FLORENCIO PINELA - ESPOL

62. ¿Cuál sería la expresión para la frecuencia percibida por el “observador” si tanto la fuente como el observador se encuentran en movimiento? ¿Podría determinar la velocidad con que se mueve el vehiculo? 19 de jun de 2010 FLORENCIO PINELA - ESPOL

63. Doppler Effect When source is moving toward you: Distance between waves decreases Frequency increases When source is moving away from you: Distance between waves increases Frequency decreases When moving toward source: Velocity of waves increases Frequency increases When moving away from source: Velocity of waves decreases Frequency decreases 19 de jun de 2010 FLORENCIO PINELA - ESPOL

64. Doppler ACT A: You are driving along the highway at 65 mph, and behind you a police car, also traveling at 65 mph, has its siren turned on. B: You and the police car have both pulled over to the side of the road, but the siren is still turned on. In which case does the frequency of the siren seem higher to you? A. Case A B. Case B C. same 19 de jun de 2010 FLORENCIO PINELA - ESPOL v s f v o f’ v

65. Ondas de Choque y estampido Sónico Una onda choque resulta cuando la velocidad de la fuente supera a la velocidad de la onda. Los círculos representan los frentes de onda emitidos por la fuente 19 de jun de 2010 FLORENCIO PINELA - ESPOL

66. La velocidad de la fuente y la velocidad del sonido 19 de jun de 2010 FLORENCIO PINELA - ESPOL

67. Que ocurre si la velocidad de la fuente de sonido que se aproxima al observador es igual o mayor que la velocidad del sonido El sonido no se escucha hasta que la fuente pasa sobre el observador, luego aparece el estampido supersónico, las ondas de la proa y la popa prácticamente se superponen de manera totalmente constructiva. 19 de jun de 2010 FLORENCIO PINELA - ESPOL

68. 19 de jun de 2010 FLORENCIO PINELA - ESPOL