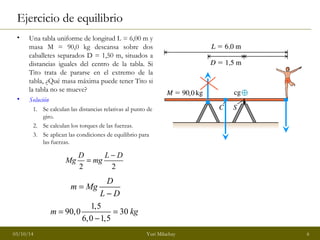
El documento trata sobre el equilibrio de sólidos. Explica que para que un sólido esté en equilibrio, la suma de las fuerzas externas debe ser cero y la suma de los momentos de torsión respecto a cualquier punto debe ser cero. También habla sobre el centro de gravedad y cómo calcularlo, y presenta varios ejemplos de problemas de equilibrio resueltos.

1. Semana 4 Sesión 1
Equilibrio
Equilibrio. Condiciones de equilibrio.
Física 1

2. Centro de gravedad
• El cálculo del torque del peso agrega una
variable a la resolución de la condición de
equilibrio de un cuerpo: es preciso saber la
ubicación del centro de gravedad; esto es, el
punto donde se concentra todo el peso del
cuerpo.
• Recordemos la definición de centro de masa
r
å
å
mr
i i
i
=
CM m
i
i
• Si g tiene el mismo valor en todos los puntos
del cuerpo, el centro de gravedad es idéntico
al centro de masa.
o CM t = r ´ Mg r r r
• El torque que ejerce el peso sobre un sólido
se puede calcular asumiendo que todo su
peso actúa en su centro de gravedad.
El centro de masa es el promedio ponderado de
las posiciones por la masa
El centro de gravedad se ubica en el centro de masa si
g no cambia
03/10/14 Yuri Milachay 2

3. Problema 11.1
• Una esfera de 1,00 kg con radio r1=0,080 m
está unida por una varilla ligera de 0,400 m
de longitud a una segunda bola de 2,00 kg
con radio r2=0,100 m . ¿Dónde se encuentra
en centro de gravedad del sistema?
• Solución
• Tomando como referencia el centro de la
esfera pequeña, el centro de gravedad es:
x = (1,00 kg )(0) + (2,00 kg )(0,580 m ) =
0,387
m
3,00 cm
kg
03/10/14 Yuri Milachay 3

4. Condiciones de equilibrio de un sólido
• Para que un sólido se encuentre en equilibrio
debe cumplirse dos condiciones:
a) No debe acelerar de manera rectilínea.
b) No debe rotar con cierta aceleración angular.
• A estas condiciones se le llama “de equilibrio”
y matemáticamente se expresan de la
siguiente manera:
• Condición de equilibrio de traslación
• La suma de las fuerzas externas que actúan
sobre un cuerpo es un vector nulo
åF = 0 r
• Condición de equilibrio rotacional
• La suma de los momentos de torsión
debidos a todas las fuerzas externas que
actúan sobre el cuerpo, respecto a cualquier
punto específico, debe ser cero.
åt = r
Fi 0
o
i
®
T
R ®
w ®
®
T1
1 0 T T R w ®
® ® ® ®
+ + + =
®
0
+ + + = r r r r
R T1 T 0
o o o o
t t w t t
03/10/14 Yuri Milachay 4

5. Centro de gravedad y equilibrio
• ¿En qué caso el torque producido por el peso mantiene al vehículo en equilibrio?
03/10/14 Yuri Milachay 5

6. Ejercicio de equilibrio
• Una tabla uniforme de longitud L = 6,00 m y
masa M = 90,0 kg descansa sobre dos
caballetes separados D = 1,50 m, situados a
distancias iguales del centro de la tabla. Si
Tito trata de pararse en el extremo de la
tabla, ¿Qué masa máxima puede tener Tito si
la tabla no se mueve?
• Solución
1. Se calculan las distancias relativas al punto de
giro.
2. Se calculan los torques de las fuerzas.
3. Se aplican las condiciones de equilibrio para
las fuerzas.
Mg D = mg L - D
2 2
m Mg D
L D
=
-
90,0 1,5 30
m = = kg
-
6,0 1,5
03/10/14 Yuri Milachay 6

7. Ejercicio de equilibrio
• Una revista especializada informa que cierto
auto deportivo tiene 53% de su peso sobre
las ruedas delanteras y el 47% sobre las
traseras, con una distancia entre ejes de 2,46
m. eso implica que la fuerza normal total
sobre las ruedas delanteras es de 0,53 w, y
sobre las traseras, de 0,47 w, donde w es el
peso total. Al espacio entre el eje delantero y
el eje trasero se llama distancia entre ejes.
¿Qué tan adelante del eje trasero está el
centro de gravedad del automóvil?
• Solución
0,53 2,46 0 cg -wL + w´ =
1,30 cg L = m
03/10/14 Yuri Milachay 7

8. Ejercicio de equilibrio
• En la figura se muestra una escalera
uniforme de 5,00 m de longitud y 180,0 N de
peso, un hombre de 800,0 N de peso sube
por la escalera y se detiene después de subir
1/3 de la escalera, si la pared es liza,
determine las fuerzas normal y de fricción
que actúan sobre la base de la escalera.
Calcule el coeficiente de fricción estática
mínimo que evita un deslizamiento en la
base de la escalera. Calcule la magnitud y
dirección de la fuerza de contacto que actúa
sobre la base de la escalera
0
1 -800N ´1,0m -180N ´1,5m + n ´3,0m = 0
2
1 n = 3,6´10 N
2
2 n = 9,8´10 N
2 1 m ´ n = n
m = 0,37
03/10/14 Yuri Milachay 8

9. Ejercicio de equilibrio
• En la figura el hombre esta descansando
después de subir un tramo por la cuerda, El
hombre pesa 700 N, su cuerpo forma un
ángulo de 60° con la pared y su centro de
gravedad esta a 0,85 m de los pies. La fuerza
de la cuerda actúa a 1,30 m de los pies y la
cuerda forma un ángulo de 20° con la
vertical, calcule la tensión y la reacción sobre
los pies del hombre.
• Solución
• Sumatoria de fuerzas en x y y son iguales a
cero.
n -Tsen20° = 0
cos20 700 0 R f + T ° - =
• Sumatoria de torques respecto al punto de
contacto es cero.
R f ®
®
T
n ®
w ®
1,30´T ´ sen140° - 0,85´ 700´ sen60° = 0
T = 6,2´102 N
03/10/14 Yuri Milachay 9

10. Ejercicios para la clase
• Resolver los ejercicios de la pág. 431
• 11.59
• 11.60
• 11.62
• 11.67
03/10/14 Yuri Milachay 10