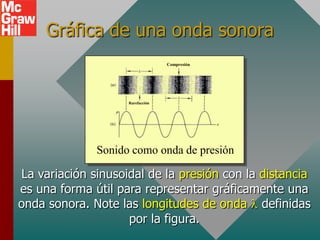
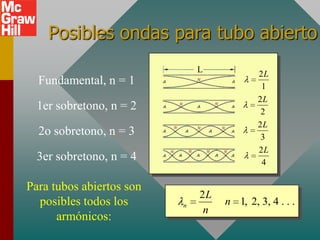
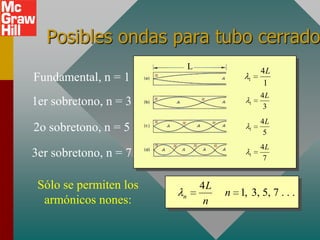
Este documento presenta conceptos clave sobre ondas sonoras, incluyendo su definición como ondas mecánicas longitudinales que requieren un medio elástico, y fórmulas para calcular la velocidad del sonido en diferentes medios. También explica las frecuencias características de ondas estacionarias en tubos abiertos y cerrados.

1. Ondas sonoras
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. Objetivos: Después de
completar este módulo deberá:
• Definir el sonido y resolver problemas
que se relacionan con su velocidad
en sólidos, líquidos y gases.
• Usar condiciones de frontera para
aplicar conceptos relacionados con
frecuencias en tubos abiertos y
cerrados.

3. Definición de sonido
El sonido es una onda
mecánica longitudinal
que viaja a través de
un medio elástico.
Fuente del
sonido:
Muchas cosas vibran en diapasón.
el aire, lo que produce
una onda sonora.

4. ¿Hay sonido en el bosque
cuando cae un árbol?
El sonido es una
perturbación física en
un medio elástico.
Con base en la definición,
HAY sonido en el bosque,
¡ya sea que haya o no un
humano para escucharlo!
¡Se requiere el medio elástico (aire)!

5. El sonido requiere un medio
El sonido de un timbre que sueña disminuye conforme
el aire sale del frasco. No existe sonido sin moléculas de
aire.
Batterías
Bomba de vacío
Frasco al vacío con timbre

6. Gráfica de una onda sonora
Compresión
Rarefacción
Sonido como onda de presión
La variación sinusoidal de la presión con la distancia
es una forma útil para representar gráficamente una
onda sonora. Note las longitudes de onda definidas
por la figura.

7. Factores que determinan la rapidez del
sonido
Las onda mecánicas longitudinales (sonido) tienen
una rapidez de onda que depende de factores de
elasticidad y densidad. Considere los siguientes
ejemplos:
Un medio más denso tiene
mayor inercia que resulta en
menor rapidez de onda.
Un medio que es más elástico acero
se recupera más rápidamente y
resulta en mayor rapidez. agua

8. Rapideces para diferentes
medios
v
Y Módulo de Young, Y
Barra metálica
Densidad del metal,
Módulo
B 4
3 S volumétrico, B
v Sólido Módulo de corte, S
extendido Densidad,
Módulo volumétrico, B
B
v Densidad del fluido,
Fluido

9. Ejemplo 1: Encuentre la rapidez del
sonido en una barra de acero.
= 7800 kg/m3 vs = ¿?
Y = 2.07 x 1011 Pa
Y 2.07 x 1011Pa
v v =5150 m/s
7800 kg/m3

10. Rapidez del sonido en el aire
Para la rapidez del sonido en el aire,
se encuentra que:
= 1.4 para aire
P RT R = 8.34 J/kg mol
B P y
M M = 29 kg/mol
B P RT
v v
M
Nota: La velocidad del sonido aumenta con la
temperatura T.

11. Ejemplo 2: ¿Cuál es la rapidez del
sonido en el aire cuando la temperatura
es 200C?
Dado: = 1.4; R = 8.314 J/mol K; M = 29 g/mol
T = 200 + 2730 = 293 K M = 29 x 10-3 kg/mol
RT (1.4)(8.314 J/mol K)(293 K)
v
M 29 x 10-3kg/mol
v = 343 m/s

12. Dependencia de la temperatura
Nota: v depende de T RT
v
absoluta: M
Ahora v a 273 K es 331
m/s. , R, M no cambian, T
v 331 m/s
de modo que una fórmula 273 K
simple puede ser:
De manera alternativa, está la aproximación que usa 0C:
m/s
v 331 m/s 0.6 0 tc
C

13. Ejemplo 3: ¿Cuál es la
velocidad del sonido en
el aire en un día cuando
la temperatura es de
270C?
T
Solución 1: v 331 m/s
273 K
300 K
T= 270 + 2730 = 300 K; v 331 m/s
273 K
v = 347 m/s
Solución 2: v = 331 m/s + (0.6)(270C); v = 347 m/s

14. Instrumentos musicales
Las vibraciones en
una cuerda de violín
producen ondas
sonoras en el aire.
Las frecuencias
características se
basan en la longitud,
masa y tensión del
alambre.

15. Columnas de aire en vibración
Tal como para una cuerda en vibración, existen
longitudes de onda y frecuencias características
para ondas sonoras longitudinales. Para tubos se
aplican condiciones de frontera:
El extremo abierto de un tubo Tubo abierto
debe se un antinodo A en A A
desplazamiento.
El extremo cerrado de un tubo Tubo cerrado
debe ser un nodo N en N A
desplazamiento.

16. Velocidad y frecuencia de onda
El periodo T es el tiempo para moverse una distancia de
una longitud de onda. Por tanto, la rapidez de onda es:
1
v pero T de modo que v f
T f
La frecuencia f está s-1 o hertz (Hz).
La velocidad de cualquier onda es el producto
de la frecuencia y la longitud de onda:
v
v f f

17. Posibles ondas para tubo abierto
L 2L
Fundamental, n = 1 1
2L
1er sobretono, n = 2 2
2L
2o sobretono, n = 3 3
2L
3er sobretono, n = 4 4
Para tubos abiertos son
2L
posibles todos los n n 1, 2, 3, 4 . . .
n
armónicos:

18. Frecuencias características para
tubo abierto
L 1v
Fundamental, n = 1 f
2L
2v
1er sobretono, n = 2 f
2L
3v
2o sobretono, n = 3 f
2L
4v
3er sobretono, n = 4 f
2L
Para tubos abiertos son
nv
posibles todos los fn n 1, 2, 3, 4 . . .
2L
armónicos:

19. Posibles ondas para tubo cerrado
L 4L
Fundamental, n = 1 1
1
4L
1er sobretono, n = 3 1
3
4L
2o sobretono, n = 5 1
5
4L
3er sobretono, n = 7 1
7
Sólo se permiten los 4L
n n 1, 3, 5, 7 . . .
armónicos nones: n

20. Posibles ondas para tubo cerrado
L 1v
Fundamental, n = 1 f1
4L
3v
1er sobretono, n = 3 f3
4L
5v
2o sobretono, n = 5 f5
4L
7v
3er sobretono, n = 7 f7
4L
Sólo se permiten los nv
fn n 1, 3, 5, 7 . . .
armónicos nones: 4L

21. Ejemplo 4. ¿Qué longitud de tubo cerrado se
necesita para resonar con frecuencia fundamental
de 256 Hz? ¿Cuál es el segundo sobretono?
Suponga que la velocidad del sonido es 340 m/s.
Tubo cerrado
nv
N A fn n 1, 3, 5, 7 . . .
4L
L=?
(1)v v 340 m/s
f1 ; L L = 33.2 cm
4L 4 f1 4(256 Hz)
El segundo sobretono ocurre cuando n = 5:
f5 = 5f1 = 5(256 Hz) 2o sobretono = 1280 Hz

22. Resumen de fórmulas para
rapidez del sonido
Barra sólida Sólido extendido Líquido
Y B 4
S B
v v 3 v
Sonido para cualquier gas: Aproximación del
sonido en el aire:
RT m/s
v v 331 m/s 0.6 0 tc
M C

23. Resumen de fórmulas (Cont.)
Para cualquier v
v f f
onda:
Frecuencias características para tubos abiertos y cerrados:
TUBO ABIERTO TUBO CERRADO
nv nv
fn n 1, 2, 3, 4 . . . fn n 1, 3, 5, 7 . . .
2L 4L

24. CONCLUSIÓN:
Ondas sonoras