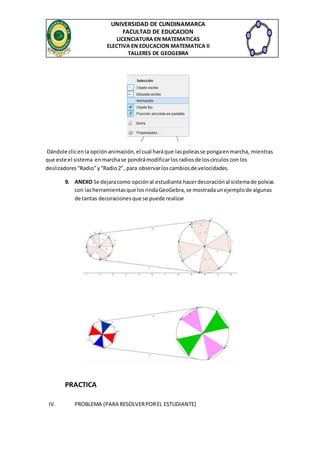
El documento presenta un taller de Geogebra enfocado en la enseñanza de poleas simples a estudiantes de grado octavo, destacando la utilidad de esta herramienta para facilitar la comprensión del tema. Se detallan los métodos y procedimientos para construir y animar sistemas de poleas mediante Geogebra, así como la metodología de evaluación a seguir por los estudiantes. Además, se incluye un enfoque práctico donde los alumnos deben aplicar conceptos teóricos a un problema relacionado con poleas simples.