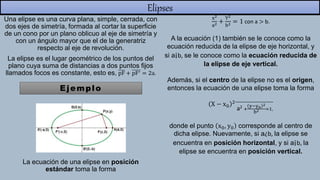
Este documento describe conceptos geométricos como el plano cartesiano, puntos, distancias entre puntos, punto medio, circunferencias, parábolas, elipses e hipérbolas. Explica cómo representar estas figuras geométricas utilizando coordenadas cartesianas y ecuaciones algebraicas. También incluye ejemplos para ilustrar cómo calcular estas propiedades y representarlas gráficamente.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN
UNIVERSITARIA
UNIVERSIDAD POLITÉCNICA TERRITORIAL “Andrés Eloy Blanco”
Plano numérico
Integrante:
Rivero Reyner
C.I. 31.536.135
Sección:
IN0403R

2. Plano numérico
Se conoce como plano cartesiano, a
dos rectas numéricas perpendiculares,
una horizontal y otra vertical, que se
cruzan en un punto llamado origen o
punto cero. El propósito del plano
cartesiano es describir la posición o
ubicación de un punto en el plano
representado por el sistema de
coordenadas.
Sobre cada eje se trazan un conjunto
de marcas de longitud, que sirven de
referencia para ubicar puntos, trazar
figuras, o representar operaciones
matemáticas. O sea, es una
herramienta geométrica para poner
estas últimas en relación gráficamente.
E j empl o
Ubicar los siguientes puntos en el plano
cartesiano:
A (5; 3)
B (-4; -2)
C (-2; 0)
En cada uno de los puntos, ubicamos primero
el valor en el eje X, y luego el valor en el eje Y.
Las ubicaciones de los puntos serían las
siguientes:

3. Distancia
La distancia entre dos puntos no es más que la
longitud del segmento de la recta que los conecta,
el segmento de recta es el pedacito de recta de
un punto a otro, puede ser de manera horizontal,
vertical o oblicua (significa inclinada).
Para estudiar la distancia entre dos punto
consideremos la siguiente figura.
En la figura podemos encontrar dos puntos A(x1,
y1) y B(x2, y2) en el plano cartesiano unidos por
un vector. La magnitud del vector coloreado en
rojo y que une los puntos, es el valor que
representa distancia entre los puntos A(x1, y1) y
B(x2, y2)
Fórmula para calcular la distancia entre dos
puntos y el teorema de Pitágoras
La fórmula para calcular dicha magnitud está dada por
la siguiente expresión:
d(A,B)= x2−x1
2
+ y2 − y1
2.
El valor de esta fórmula puede ser obtenido usando el
Teorema de Pitágoras. Para ello, consideremos el
triángulo rectángulo de vértices: A(x1, y1), B(x2, y2) y
C(x2, y1).
Notemos que el valor de la hipotenusa de este
triángulo es la distancia entre los puntos: A(x1, y1),
B(x2, y2). Ya que la magnitud de los segmentos que
unen A(x1, y1) y C(x2, y1), C(x2, y1) y B(x2, y2)
son (x2 - x1) y (y2 − y1).
El Teorema de Pitágoras afirma que el valor de la
hipotenusa o la distancia entre: A(x1, y1) y B(x2, y2)
es x2−x1
2
+ y2 − y1
2.
Ejemplo

4. Punto Medio
Es el punto que está a la misma distancia de otros dos
puntos o extremos de un segmento.
De manera más general, un punto equidistante en
matemática, es el punto que está a la misma distancia
de dos elementos geométricos, ya sean puntos,
segmentos, rectas, etc.
En el siguiente diagrama tenemos los puntos A y B, los
cuales están unidos por un segmento. El punto C es el
punto medio, ya que está exactamente en la mitad del
segmento. Para calcular la ubicación del punto medio,
simplemente tenemos que medir la longitud del
segmento y dividir por 2.
Ejemplo
Un punto medio puede ser calculado solo
cuando tenemos a un segmento que une a dos
puntos, ya que tiene una ubicación definida. El
punto medio no puede ser calculado para una
línea o un rayo, ya que una línea tiene dos
extremos que se extienden indefinidamente y
un rayo tiene un extremo que se extiende
indefinidamente.
La fórmula para el punto medio de un
segmento es derivada usando las coordenadas
de los puntos extremos del segmento. El punto
medio es igual a la mitad de la suma de las
coordenadas en X de los puntos Y a la mitad
de las coordenadas en Y de los puntos.
Entonces, si es que tenemos los puntos A y B
con las coordenadas A = (x1, y1) y B = (x2, y2)
la fórmula del punto medio es:
Este será expresado como: M = x3, y3

5. Ecuaciones y trazado de circunferencias
La ecuación de la circunferencia describe la
ubicación geométrica de los puntos en el plano que
equidistan de un punto fijo llamado centro. La
ecuación del círculo describe la ubicación
geométrica del conjunto de puntos cuya distancia
al centro es igual o menor que el radio. De esta
manera, la diferencia entre circunferencia y círculo
es esencialmente que la circunferencia es sólo la
línea curva que contiene y bordea, mientras que el
círculo es esa línea más todo lo que contiene
dentro de sí misma.
Hay un caso particular de circunferencia, que tiene
su centro en el origen. La ecuación que la define
se llama ecuación canónica de la
circunferencia: x2+y2 = r2
Si la circunferencia no está centrada en el (0,0), es
posible armar un nuevo sistema de modo tal que el
centro de la circunferencia coincida con el nuevo
origen de coordenadas. Por ejemplo: x − a 2 +
y − B 2 = r2
Si hacemos un cambio de variables:
En las nuevas variables la ecuación queda
expresada en forma canónica: x′2
+ y′2
= r2
Para obtener la ecuación canónica, hicimos una
traslación de ejes, de modo que el centro del nuevo
sistema coincidiera con el centro de la circunferencia:
Ejemplo

6. Parábolas
Una parábola es la ubicación geométrica de los
puntos en el plano que equidistan de un punto fijo
(llamado foco) y una recta fija (llamada directriz).
Por lo tanto, cada punto de una parábola está a la
misma distancia de su foco y directriz.
Dados un punto F (foco) y una recta r (directriz), se
denomina parábola al conjunto de puntos del plano
que equidistan del foco y de la directriz.
Simbólicamente:
P={P(x,y)|d(P,r)=d(P,F)}
Observen que estamos definiendo la parábola como
un conjunto de puntos que verifican cierta propiedad
geométrica, no como la gráfica de una función
cuadrática
Ejemplo
El eje focal es el eje perpendicular a la directriz que
pasa por el foco. Es el eje de simetría de la
parábola.
El punto de la parábola que pertenece al eje focal
se llama vértice.
Para el esquema que realizamos, las coordenadas
del vértice son V(0,0), las del foco F(c,0) y la recta
directriz está dada por r : x = – c. Las coordenadas
de un punto genérico Q que pertenece a la directriz
son (–c,y).

7. Elipses
Una elipse es una curva plana, simple, cerrada, con
dos ejes de simetría, formada al cortar la superficie
de un cono por un plano oblicuo al eje de simetría y
con un ángulo mayor que el de la generatriz
respecto al eje de revolución.
La elipse es el lugar geométrico de los puntos del
plano cuya suma de distancias a dos puntos fijos
llamados focos es constante, esto es, pF + pF′ = 2a.
La ecuación de una elipse en posición
estándar toma la forma
Ejemplo
x2
a2 +
Y2
b2 = 1 con a > b.
A la ecuación (1) también se le conoce como la
ecuación reducida de la elipse de eje horizontal, y
si a¡b, se le conoce como la ecuación reducida de
la elipse de eje vertical.
Además, si el centro de la elipse no es el origen,
entonces la ecuación de una elipse toma la forma
X − x0
2
a2 +
y−y0
2
b2 =1,
donde el punto x0, y0 corresponde al centro de
dicha elipse. Nuevamente, si a¿b, la elipse se
encuentra en posición horizontal, y si a¡b, la
elipse se encuentra en posición vertical.

8. Hipérbola
Una hipérbola es una curva abierta con dos ramas que
se obtiene cortando un cono recto por un plano que no
necesariamente es paralelo al eje de simetría y tiene un
ángulo menor que la generatriz con respecto al eje de
revolución. En geometría analítica, una hipérbola es el
lugar geométrico de los puntos de un plano, tales que el
valor absoluto de la diferencia de sus distancias a dos
puntos fijos, llamados focos, es igual a la distancia entre
los vértices, la cual es una constante positiva. Esta
constante es menor a la distancia entre los focos.
Dados dos puntos F1 y F2 llamados focos, se denomina
hipérbola al conjunto de puntos del plano tales que el
valor absoluto de la diferencia de sus distancias a los
focos es constante.
H={P(x,y)||d(P;F1)–d(P;F2)|=2a =cte}
Ejemplo
Si la distancia entre los focos es d (F1 F2) = 2c,
la condición para que sea una hipérbola es:
C > a > 0
c2 > a2
c2 – a2 = b2
⇒ c2 = a2 + b2

9. Representar gráficamente las ecuaciones de las cónicas
Las cónicas son curvas planas obtenidas mediante la
intersección de un cono con un plano. El ángulo que
forman el plano y el eje del cono, comparado con el
ángulo que forman el eje y la generatriz del cono
determina las distintas clases de cónicas. Además son
sección cónica (o simplemente cónica) a la curva
intersección de un cono con un plano que no pasa por
su vértice. Se clasifican en tres tipos: elipses,
parábolas e hipérbolas.
Una superficie cónica esta engendrada por el giro de
una recta g, que llamamos generatriz, alrededor de
otra recta e, eje, con el cual se corta en un punto V,
vértice.
g = la generatriz, e = el eje, V = el vértice
Ejemplo
Elipse circunferencia Parábola Hipérbola
·La elipse es la sección producida en una superficie cónica de revolución por un plano
oblicuo al eje. a < β < 9O0
· La circunferencia es la sección producida por un plano perpendicular al eje. β =
9O0
, La circunferencia es un caso particular de elipse.
· La parábola es la sección producida en una superficie cónica de revolución por un
plano oblicuo al eje, siendo paralelo a la generatriz. a = β
· La hipérbola es la sección producida en una superficie cónica de revolución por un
plano oblicuo al eje, formando con él un ángulo menor al que forman eje y
generatriz, por lo que incide en las dos hojas de la superficie cónica. a > β