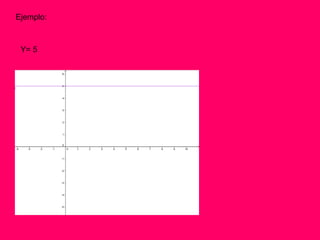
Este documento define y explica diferentes tipos de funciones matemáticas, incluyendo funciones lineales, cuadráticas, cúbicas, constantes e identidades. También describe elementos clave de las funciones como dominio, conjunto de llegada, rango, puntos de corte e inyectivas, sobreyectivas y biyectivas.

1. funciones
Por: Melissa Rascovsky, Melissa Sasson
y Sergio Garrido
Para: Patricia Cáceres
Colegio Colombo Hebreo
Àrea De Matemàticas
Dècimo grado
Bogota d.c

2. FUNCIONES
¿Qué es una función?
Funciones
crecientes,
decrecientes y Gráficas de
tasa de cambio funciones
promedio Elementos de
una función
Transformaciones
de funciones

3. ¿Qué es una función?
Como reemplazar Dominio Representación de
Definición de función una función
Una función es una regla
que asigna a cada
se debe reemplazar el
elemento x en un
numero en la variable Es el conjunto de 1. Verbal
conjunto A exactamente
independiente (x), para elementos que tienen 2. Algebraica
un elemento, llamado
hallar Y. imagen. 3. Visual
f(x), en un conjunto B.
4. Numérica
• El símbolo f(x) se llama el valor de f en x.
• El conjunto A se llama dominio de la función.
• El rango de f es el conjunto de los valores reales
que toma la variable y o f(x).
• La variable independiente (x) es la que no varia
dependiendo de la otra.
• La variable dependiente (y) es la que varia
dependiendo del desplazamiento de x.

4. Elementos de una función
Conjunto de salida
rango Función Sobreyectiva
dominio
Conjunto de llegada Función Biyectiva
Función Inyectiva

5. Gráficas de funciones
Graficación de Ecuaciones de
Graficación funciones definidas funciones
por partes
f(x)= mx + b (se llama función Funciones lineales
lineal) f(x) = mx + b
f(x)= b (se llama función Se define mediante Funciones exponenciales
constante) formulas distintas en su f(x) = x^n
dominio, depende de la
variable independiente Funciones de raiz
x. f(x) = x
Funciones recíprocas
f(x) = 1/x^n
Función valor absoluto
f(x) = IxI

6. Funciones crecientes y
decrecientes, tasa de
promedio
Funciones Funciones Tasa de cambio
crecientes decrecientes promedio
Es la pendiente de la recta secante entre
Se dice que es
creciente cuando
Se dice que x=a y x=b en la grafica de f, es decir, la
es decreciente recta que pasa por (a, f(a)) y (a, f(b)).
la grafica sube, Cuando la grafica baja,
asciende desde (- desciende de (00, -00)
00, 00) en Y. Es decir con respecto a Y.
Tasa de cambio
promedio = cambio en
y / cambio en x

7. Transformaciones de
funciones
Desplazamiento Desplazamiento(acort Desplazamiento( al
Desplazamiento
horizontal ar, alargar) vertical argar o acortar)
vertical
horizontal
Sumar una constante y= f(x + c) desplaza la Para alargar Para alargar una
a la función vertical: grafica c unidades a la verticalmente una grafica grafica se divide
se desplaza hacia izquierda y si se resta se multiplica por un por un numero 1/a,
arriba si la constante desplaza hacia la derecha. numero c mayor que 1. a es mayor que 1.
es positiva y hacia y= f (x - c) Para acortar la grafica se Para acortar la
abajo si es negativa. multiplica por un numero grafica se divide por
a menor que uno pero un numero 1/a,
positivo, entre 1 y 0. cuando a es menor
1, pero positivo.

8. Conjunto
de salida
l conjunto de números que son llamados conjunto A y son las
imágenes, cada elemento debe estar relacionado una ves con un
mento del conjunto de llegada B y posee una imagen. Por lo general reales.

9. Conjunto
de llegada
Es el conjunto de números del conjunto B, llamados imágenes, y están
relacionados con los elementos del conjunto A. Generalmente son reales.

10. rango
Es el conjunto de imágenes, el conjunto de números que se
relacionan una ves con los elementos del conjunto A.

11. dominio
Es el conjunto de pre imágenes, el conjunto de números que del
conjunto A están relacionados una ves con un solo elemento del
conjunto B. Generalmente reales.

12. Función si todos los elementos del dominio están
relacionados una sola vez con un elemento
del rango. No puede haber dos o mas
inyectiva elementos del dominio con la misma
imagen.
cuando f(x) = f(y), x = y.
Ejemplo: f(x) = x+5 del conjunto de los números reales es una función Inyectiva
1
A
2
B
3
C
4
D
5

13. Función
sobreyectiva
F(x)=B si a cada elemento del dominio le
corresponde un elemento del rango.
Ejemplo: la función f(x) = 6x del conjunto de
los números naturales al de los números pares
es Sobreyectiva.
1 D
2 F
3 G
4 H
5 i

14. Función 1
2
-1
-2
biyectiva 3
4
5
-3
-4
-5
Todos los elementos del conjunto A tienen una imagen distinta en el
conjunto B (Inyectiva), cada elemento del conjunto A le corresponde un
elemento del conjunto B (Sobreyectiva). Es Inyectiva y Sobreyectiva a la
ves.
Ejemplo: La función f(x) = 3x del conjunto de números reales es
Inyectiva y Sobreyectiva. Por lo tanto es Biyectiva.

15. Funciones
Polinómicas Otras
Lineal Constante Grado par Grado impar
Cuadrática
Lineal Cúbica
Afín Lineal Identidad Valor
absoluto
Logarítmica
Racional
A trozos
Exponencial
Trigonométrica

16. Polinómicas
Son aquellas funciones que surgen de evaluar los polinomios sobre las variables en las
que están definidos.
Dominio= Conjunto de Salida= IR
Conjunto de llegada= IR
donde es un polinomio en , , es decir, una suma finita de
potencias de multiplicados por coeficientes reales.

17. Ejemplo:

18. Funciones de Son funciones que como
grado par máximo grado de un
término es un número
par. Está dada por la
ecuación:
Conjunto de salida=Dominio=IR Punto de corte con y= igualando x a 0
Conjunto de llegada=IR Puntos de corte con x= igualando y a 0
Rango =(depende de la función, de Vértice= +-b/2a
sus máximos y mínimos.) Conjunto de salida=Dominio=IR
Conjunto de llegada =IR Rango= máximos
y mínimos.
Por lo general es la función
F(x) ≥0 en x IR positivos.
cuadrática.
F(x) ≤0 en x IR negativos

19. Funciones de Son funciones en las cuales el máximo grado
de un término es un número impar . Está
grado impar dada por la ecuación:
Función cúbica Conjunto de
salida=Dominio=IR
Punto de corte con y= igualando x a Conjunto de llegada=IR
0 Rango =IR
Punto de corte con x= igualando y a
0 en la función constante el
Conjunto de salida=Dominio=IR rango es la variable f(x)=a
Conjunto de llegada =IR
Rango= IR Se divide en función cúbica y
lineal.
F(x) ≥0 en x IR positivos
F(x) ≤ 0 en x IR negativos

20. Lineal
Un polinomio de primer grado de una variable real es una función matemática de la
forma:
F(x)= mx + b
donde m y b son constantes. La función lineal , pasa por el punto (0,0) como origen a
diferencia de la función lineal afín.
Una función lineal de una única variable independiente x suele escribirse en la forma
siguiente
•m es denominada la pendiente de la recta.
•b es la ordenada en el origen, el valor de y para x= 0, es el punto (0,b).

21. Ejemplo:
Pendiente:
Y = 5x

22. Afín
Una función lineal afín es aquella cuya expresión matemática viene dada por:
Y= mx + n
donde x e y son variables, m una constante que se denomina pendiente y n otra
constante denominada ordenada en el origen. Su gráfica es una recta que corta al eje de
ordenadas en .
La pendiente m de una recta mide la inclinación de la siguiente manera:
•Si M>0 la función es creciente.
•Si M=0 la función es decreciente.
•Si M<0 la función es constante (recta horizontal).
La pendiente de una recta se puede hallar de la siguiente manera:
para lo cual es necesario disponer de dos puntos de la recta y hallar las variaciones
restando sus coordenadas x e y respectivamente.

23. Ejemplo:
Y=4x+2

24. Identidad
Una función identidad es una función matemática, de un conjunto M a sí mismo, que
devuelve su propio argumento.
f(x)=x / f(x)=y
La función identidad puede describirse de la forma siguiente:

25. Ejemplo: x 1 2 3 4
y 1 2 3 4
F(x)=x

26. Constante
Se llama función Polinómicas de grado cero o función matemática constante a la que no
depende de ninguna variable, se la representa de la forma:
F(x)= a
donde a es la constante.

27. Ejemplo:
Y= 5

28. Función
cuadrática
Una función cuadrática, es una función polinómica de grado par, que tiene como
máximo grado el numero 2. se define por la siguiente ecuación:
Para hallar el mínimo y máximo
Conjunto de salida: IR= dominio relativos, se usa la ecuación:
Conjunto de llegada= IR x= -b
2a
Rango= (máximos y mínimos de la función)
Punto de corte con y= c
Pun to de corte con x=

29. Función:

30. Función cúbica
Es una función polinómica de grado impar, cuyo grado mayor en el
termino de la ecuación es de 3.
Se da por la siguiente ecuación:
Conjunto de salida= IR=dominio
Conjunto de llegada= IR= rango
Punto de corte con y= d
Punto de corte con x=
factorizacion( teorema del factor)

31. Función=

32. Referencias de consulta
• http://es.wikipedia.org/wiki/Ecuación_de_tercer_gra
do
• http://es.wikipedia.org/wiki/Función_cuadrática
• http://es.wikipedia.org/wiki/Función_matemática
• http://dieumsnh.qfb.umich.mx/DIFERENCIAL/funcio
nes.htm
• http://elcentro.uniandes.edu.co/cr/mate/estructural
/libro/estructural/node29.html