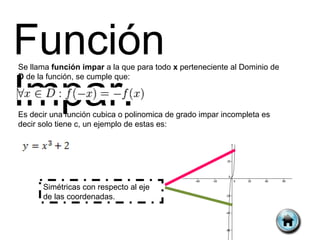
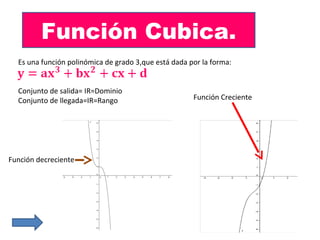
El documento presenta información sobre diferentes tipos de funciones matemáticas. Define qué es una función y explica conceptos como dominio, rango, puntos de corte, funciones inyectivas, biyectivas y sobreyectivas. Luego describe funciones particulares como funciones pares e impares, polinómicas, lineales, cuadráticas y cúbicas. Finalmente incluye referencias para consulta adicional.

1. Funciones.
Presentado por: Steffany Serebrenik, Hellen Kreinter y
David Castañeda.
Presentado a: Patricia Cáceres.
Colegio Colombo Hebreo
Grado Decimo.
Área de Matemáticas.

2. Funciones.
Generalidades.
Clases.
¿Qué es?
Representación.
Dominio, rango, puntos de
corte con x y con y.
Funciones: inyectivas,
biyectivas y sobreyectivas. .
Funciones pares
e impares.
Referencias de consulta.

3. ¿Qué es una función?
Una función, en matemáticas, es el término usado para indicar la relación o
correspondencia entre dos o más cantidades.
El término función fue usado por primera vez en 1637 por el matemático francés
René Descartes para designar una potencia x^n de la variable x.
Una función f de A en B es una relación que le hace corresponder a cada elemento “x” A
uno y solo un elemento “y” B, llamado imagen de x por f, que se escribe y=f (x).
Por tanto para ser función debe cumplir 2 condiciones:
a.Todo elemento del conjunto de partida A debe tener imagen.
b.Esta imagen debe ser única.
El conjunto formado por todos los
elementos de B que son imagen de algún
elemento del dominio se denomina
conjunto imagen o recorrido de f.

4. FORMAS DE REPRESENTAR UNA FUNCIÓN.
Verbal: como su mismo nombre lo Algebraica: A través de una
dice es con palabras. formula.
Ejemplo: Ejemplo:
P(t) es la población del mundo en X+25=y
el instante t.
Visual: Es decir a través de Numérica: Una herramienta para
diagramas y graficas. llevar a cabo esta es una tabla de
valores.
Ejemplo:
Onzas x 1 2 3 4 5 …
dólares y 11 12 13 14 15…

5. Rango: Es el conjunto formado por los valores que puede
llegar a tomar la función. Punto de corte con Y:
Para hallar el punto de corte
Sea f(x) : A B R= {y/y B y R x} con Y, se debe reemplazar en
la ecuación a X por 0.
El conjunto de llegada contiene los elementos que son la
imagen de los valores del conjunto de salida.
Dominio: Es el conjunto de existencia dela función, es decir, Punto de corte con X:
los valores para los cuales la función está definida. Es el
conjunto de todos los objetos que puede transformar. Para hallar el punto de corte
con x, se debe reemplazar en
la ecuación a Y por 0. (en un
Sea f(x) : A B R= {x/x x A^xRy y B} polinomio de grado mayor a
A
uno, se debe utilizar los
conjunto de salida se llama al conjunto que contiene los diferentes métodos de
elementos del dominio de una función. factorización.)

6. Este tipo de función cumple la condición de que a cada valor del conjunto A (dominio) le
corresponde un valor distinto en el conjunto B (imagen) de f . Es decir, a cada elemento
del conjunto A le corresponde un solo valor tal que, en el conjunto A no puede haber dos
o más elementos que tengan la misma imagen.
d
e
g
h

7. Este tipo de función se da cuando cada elemento de "Y" es la imagen de como mínimo
un elemento de "X".
d
e
g

8. Este tipo de función se da cuando es al mismo tiempo inyectiva y sobreyectiva. Para ser
más claro se dice que una función es biyectiva cuando todos los elementos del conjunto
de partida en este caso (x) tienen una imagen distinta en el conjunto de llegada, que es
la regla de la función inyectiva. sumándole que cada elemento del conjunto de salida le
corresponde un elemento del conjunto de llegada, en este caso (y) que es la norma que
exige la función sobreyectiva.
d
e
f
h

9. Función par.
El término función par suele referirse a una clase especial de funciones de
variable real: una función es una función par si para se
cumple la relación:
.
Es decir es una función cuadrática o polinomica de grado par incompleta que solo
tiene c , un ejemplo de estas es:
Simétricas con respecto al eje Y.

10. Función
Se llama función impar a la que para todo x perteneciente al Dominio de
Impar.
D de la función, se cumple que:
Es decir una función cubica o polinomica de grado impar incompleta es
decir solo tiene c, un ejemplo de estas es:
Simétricas con respecto al eje
de las coordenadas.

11. Exponencial
Racional Por Partes o a Trozos
Polinómica Valor Absoluto
Clases de funciones.
Trigonométricas Logarítmica

12. Función Polinomica.
Función de
Grado impar. Función de Constante.
Grado par.
Función
lineal. Función
Cuadrática.
Función
Cubica.

13. Funciones Polinómicas.
Son aquellas que surgen de evaluar los polinomios sobre las variables en las que están
definidos.
Dominio= Conjunto de Salida= R
Conjunto de llegada=R
Según el grado del polinomio las funciones Polinómicas pueden clasificarse en:
Grado Nombre Expresión
0 función constante y=a
y = ax + b es un
1 función lineal binomio del primer
grado
y = ax² + bx + c es
2 función cuadrática un trinomio del
segundo grado
Y=ax3+bx2+cx+d
3 función cúbica

14. Son funciones en las que el máximo grado de un término de la ecuación es un
número par. Está dada por la ecuación:
Conjunto de salida=Dominio=IR
Conjunto de llegada=IR Rango =(depende de los máximos y mínimos que tenga la
función)
Ejemplo :
Función cuadrática
Punto de corte con y= -1
Puntos de corte con x=(1,-1)
Vértice= (0,-1)
Conjunto de salida=Dominio=IR
Conjunto de llegada =IR Rango=(-1, ∞
)
F(x) ≥0 en x ( - ∞.-1) U (1, ∞)
F(x) ≤0 en x (-1,1)

15. Son funciones en las que el máximo grado de un término de la ecuación es un
número impar . Está dada por la ecuación:
Conjunto de salida=Dominio=IR
Conjunto de llegada=IR Rango =IR excepto en la lineal
constante.
Ejemplo :
Función cúbica
Punto de corte con y= 1
Punto de corte con x=-0.7
Conjunto de salida=Dominio=IR
Conjunto de llegada =IR= Rango
F(x) ≥0 en x ( -0.7, ∞) F(x) ≤ 0 en x (- ∞,-0.7)

16. Función lineal.
Lineal.
Generalidades.
Afín.
Idéntica.
Conclusiones.

17. Generalidades.
x-y son variables,
m se denomina pendiente e
indica el grado de inclinación de la
recta.
m se halla a través de la Dominio= Conjunto de Salida= R
expresión: Rango= R (a excepción de la constante).
Conjunto de llegada=R
CABE ANOTAR QUE:
Indica el punto de corte
si m > o: la función es creciente
con y Y por tanto el
si m < 0:la función es decreciente
desplazamiento vertical.
si m = 0 : la función es constante
La Función lineal es una
función polinomica.

18. Lineal.
La función lineal esta definida por la ecuación:
En esta función el punto de corte con x y con y son
respectivamente (0,0).
Dominio=Conjunto de salida= IR
Rango=Conjunto de llegada= IR

19. Afín.
La función Afín es un tipo de función lineal que tiene un desplazamiento
vertical, esta dada por la ecuación: EJEMPLO:
y=2x+3
Dominio= Conjunto de Salida= R
Rango=Conjunto de llegada=R
Punto de corte con y=n

20. Constante.
La función constante es un tipo de función lineal, en la que los elementos del
dominio se relacionan con los iguales en el conjunto de llegada. La podemos
representar como una función matemática de la forma:
donde a pertenece a los números reales.
•Dominio=Conjunto de Salida= IR
•Conjunto de llegada= IR
•Rango= {a}
•Punto de corte con Y= a.
Ejemplo:
Y= 3

21. Idéntica.
La función idéntica es una clase de función lineal donde a cada número del eje y le
corresponde el mismo número en el eje x, es decir, que las dos coordenadas de cada punto
son idénticas . EJEMPLOS:
Esta dada por la ecuación:
Rango = Conjunto de llegada = IR
Dominio= Conjunto de salida=IR

22. Conclusiones.
La principal diferencia entre función lineal y función lineal Afín, teniendo en
cuenta la ecuación general planteada en las generalidades es que la función
lineal desplazamiento vertical mientras que la otra si.
 La principal diferencia entre la función lineal y la función constante es que
esta última cumple la condición de que para todo elemento del dominio la
imagen es la misma.
 La principal diferencia entre la función lineal y la función lineal idéntica como
su mismo nombre lo dice hay una igualdad que se ve representada en que cada
elemento del dominio le corresponde la imagen de si mismo.

23. Función Cuadrática.
Es un tipo de función polinómica que
se define mediante un polinomio de
segundo grado
y se expresa como:
Máximo relativo.
Es una de las funciones mas estudiadas
en los diferentes campos, debido a sus Mínimo relativo.
propiedades simétricas y a su presencia
en la naturaleza. La grafica que forma se
le da el nombre de parábola y en ella hay
un eje de simetría y un mínimo o máximo
relativo lo que indica la parte mas baja o
alta a la que llega la parábola
respectivamente.
El rango es desde –oo(infinito) hasta el máximo
relativo si es decreciente o desde el mínimo
relativo, hasta oo si es creciente.
Para hallar el mínimo y máximo relativos, se usa la
ecuación:
x= -b
2a

24. Creciente: Si m( pendiente) es
positiva.
Decreciente: Si m( pendiente) es
negativa.
El punto de corte con y es c, mientras que
los puntos de corte con x o también Es importante recordar
llamados raíces se deben hallar que la parábola, formada
factorizando ya sea por los diferentes por la función cuadrática,
métodos o usando la siguiente formula tiene un eje de simetría, es
general: decir que si se divide
exactamente en dos, un
lado es el reflejo del otro
lado.

25. Función Cubica.
Es una función polinómica de grado 3,que está dada por la forma:
Conjunto de salida= IR=Dominio
Conjunto de llegada=IR=Rango Función Creciente
Función decreciente

26. Ejemplo:
Y= 3x3+4x2+3x-1
Conjunto de salida=Dominio= IR
Conjunto de llegada=Rango= IR
Punto de corte con x= 0.3
Punto de corte con y= -1
F(x) > 0 en x ∈ (0.3, infinito)
F(x) < 0 en x ∈ (0.3,-infinito)

27. Referencias de consulta.
http://es.wikipedia.org/wiki/Funci%C3%B3n_matem%C3%A1tica
http://es.answers.yahoo.com/question/index?qid=20080913105146AA0LLFk
http://es.wikipedia.org/wiki/Dominio_de_definici%C3%B3n
http://es.wikipedia.org/wiki/Rango
http://es.wikipedia.org/wiki/Funci%C3%B3n_inyectiva
http://www.amschool.edu.sv/paes/f10.htm
http://es.wikipedia.org/wiki/Funci%C3%B3n_biyectiva
http://www.disfrutalasmatematicas.com/conjuntos/inyectivo-sobreyectivo-biyectivo.html
http://es.wikipedia.org/wiki/Funci%C3%B3n_sobreyectiva
http://es.wikipedia.org/wiki/Funci%C3%B3n_par
http://es.wikipedia.org/wiki/Funci%C3%B3n_impar
http://www.educar.org/enlared/planes/paginas/funcionpar.htm
http://www.slideshare.net/mfatela/3-funcin-par-e-impar
http://es.wikipedia.org/wiki/Funci%C3%B3n_polin%C3%B3mica
http://www.hiru.com/es/matematika/matematika_03300.html
http://es.wikipedia.org/wiki/Funci%C3%B3n_lineal
http://www.x.edu.uy/lineal.htm
http://www.mitecnologico.com/Main/Funciones
http://analisismatematico.wordpress.com/2008/05/21/funcion-constante/
http://es.wikipedia.org/wiki/Funci%C3%B3n_cuadr%C3%A1tica
http://es.wikipedia.org/wiki/Ecuaci%C3%B3n_de_tercer_grado
Libro Precalculo, James Stewart, Sección de funciones( como representar).