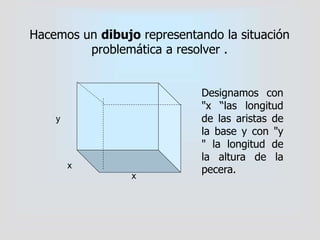
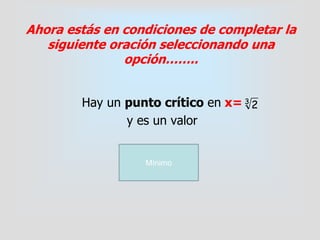
La pecera debe tener una capacidad de 1 m3. Se busca minimizar el costo de construcción, el cual depende de la cantidad de vidrio necesaria. El costo por metro cuadrado de vidrio es de $6. Se propone que la pecera tenga forma de prisma de base cuadrada. Se desarrolla una función para calcular el área total en términos de la longitud de un lado de la base x, y se encuentra que el área es mínima cuando x es igual a 3/2 metros.

1. Proponemos un problema para
aplicar lo aprendido:
Se desea construir una pecera con forma de
prisma de base cuadrada y
con una capacidad de 1 m3 de agua.
El vidrio con que se construirá cuesta $6 el m2.
¿Qué dimensiones de la pecera
hacen mínimo el costo?

2. Hacemos un dibujo representando la situación
problemática a resolver .
Designamos con
"x “las longitud
de las aristas de
la base y con "y
" la longitud de
la altura de la
pecera.
x
x
y

3. La función que se quiere minimizar es la función
costo, y ella está directamente relacionada con la
cantidad de vidrio necesario para la construcción
de la pecera.
¿Cuál de las siguientes funciones corresponde a la
función superficie del rectángulo?
A = 4. x.y + x2
V = x2.y = 1

4. La función que se quiere minimizar es la función costo, y
ella está directamente con la cantidad de vidrio necesario
para la construcción de la pecera.
Si seleccionaste la opción A = 4. x.y + x2
Estás en condiciones de
seguir avanzando….

5. Planteamos una ecuación que relacione las
distintas variables del problema:
Despejamos “y” de la ecuación del Volumen
y =
Sustituimos ahora en la función área :
A = 4. x. + x2
2
x
1
2
x
1

6. Resulta una función en una sóla variable:
A =
cuyo valor mínimo debemos encontrar.
¿Cuál es el Dominio de la función A(x)?
x >0 x  R
2
3
x
x4

7. Inténtalo de nuevo

8. Obtenemos la primera derivada de la
Función Area
Para determinar los valores críticos analizamos las dos
condiciones posibles:
 x/S´ (x) = 0
 x/no existe S´ (x)
A’(x) = 2
3
x
4-2x

9. Como pudiste comprobar, la función A´(x)
está definida en el mismo Dominio que
A(x), por lo tanto existe ∀ x>0 y
A´(x)=0 si x=
¿Eres capaz de analizar si este valor es máximo o mínimo?
3
2

10. Ahora estás en condiciones de completar la
siguiente oración seleccionando una
opción……..
Hay un punto crítico en x=
y es un valor
Mínimo
3
2

11. Vemos, que al pasar por x = , la función cambia de
decreciente a creciente, por lo tanto la misma presenta
en x = un mínimo local.
Si x = , resulta y = 3
4
1
3
2
3
2
Por lo tanto las dimensiones de la pecera para que el
costo de su construcción resulte mínimo son: m de
arista de la base y m de altura.
3
2
3
2
3
4
1