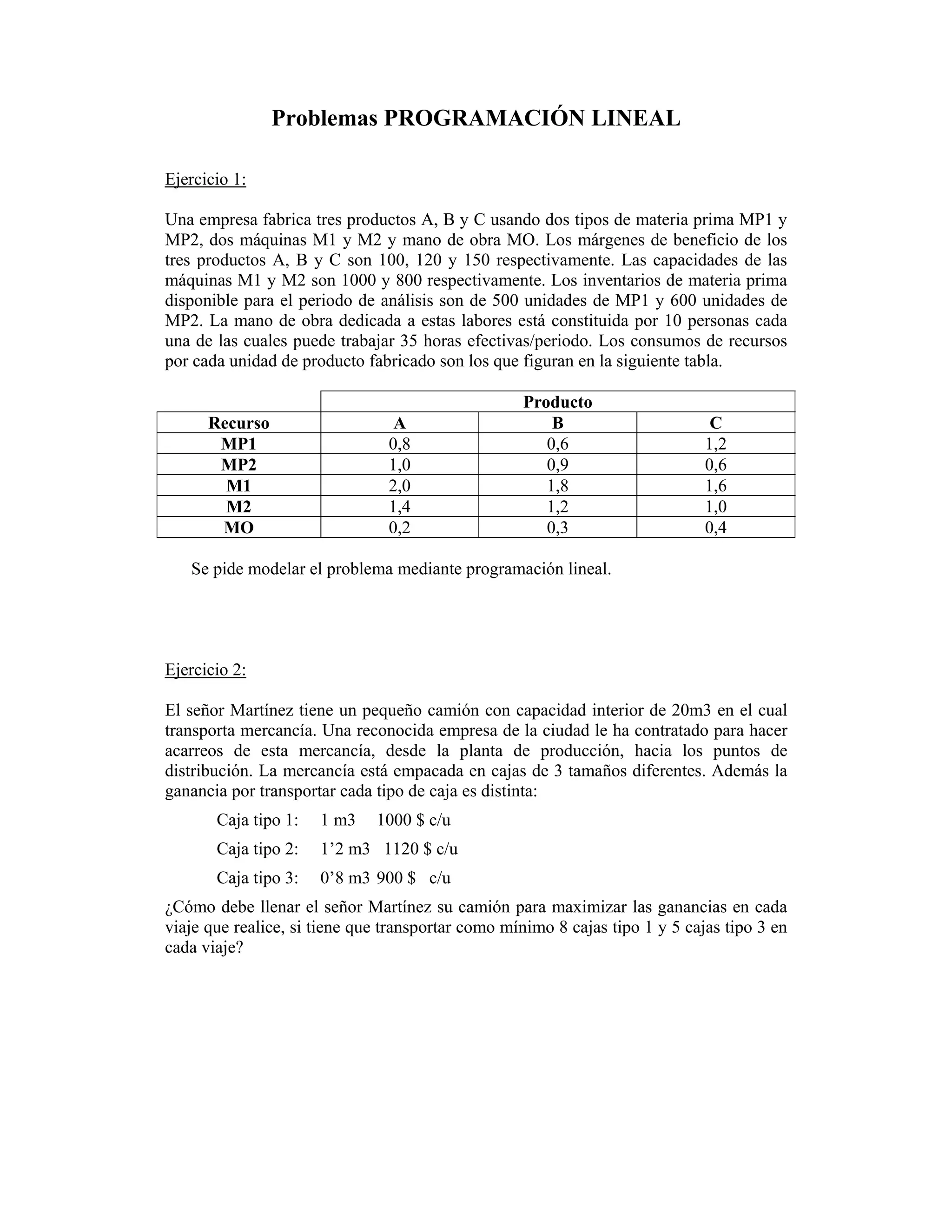
El documento presenta una serie de ejercicios de programación lineal en contextos de optimización de recursos en empresas y situaciones personales. Cada ejercicio aborda un problema específico, como la producción de bienes, la maximización de ganancias en transporte, o la planificación de dietas, estableciendo condiciones y requerimientos que deben ser satisfechos. Se solicita modelar cada situación mediante programación lineal para encontrar soluciones óptimas.

1. Problemas PROGRAMACIÓN LINEAL
Ejercicio 1:
Una empresa fabrica tres productos A, B y C usando dos tipos de materia prima MP1 y
MP2, dos máquinas M1 y M2 y mano de obra MO. Los márgenes de beneficio de los
tres productos A, B y C son 100, 120 y 150 respectivamente. Las capacidades de las
máquinas M1 y M2 son 1000 y 800 respectivamente. Los inventarios de materia prima
disponible para el periodo de análisis son de 500 unidades de MP1 y 600 unidades de
MP2. La mano de obra dedicada a estas labores está constituida por 10 personas cada
una de las cuales puede trabajar 35 horas efectivas/periodo. Los consumos de recursos
por cada unidad de producto fabricado son los que figuran en la siguiente tabla.
Producto
Recurso A B C
MP1 0,8 0,6 1,2
MP2 1,0 0,9 0,6
M1 2,0 1,8 1,6
M2 1,4 1,2 1,0
MO 0,2 0,3 0,4
Se pide modelar el problema mediante programación lineal.
Ejercicio 2:
El señor Martínez tiene un pequeño camión con capacidad interior de 20m3 en el cual
transporta mercancía. Una reconocida empresa de la ciudad le ha contratado para hacer
acarreos de esta mercancía, desde la planta de producción, hacia los puntos de
distribución. La mercancía está empacada en cajas de 3 tamaños diferentes. Además la
ganancia por transportar cada tipo de caja es distinta:
Caja tipo 1: 1 m3 1000 $ c/u
Caja tipo 2: 1’2 m3 1120 $ c/u
Caja tipo 3: 0’8 m3 900 $ c/u
¿Cómo debe llenar el señor Martínez su camión para maximizar las ganancias en cada
viaje que realice, si tiene que transportar como mínimo 8 cajas tipo 1 y 5 cajas tipo 3 en
cada viaje?

2. Ejercicio 3:
La señora María Eugenia, dietista del Hospital General, es la responsable de la
planificación y administración de los requerimientos alimenticios de los pacientes. En la
actualidad examina el caso de un paciente, a quien se le ha formulado una dieta especial
que consta de 2 fuentes alimenticias. Al paciente no se le ha restringido la cantidad de
alimentos que puede consumir; sin embargo, deben satisfacerse ciertos requerimientos
nutricionales mínimos por día.
Determinar la combinación de fuentes alimenticias que arroje el menor costo y satisfaga
todos los requerimientos nutritivos.
Ejercicio 4:
Una pequeña carpintería dispone de dos máquinas A y B para la fabricación de sillas y
mesas. Cada silla produce un beneficio de 10$ y cada mesa 30$. Cada silla requiere
cuatro horas en A y ocho en B, mientras que cada mesa precisa de seis horas en A y
cuatro en B. Durante la semana entrante las máquinas A y B tienen 12 y 16 horas
disponibles, como máximo respectivamente para estos trabajos. Suponiendo que existe
demanda para ambos productos, ¿cuántas sillas y mesas deben fabricarse para conseguir
un beneficio máximo?
Ejercicio 5:
Para la fiesta de su hijo, una ama de casa desea hacer unos pastelillos. Sus
conocimientos culinarios le permiten hacerlos de tres tipos A, B y C, en todos los cuales
intervienen como ingredientes mantequilla, nata y crema, de los que posee 232, 300 y
720 gramos, respectivamente.
Un pastelillo del tipo A precisa 5 gramos de mantequilla, 8 de nata y 9 de crema. Uno
de tipo B, 6, 5 y 8 respectivamente y uno de tipo C 4 de mantequilla, 6 de nata y 12 de
crema. La madre sospecha que le resultará preferible optimizar la cantidad de pastelillos
a hacer antes que cualquier otra consideración. En consecuencia, ¿cuál es el número
óptimo de pastelillos a fabricar?

3. Ejercicio 6:
Supongamos un fabricante que tiene dos recursos primarios de fabricación: tiempo -
máquina y horas de trabajo. Durante cierto período de producción, dispone de 200 horas
– máquina y 300 horas de trabajo para dedicarlas a tres productos. El producto 1
necesita 15 horas – máquina y 10 horas de trabajo por unidad. El producto 2 requiere 10
horas – máquina y 25 horas de trabajo por unidad. Finalmente el producto 3 necesita 10
horas – máquina y 20 horas de trabajo por unidad.
El fabricante desea determinar el conjunto de productos que harán máximo su beneficio,
sin que se exceda del total de horas –máquina disponibles. Desea también obtener un
completo empleo de sus obreros (que todas las horas-hombre que dispone sean
utilizadas). Los beneficios del fabricante serán de 5$ por unidad de producto 1, 10$ por
unidad de producto 2 y 12$ por unidad de producto 3.
Ejercicio 7:
Disponemos de 210.000 euros para invertir en bolsa. Nos recomiendan dos tipos de
acciones. Las del tipo A, que rinden el 10% y las del tipo B, que rinden el 8%.
Decidimos invertir un máximo de 130.000 euros en las del tipo A y como mínimo
60.000 en las del tipo B. Además queremos que la inversión en las del tipo A sea menor
que el doble de la inversión en B. ¿Cuál tiene que ser la distribución de la inversión para
obtener el máximo interés anual?
Ejercicio 8:
Una empresa puede elaborar dos tipos de tejido: tipo I y tipo II. Las necesidades de
horas/máquina, por cada metro de tejido, son de 3 horas el primero y 4 horas el
segundo. El tipo I requiere 2 horas/hombre por cada metro, mientras que el tipo II
precisa, también por cada metro de tejido, 6 horas/hombre. Además, dada las
limitaciones de la demanda, no se venderían más de 30 metros del tejido tipo I, cada
quincena, por lo que no se desea superar ese nivel de producción. Se dispone de 120
horas/hombre y 120 horas/máquina cada 15 días y el margen de beneficio de cada metro
de tejido es de 220 $ en el tipo I y de 140 $ en el tipo II. Se pide:
a) Plantear el modelo de programación lineal para maximizar el beneficio de la
empresa.
b) Represente la región factible de soluciones.
c) Resolución gráfica.
d) Determinar los metros de tejido de cada tipo que hay que elaborar, cada 15 días,
para maximizar el beneficio de la empresa.
e) Calcular el máximo beneficio quincenal que puede conseguirse.

4. Ejercicio 9:
Ejercicio 10: