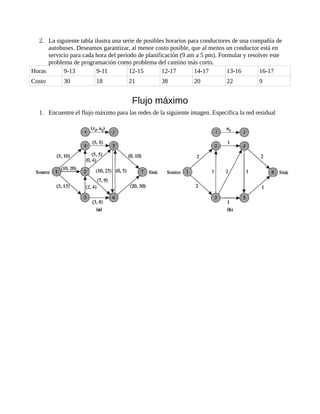
Este documento presenta tres algoritmos de optimización en grafos: el algoritmo de Kruskal para encontrar el árbol de expansión mínima, el algoritmo de Dijkstra para encontrar el camino más corto y el algoritmo de flujo máximo para encontrar el flujo máximo en una red. Instruye al lector en cómo aplicar estos algoritmos para resolver problemas de ruta óptima, programación y flujo en redes.

1. Arbol de expansión mínima
1. Utiliza el algoritmo de Kruskal para encontrar el arbol de expansión mínima en las siguientes
figuras
2. Piensa que la red de la siguiente figura como un mapa de autopista y los números asociados a
los arcos son las elevaciones de cada uno de los caminos. Un viajero planea manejar del nodo 1
hasta el nodo 12. El viajero no puede viajar por zonas tan elevadas por cuestiones de salud y
desearía encontrar el mejor camino para llegar a su destino en base a su condición para viajar.
Ayudale a encontrarlo mediante el arbol de expansión mínima.
Camino más corto
1. Resuelve el problema del camino más corto en las figuras siguientes usando el algoritmo de
Dijkstra.

2. 2. La siguiente tabla ilustra una serie de posibles horarios para conductores de una compañía de
autobuses. Deseamos garantizar, al menor costo posible, que al menos un conductor está en
servicio para cada hora del período de planificación (9 am a 5 pm). Formular y resolver este
problema de programación como problema del camino más corto.
Horas 9-13 9-11 12-15 12-17 14-17 13-16 16-17
Costo 30 18 21 38 20 22 9
Flujo máximo
1. Encuentre el flujo máximo para las redes de la siguiente imagen. Especifica la red residual