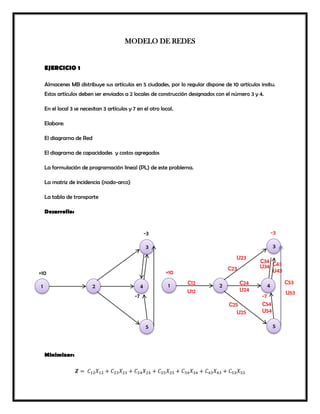
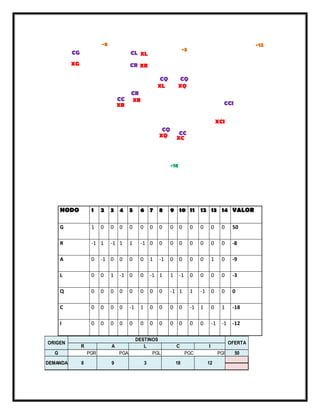
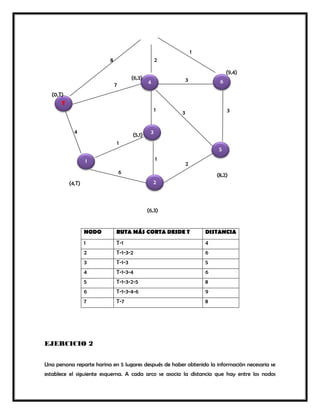
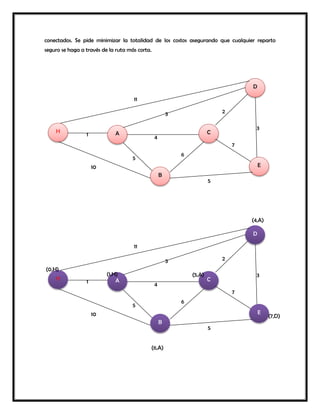
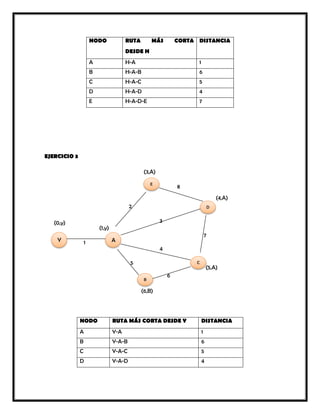
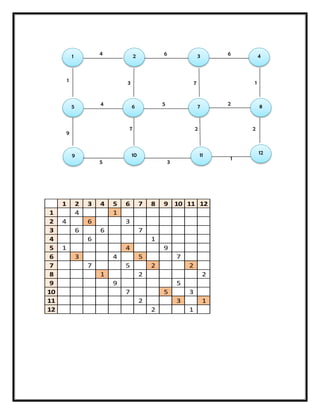
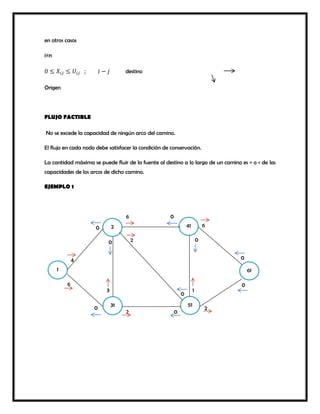
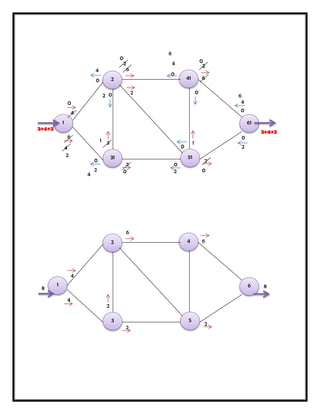
Este documento presenta varios modelos y algoritmos para resolver problemas de optimización en redes, incluyendo modelos de redes de transporte, el problema de la ruta más corta, el árbol de expansión mínimo y el flujo máximo. Explica los pasos para formular y resolver cada problema matemáticamente usando programación lineal u otros métodos como el algoritmo glotón. También incluye ejemplos numéricos para ilustrar cada modelo.

1. UNIDAD III
MODELO DE REDES Y ADMINISTRACIÓN DE
PROYECTOS

2. MODELO DE REDES
EJERCICIO 1
Almacenes MB distribuye sus artículos en 5 ciudades, por lo regular dispone de 10 artículos insitu.
Estos artículos deben ser enviados a 2 locales de construcción designados con el número 3 y 4.
En el local 3 se necesitan 3 artículos y 7 en el otro local.
Elabore:
El diagrama de Red
El diagrama de capacidades y costos agregados
La formulación de programación lineal (PL) de este problema.
La matriz de incidencia (nodo-arco)
La tabla de transporte
Desarrollo:
Minimizar:
𝒁 = 𝐶12 𝑋12 + 𝐶23 𝑋23 + 𝐶24 𝑋24 + 𝐶25 𝑋25 + 𝐶34 𝑋34 + 𝐶43 𝑋43 + 𝐶53 𝑋53
+10
1 2
5
4
3
-3
-7
C54
C43
C12
C25
C24
C23
+10
1 2
5
4
3
-3
-7
U12
U23
U24
U25
U53
C53
C34
U34
U43
U54

3. 𝑋12 = 10
-𝑋12 + 𝑋23 + 𝑋24 + 𝑋25 = 0
−𝑋23 + 𝑋34 − 𝑋43 − 𝑋53 = −3
−𝑋24 − 𝑋34 + 𝑋43 − 𝑋54 = −7
−𝑋25 + 𝑋53 + 𝑋54 = 0
Matriz de incidencia
Tabla de Transporte
𝒁 = 𝟑𝑷𝟏𝟑 + 𝟕𝑷𝟏𝟒
EJEMPLO 2
NODO (1,2) (2,3) (2,4) (2,5) (3,4) (4,3) (5,3) (5,4) VALOR
1 1 0 0 0 0 0 0 0 10
2 -1 1 1 1 0 0 0 0 0
3 0 -1 0 0 1 -1 -1 0 -3
4 0 0 -1 0 -1 1 0 -1 -7
5 0 0 0 -1 0 0 1 1 0
Sumas 0 0 0 0 0 0 0 0 0
ARCOS
3 4 OFERTA
O
R
I
G
E
N
1 P13 P14 10
DEMANDA 3 7
DESTINO
A
LRG I
CR
A CA
L
CL
A
CAI
XR
A
XA
L
XL
A
XAI
50
-9

4. NODO 1 2 3 4 5 6 7 8 9 10 11 12 13 14 VALOR
G 1 0 0 0 0 0 0 0 0 0 0 0 0 0 50
R -1 1 -1 1 1 -1 0 0 0 0 0 0 0 0 -8
A 0 -1 0 0 0 0 1 -1 0 0 0 0 1 0 -9
L 0 0 1 -1 0 0 -1 1 1 -1 0 0 0 0 -3
Q 0 0 0 0 0 0 0 0 -1 1 1 -1 0 0 0
C 0 0 0 0 -1 1 0 0 0 0 -1 1 0 1 -18
I 0 0 0 0 0 0 0 0 0 0 0 0 -1 -1 -12
G PGR PGA PGL PGC PGI 50
18
R A L I
DEMANDA 8 9 3 12
C
ORIGEN
DESTINOS
OFERTA
CG
R
CL
R
CR
L
CQ
L
CQ
L
CCI
CC
Q
CQ
C
CR
CCC
R
XG
R
XCI
XQ
L
XL
Q
XL
R
XR
L
XR
C
XR
C
XQ
C
XC
Q
-8
-3
-12
-18

5. 𝒁 = 𝟖𝑷𝑮𝑹 + 𝟗𝑷𝑮𝑨 + 𝟑𝑷𝑮𝑳 + 𝟏𝟖𝑷𝑮𝑪 + 𝟏𝟐𝑷𝑮𝑰
EL PROBLEMA DE LA RUTA MÁS CORTA
Se refiere a una red en la que cada arco (i,j) tiene asociado un número Cij que se interpreta
como la distancia (Costo, Tiempo) que hay entre los NODOS i,j. El objetivo consiste en encontrar
las rutas más cortas (económicas, rápidas) entre un nodo específico y todos los demás nodos de la
red.
ALGORITMO
PASO 1
Considere todos los nodos que estén directamente conectados con el origen, el componente de
distancia de la etiqueta que se pone a cada nodo es la distancia desde el origen, el componente
predecesor es el origen. Estas etiquetas se llaman temporales.
PASO 2
De entre todos los nodos con etiqueta temporal escoja uno cuyo componente de distancia sea
mínima y etiquételo permanentemente.
Todos los empates en cualquier punto del algoritmo se rompen arbitrariamente. Tan pronto
como todos los nodos han sido etiquetados en forma permanente vaya al paso 4.
PASO 3
Todo nodo que no tenga etiqueta permanente no tiene etiqueta o su etiqueta es temporal.
Considérese todas las etiquetas de los vecinos del nodo, para cada uno de estos nodos calcular la
suma de su distancia más la componente de la distancia de la etiqueta.
Si el nodo no está etiquetado asigne una etiqueta temporal que consta de esta distancia y la del
predecesor.
Si el nodo en cuestión ya tiene etiqueta temporal, cambie si y solo si la distancia recién calculada
es menor que la distancia de la etiqueta actual y regrese al paso dos.

6. PASO 4
Las etiquetas permanentes indican la distancia más corta desde el origen a cada nodo de la red
también indican el nodo predecesor en la ruta más corta hacia cada nodo.
EJERCICIO 1
Una persona hace frecuentes repartos de cerveza a 7 sectores diferentes de Riobamba. Después
de haber obtenido la información necesaria se establece el siguiente esquema a cada arco se
asocia la distancia que hay entre los nodos conectados se piensa minimizar la totalidad de sus
costos asegurando que cualquier reparto futuro se haga a través de la ruta más corta.
Se debe resolver en (n-1) pasos. (8-1)=7 pasos
7
4 6
5
3
2
1
T
1
3
3
2
3
1
1
1
2
7
1
1
8
4
6
1
7
(8,4)

7. NODO RUTA MÁS CORTA DESDE T DISTANCIA
1 T-1 4
2 T-1-3-2 6
3 T-1-3 5
4 T-1-3-4 6
5 T-1-3-2-5 8
6 T-1-3-4-6 9
7 T-7 8
EJERCICIO 2
Una persona reparte harina en 5 lugares después de haber obtenido la información necesaria se
establece el siguiente esquema. A cada arco se asocia la distancia que hay entre los nodos
4 6
5
3
2
1
T
1
3
3
2
3
1
1
1
2
7
1
1
8
4
6
1
(0,T)
(4,T)
(5,1)
(6,3)
(6,3)
(8,2)
(9,4)

8. conectados. Se pide minimizar la totalidad de los costos asegurando que cualquier reparto
seguro se haga a través de la ruta más corta.
H
E
D
C
B
A
11
3
6
7
5
23
4
5
10
1
H
E
D
C
B
A
11
3
6
7
5
23
4
5
10
1
(0,H)
(1,H) (5,A)
(4,A)
(6,A)
(7,D)

9. NODO RUTA MÁS CORTA
DESDE H
DISTANCIA
A H-A 1
B H-A-B 6
C H-A-C 5
D H-A-D 4
E H-A-D-E 7
EJERCICIO 3
NODO RUTA MÁS CORTA DESDE Y DISTANCIA
A Y-A 1
B Y-A-B 6
C Y-A-C 5
D Y-A-D 4
Y
C
D
E
B
A
(0,y)
(1,y)
(3,A)
(4,A)
(5,A)
(6,B)
1
2
3
7
4
5
6
8

10. E Y-A-E 3
PROBLEMA DEL ÁRBOL EXÁNDIDO MÍNIMO (ENLACES DE COMUNICACIÓN)
La tarea consiste en construir un árbol que conecte todos los NODOS de la red con un costo total
mínimo. Esto se conoce como árbol expandido mínimo o árbol de expansión mínima como
sabemos un árbol es el conjunto n-1 arcos (pasos) en una red de nodos en una red con n nodos
que conecte todo par de nodos.
ALGORITMO GLOTÓN
Este algoritmo resuelve el problema en un extremo simple, existen 2 formas que son:
El Método Gráfico
El Método Tabular
Método Gráfico
Comience en cualquier nodo, escoja el arco más barato que parta de cada nodo, este es su
primer enlace y se conoce como segmento de conexión entre dos nodos, los demás nodos se
llaman nodos desconectados.
Considere todos los arcos que parten del segmento de conexión a los nodos a los nodos
desconectados. Seleccione el más económico como siguiente enlace. Rompa arbitrariamente los
empates, esto agrega un nuevo nodo al segmento de conexión Repita este paso hasta que todos
los nodos estén conectados, es decir, requiere de n-1 pasos.
Método Tabular
Empiece arbitrariamente con cualquier nodo, se designa este nodo como conectado y coloque un
visto a lado de la fila correspondiente a este nodo y tache el índice de la columna que
corresponde a este.
Considere todas las filas que tenga el visto, busque el valor mínimo en las columnas cuyo índice
no han sido tachados y encierre ese valor en un círculo. Si existe empates rompa
arbitrariamente, la columna que tenga ese elemento encerrados en un círculo designe al nuevo

11. nodo conectado. Se tacha el índice de la columna y coloque una marca en el renglón
correspondiente a este nodo. Repita este paso hasta cuando todos los nodos estén conectados.
Una vez que todos los nodos hayan sido conectados identifique el árbol de expansión mínima
mediante los elementos encerrados en el círculo.
Se llama algoritmo glotón debido a que en cada paso se hace la mejor elección posible. Este es
uno de los pocos problemas de la ciencia administrativa donde se garantiza que el algoritmo
glotón nos dará la solución óptima.
EJERCICIO:
Se desea instalar una red de comunicación entre 12 ciudades, los costos entre pares permisibles
directos aparecen en el siguiente diagrama, cada unidad de costo representa $1000.00.
Recuerde la red identifica enlaces directos posibles.
Para este ejemplo se ha empezado en el NODO 1:
1 2
2
6
1211710
9
5 7 8
5
5
3
3
4
4
4
6 6
4 5 2
5
5
3 1
1
9
3
7
7
2
1
2

12. 1 2 3 4 5 6 7 8 9 10 11 12
1 4 1
2 4 6 3
3 6 6 7
4 6 1
5 1 4 9
6 3 4 5 7
7 7 5 2 2
8 1 2 2
9 9 5
10 7 5 3
11 2 3 1
12 2 1
1
1211109
5 6 7 8
2 3 44 6 6
1
9
5
4
3
25
7 1
2
3
7
1
2

13. FLUJO MÁXIMO
Aquí encontramos un solo nodo fuente (un solo nodo de entrada) y un solo nodo destino (un solo
nodo de salida) el objetivo consiste en encontrar la máxima cantidad de flujo total (petróleo,
agua, mensajes, tránsito) que puede circular a través de la red en una unidad de tiempo.
La cantidad de flujo por unidad de tiempo en cada arco está limitado por las restricciones de
capacidad por ejemplo el diámetro del oleoducto del petróleo, el púnico requerimiento es que
para cada nodo se cumpla la siguiente relación:
Flujo que sale del nodo=flujo que entra al nodo.
En términos formales siendo 1 la fuente y m el destino debe cumplirse lo siguiente:
MAX f
∑ 𝑋𝑖𝑗 − 𝑋𝑖𝑗 = −𝑓; 𝑖 = 𝑛
1
1211109
5 6 7 8
2 3 46
1
5
4
3
25
1
3 1
2

14. en otros casos
i≠n
0 ≤ 𝑋𝑖𝑗 ≤ 𝑈𝑖𝑗 ; 𝑖 − 𝑗 destino
Origen
FLUJO FACTIBLE
No se excede la capacidad de ningún arco del camino.
El flujo en cada nodo debe satisfacer la condición de conservación.
La cantidad máxima se puede fluir de la fuente al destino a lo largo de un camino es = o < de las
capacidades de los arcos de dicho camino.
EJEMPLO 1
1
5131
412
61
6 0
0
20
4
R
6
3
0
2 0
2
0
6
0
0
1
0

15. 1
5131
412
61
6
0
0
20
4
R
6
3
0
2 0
2
0
6
0
0
1
0
2+4+2
2+4+2
4
2 0 2 0
2
0
4
2 4
4
2
2
1
0 0
6
6
2
0
0
4
1
53
42
6
6
4
R
4
2
2
2
6
8 8