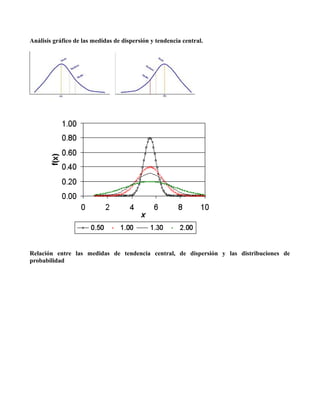
Este documento presenta un resumen de las primeras tres sesiones de un curso sobre teoría de la probabilidad y estadística. La primera sesión introduce la teoría de conjuntos. La segunda sesión cubre conceptos básicos de estadística como población, muestra, variables y medidas de tendencia central y dispersión. La tercera sesión introduce conceptos básicos de teoría de probabilidad como experimentos aleatorios, eventos y espacios de muestreo.

1. SESIÓN 1: TEORÍA DE CONJUNTOS
Lunes 6 de Febrero/2012
Introducción al curso:
− Probabilidad, estadística, teorías de la confiabilidad, de colas y de muestreo para calidad,
procesos estocásticos
− Programa del curso:
1. Introducción: teoría de conjuntos, estadística y probabilidad.
2. Teoría de la probabilidad
3. Variables aleatorias
4. Esperanza matemática
5. Distribuciones de probabilidad
6. Teorías de la confiabilidad y de colas
7. Procesos estocásticos
− Metodología de evaluación:
Talleres y parciales
2 talleres de 7,5%, parcial 1 de 15%, 2 talleres de 7,5%, parcial 2 de 15% y examen final de 40%.
− Aulas virtuales
Bibliografía:
Probabilidad y Estadística para ingenieros - Ronald Walpole
Estadística y muestreo – Ciro Martinez Bencardino
Estadística – Murray Spiegel (Serie SHAUM)
Teoría de conjuntos y temas afines – Lipschutz Seymour (Serie SCHAUM)
Carlos Ivorra Castillo – Lógica y teoría de conjuntos, Capitulo X (Visión axiomática)
Links recomendados:
http://www.uv.es/ivorra/Libros/Logica.pdf
1. Definición de conjunto y elemento (concepto primitivo que implica axiomas)
Colección, agrupación o lista de elementos. Los conjuntos pueden ser finitos (el número de elementos
será su cardinal) o infinitos.
Cuál es la diferencia entre un conjunto, una serie y una sucesión?
Sucesión son elementos que pueden no tener una propiedad común.
Serie matemática: generalización de suma a elementos infinitos.
Los elementos definen el conjunto, no importa el orden, ningún elemento puede repetirse siendo está
una gran diferencia con una sucesión o una serie.
Elemento: es un objeto que es considerado una unidad en sí. Generalmente existe una (o varias)
propiedad común a todos los elementos de un conjunto.
Ejemplos:
El conjunto de los números reales
{Bogotá, Calí, Medellin}
Las resistencias en una tarjeta electrónica

2. Los abonados a una empresa de telefonía
Los conjuntos pueden definirse por comprensión mediante la definición de una o varias propiedades
comunes.
{x/x es una ciudad colombiana con más de 3 millones de habitantes}
Los conjuntos pueden definirse por extensión que es listarlos.
{Bogotá, Calí, Medellin}
Un método gráfico (no el único) de representar un conjunto es el diagrama de Venn.
Cómo se hace una representación en diagramas de Venn de conjuntos infinitos??
la representación de conjuntos infinitos o no bien definidos se realiza mediante áreas.
Formalmente se utiliza el concepto de función de pertenencia (a ∈ A) para indicar que un elemento
hace parte de un conjunto. En la lógica y teoría clásica de conjuntos se dice que si un elemento
pertenece a un conjunto su función de pertenencia es 1 y será 0 si no pertenece a dicho conjunto.
Qué pasa si la función de pertenencia no es 0 ni 1??
En la lógica difusa se trabaja con funciones de pertenencia cuyo valor puede ser un número real entre 0
y 1.
Qué es un multiconjunto??
En un multiconjunto un elemento puede repetirse varias veces lo que da origen al concepto de
multiplicidad que es aplicado en la programación orientada a objetos.
Definición de subconjunto
Un conjunto A es subconjunto de un conjunto B si cada elemento del conjunto A es parte del conjunto
B. Se dice que A es un subconjunto propio de B si no todos los elementos del conjunto B son parte del
conjunto A, osea si A y B son diferentes. También se dice que A está contenido en B. A ⊆ B.
La relación inversa a subconjunto es el superconjunto B ⊇ A.
En la teoría numérica, que conjuntos de números son subconjuntos de otros?
N (naturales) ⊆ Z (enteros) ⊆ Q (racionales) ⊆ R(reales) ⊆ I (imaginarios)
Igualdad de conjuntos:
Si 2 conjuntos contienen los mismos elementos se dice que son iguales.
2. Conjuntos universal y vacío
El conjunto vacío ∅ es aquel conjunto que no contiene ningún elemento.
El conjunto universal o referencial (U) es aquel conjunto del cuál todos los otros conjuntos tratados son
subconjuntos.
3. Operaciones entre conjuntos
Unión: Se define la operación unión de dos conjuntos A y B (A ∪ B) como el conjunto conformado por
los elementos que pertenecen a A, a B o a ambos.
Intersección: Se define la operación intersección de dos conjuntos A y B (A ∩ B) como el conjunto
conformado por los elementos que pertenecen simultaneamenta a A y a B.

3. Diferencia: Se define la operación diferencia de dos conjuntos A y B (A – B) como el conjunto
conformado por los elementos que pertenecen a A pero no a B.
Complemento: Se define la operación complemento del conjunto A (A') como el conjunto conformado
por los elementos del conjunto universal que no son parte del conjunto A (U – A).
Diferencia simétrica: Es el conjunto de elementos que pertenecen a A y a B pero no a los dos
simultaneamente.
Producto cartesiano: Se define el producto cartesiano entre los conjuntos A y B como el conjunto de
todos los pares (am, bn) donde am es elemento del conjunto A y bn es un elemento del conjunto B.
4. Álgebra de conjuntos
Asociatividad: A ∪ B ∪ C = (A ∪ B) ∪ C, A ∩ B ∩ C = (A ∩ B) ∩ C
Conmutatividad: A ∪ B = B ∪ A, A ∩ B = B ∩ A
Distributividad: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Absorciòn: A ∪ (A ∩ B) = A, A ∩ (A ∪ B) = A
Idempotencia: A ∪ A = A, A ∩ A = A
Identidad: A ∪ ∅ = A, A ∩ ∅ = ∅ Α ∪ U = U, Α ∩ U = A
Complemento: A ∪ A' = U, A ∩ A' = ∅, (A')' = A, U' = ∅
Leyes de Morgan:
A – B = A ∩ B'
Ejemplos:
• Demuestre (A – B) ∩ B = ∅
• Demuestre (A ∪ A) ∩ (A ∪ B`) = A

4. SESIÓN 2. FUNDAMENTOS DE ESTADÍSTICA
Martes 7 de Febrero/2012
Estadística: es el método científico de operar con un conjunto de datos y de interpretarlos.
Estadística descriptiva: trabaja los aspectos característicos de un conjunto de datos.
Inferencia estadística: deducción de información superior a partir de muestras.
Población: conjunto de objetos o individuos que comparten una característica común.
Muestra: conjunto de elementos extraídos de la población.
Unidad estadística: elemento de la población que reporta información.
Cuál es subconjunto de cuál??
La muestra es un subconjunto de la población. La unidad estadística es análoga a un elemento.
Datos: características o valores susceptibles de ser observados.
Variable: característica susceptible de tener diversos valores.
Parámetro: valores que caracterizan a la población (media, varianza)
Estadístico: valor que caracteriza a una muestra (media muestral, varianza muestral)
Aleatoriedad: una muestra debe ser escogida a la zar.
Representatividad: una muestra debe estar formada por un número razonable de elementos.
Tipos de muestra aleatoria:
Muestra aleatoria simple
Muestra aleatoria sistemática
Muestra aleatoria estratificada
Muestra aleatoria de conglomerados
Variables estadísticas:
Característica de una población que va a ser estudiada; puede ser cualitativa o cuantitativa (continua y
discreta).
Tabla (distribución) de frecuencias:
Es un resumen de datos en el cuál cada valor de la variable de muestreo se asocia con el número de
ocurrencias.
Existen diversas representaciones gráficas como las barras y los pasteles.
Para que la distribución de frecuencias no se vuelva engorrosa se maneja la distribución agrupada de
frecuencias en la cuál varias características son agrupadas en clases y cuyo valor medio se denomina
marca de clase.
Frecuencia absoluta: es el número de ocurrencias en la distribución de frecuencias de una característica.
Frecuencia relativa: es el cociente resultante entre la frecuencia absoluta y el número total de
ocurrencias; su valor estará entre 0 y 1.

5. Medidas de tendencia central:
Son medidas que resumen en un sólo número cierta descripción de un grupo:
Media aritmética:
Media ponderada:
Media geométrica:
Media armónica:
Mediana:
Moda:
Tendencia central:
Media aritmética: es la sumatoria de todos los datos obtenidos divida entre el número de datos.
Mediana (Me): es el valor que divide la distribución de datos ordenados en 2 mitades.
Moda (Mo): es el valor que más se repite dentro de una distribución de datos.
Media geometrica , media armónica. Deciles (se divide la muestra en 10), cuartiles, etc.
Ejemplo:
10 resistencias de ¼ de W y de igual valor han sido sometidas a varias corrientes hasta que se
quemaran; los tiempos medidos en segundos en que cada resistencia se quemo fueron:
5, 3, 6, 6, 5, 7, 6, 7, 7, 6
a. Realizar una tabla de distribución de frecuencias
b. Obtener la media aritmética, la moda y la mediana.
Medidas de dispersión:
Son medidas que indican que tan centrados está un conjunto de valores respecto a un valor central osea
que tanta variabilidad se tiene.
Varianza:
Desviación estándar: es una medida de la desviación de todos los valores respecto a la media.
s
Coeficiente de variación: es el cociente en porcentaje de la desviación estándar y la media aritmética.
Si es muy alto puede incluso decirse que los datos no son representativos.
CV = desviación estándar/promedio X100%

6. Análisis gráfico de las medidas de dispersión y tendencia central.
Relación entre las medidas de tendencia central, de dispersión y las distribuciones de
probabilidad

7. SESIÓN 3: INTRODUCCIÓN A LA TEORÍA DE LA PROBABILIDAD
Lunes 13 de Febrero/12
La teoría de la probabilidad incluye las teorías y fundamentos matemáticos para investigar fenómenos
aleatorios. El propósito de la teoría de la probabilidad es describir y predecir las tendencias de estos
fenómenos que ocurren en relación con experimentos aleatorios.
Experimento aleatorio:
1. Repeticiones del evento bajo las mismas condiciones generan salidas diferentes.
2. La posibles salidas generadas son conocidas.
− Número de vehículos que llegan a una estación de gasolina
− Número de estrellas visibles durante la noche
− Fluctuación de precios
Evento aleatorio simple o elemento: Posible resultado de un evento aleatorio.
Espacio de eventos o de muestreo: El conjunto de todos los posibles eventos simples; se denota como
M.
− Cuando una persona dice un número al azar
Espacio discreto de muestreo: Un espacio M es discreto si está conformado por un número finito de
elementos o un número infinito contable de eventos.
− Cuando se lanza un dado
Operaciones:
Unión: Sean A y B dos eventos aleatorios dentro del espacio de muestreo M entonces la operación A ∪
B se define como el evento de que ocurra A u ocurra B o ambos.
Intersección Sean A y B dos eventos aleatorios dentro del espacio de muestreo M entonces la
operación A ∩ B se define como el evento de que ocurran ambos A y B. 2 conjuntos son mutuamente
excluyentes si su intersección da como resultado el conjunto vacío.
Si A ⊆ B entonces la ocurrencia de A implica la ocurrencia de B.
AB corresponde al evento de que ocurra A pero no ocurra B.
A' = MA corresponde al evento de que ocurra M pero no A; se denomina el complemento de A,
Reglas de Morgan
Sea A1, A2, A3, … An una secuencia de eventos aleatorios, entonces:
Son las leyes de Morgan de la teoría lógica matemática aplicada a la teoría de la probabilidad.
Ejemplo: Para n = 2 se tiene
Tabla (distribución) de frecuencias y frecuencia relativa:

8. Es un resumen de datos en el cuál cada valor de la variable de muestreo se asocia con el número de
ocurrencias.
Existen diversas representaciones gráficas como las barras y los pasteles.
Para que la distribución de frecuencias no se vuelva engorrosa se maneja la distribución agrupada de
frecuencias en la cuál varias características son agrupadas en clases y cuyo valor medio se denomina
marca de clase.
Frecuencia absoluta: es el número de ocurrencias en la distribución de frecuencias de una característica.
Frecuencia relativa: es el cociente resultante entre la frecuencia absoluta y el número total de
ocurrencias; su valor estará entre 0 y 1.
Probabilidad
Siendo A un conjunto de elementos de M, se define la función de probabilidad del evento A como P(A)
con las siguientes condiciones:
1. P(M) = 1, P(∅) =0
2. Para cualquier evento A, 0 ≤ P(A) ≤ 1
3. Para cualquier secuencia de eventos mutuamente excluyentes (conjuntos disyuntos)
Para estimar la probabilidad de un evento se parte de la frecuencia relativa de dicho evento; en general
se aplica la siguiente fórmula:
Con N siendo el número total de muestras, N(A) el número de veces que se repite el evento A y N(A)/N
la frecuencia relativa. En el caso de un espacio muestral discreto se obvia el límite.
Propiedades de la función de probabilidad:
1.
2. Para dos eventos A y B, P(BA) = P(B) – P(A ∩ B)
En particular si A ⊆ B entonces P(BA) = P(B) – P(A), P(A) < P(B)
3. P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
En particular si A y B son dos eventos excluyentes P(A ∪ B) = P(A) + P(B)
Ejemplo 1:
Cuál es la probabilidad de que una moneda caiga con el costado de sello hacia arriba al lanzarla?
/Solución
El conjunto universal de eventos U o espacio M está compuesto por los eventos “Cara” y “Sello”.
El número posible de resultados es 2 (cara y sello); la probabilidad de que ocurra “Sello” es igual al
número de elementos en el conjunto “Sello” dividido en el número de elementos del conjunto M osea
½.

9. SESIÓN 4: TALLER No. 1 – BASES DE CONJUNTOS, ESTADÍSTICA Y PROBABILIDAD
Martes 14 de Febrero/2012
1. Selección única con única respuesta. Seleccione la respuesta correcta en cada uno de los
siguientes enunciados:
a. Dado el conjunto universal conformado por las letras del abecedario, puede decirse que el conjunto
A = {a, e, i, o, u}es:
I. El complemento del conjunto universal
II. Un conjunto cualquiera dentro del conjunto universal
III. Un conjunto que contiene todos los elementos del conjunto universal
IV. A no es un conjunto pues no tiene elementos que se repitan
b. Seleccione de las siguientes igualdades aquella que es verdadera
I. A – B = B – A
II. (A – B) ∪ (A – C) = A – (B ∪ C)
III. (A – B) ∪ (A – C) = A ∪ (B ∪ C)
IV. (A – B) ∩ (A – C) = A – (B ∪ C)
c. Un promedio alto y una desviación baja indican en un grupo de datos:
I. Que las medidas no son buenas puesto que una varianza muy alta es deseable
II. Que el proceso puede llamarse preciso
III. Que el proceso es altamente disperso
IV. No puede deducirse nada con tan poca información
d. En un proceso aleatorio un evento A tiene probabilidad Pa = 0.75; si el proceso se repite 10 000
veces, cual es el número de veces que el evento A tenderá a ocurrir
I. 0.25
II. 0.000075
III. 7 500
IV. 10 000
e. Cuál de los siguientes no puede considerarse como un proceso estocástico
I. El ruido blanco en un sistema de comunicación
II. La falla de un dispositivo electrónico
III. Los resultados de una operación de suma en una calculadora
IV. El número de encendidos de un bombillo antes de que su filamento se queme
2. En un estudio a un grupo de estudiantes cada estudiante dio la siguiente respuesta a la
pregunta ¿cuál es su color favorito?
Ana – Rosa, Angel – Azul, Angela – Rojo, Arnulfo – Azul, Belisario – Rojo, Beatriz – Azul, Carlos –
Negro, Carolina – Rosa, Damián – Amarillo, Doris – Amarillo, Efraín – Rojo, Ernesto – Amarillo,
Felipe – Amarillo, Graciela – Azúl, Gregorio – Negro, Hilda – Verde, Horacio – Amarillo, Hermes –
Rojo, Imelda – Azul, Julián – Verde
1. ¿Cuál es el conjunto universal de resultados?
2. ¿Cómo se definirían los diferentes conjuntos?

10. 3. ¿Cómo se definirían los conjuntos si se clasifican por letra de inicio del nombre?
4. Realizar la tabla de distribución de frecuencias
5. Calcular las frecuencias relativas para cada uno de los colores
6. ¿Cuál es el espacio muestral?
7. ¿Cuál es la probabilidad de que a un estudiante le guste el color amarillo?
8. ¿Cuál es la probabilidad de que a un estudiante le guste el color verde o rojo?
9. ¿Cuál es la probabilidad de que al elegir a una estudiante al azar a ella le gusto el color rosa?
10. ¿Cuál es la probabilidad de que a un estudiante le guste el color azul y sea hombre?
3. En un estudio sobre un grupo de 10 resistencias de 100 ohms se midieron los siguientes valores:
R1 = 102 ohms, R2 = 100 ohms, R3 = 98 ohms, R4 = 109 ohms, R5 = 97 ohms,
R6 = 104 ohms, R7 = 98 ohms, R8 = 107 ohms, R9 = 96 ohms y R10 = 102 ohms
Se desea obtener un indicador para valores de entre 98 y 102 (100 ± 2%), entre 95 y 105 (100 ± 5%) y
entre 90 y 110 (100 ± 10%), todo en ohms. Para ello obtenga:
a. La definición con la representación por extensión del conjunto universal y de cada subconjunto
necesario
b. La representación en diagramas de Venn de los conjuntos definidos
c. Una tabla completa de frecuencias para cada conjunto
d. Determine sobre el grupo de resistencias las siguientes medidas: promedio, moda, mediana,
varianza, desviación estándar y coeficiente de variación
e. De acuerdo a las medidas dentro del grupo de resistencias determine cuál es la probabilidad de
que una resistencia tomada al azar mida más de 105 ohms
4. Calcule las siguientes probabilidades:
a. La probabilidad de que al lanzar un dado normal se obtengan las caras 2 o 3.
b. La probabilidad de contestar correctamente una pregunta de selección múltiple con única
respuesta cuando la respuesta se deja al azar y son 10 las posibles soluciones.
c. La probabilidad de no obtener “pares” al lanzar dos dados.
d. La probabilidad de que una maquina que genera códigos formados por una letra y un número
genere el código A1.
e. La probabilidad de que al lanzar dos cartas consecutivas de una baraja de naipe español se
obtengan dos ases.
5. En una hoja de cálculo (Excel, OO Calc, etc) genere 10, 100 y 1000 números aleatorios entre 0
y 100 (puede hacerse con la función ALEATORIO()*10, etc). Para los 3 conjuntos de datos
obtenidos calcule en la hoja de cálculo lo siguiente:
a. Promedio y mediana
b. Desviación estándar y varianza
c. La probabilidad de que un número del grupo de datos sea menor a 50
d. Describa el comportamiento de los datos y sus medidas para los grupos de 10, 100 y 1000
números
e. Plantee sus conclusiones

11. SESIÓN 5: CALCULO DE PROBABILIDADES Y PERMUTACIONES
20 de Febrero de 2012
Conteo de puntos de muestra
Espacio muestral: conjunto de todos los posibles resultados de un experimento aleatorio.
Punto o miembro muestral: cada resultado del espacio muestral
Diagrama de árbol de eventos:
Método gráfico para contemplar todos los posibles puntos muestrales de un experimento aleatorio.
Para elaborar el diagrama de árbol se inicia una ramificación desde los resultados posibles en el primer
resultado, estos se ramifican en los resultados posibles para el segundo resultado y así sucesivamente;
se debe tener en cuenta que cada nueva ramificación genera una probabilidad total de 1.
Ejemplo 1:
a. ¿Cuál es la probabilidad de que al lanzar 3 veces una moneda se obtenga en los tres resultados cara?
b. ¿Cuál es la probabilidad de que al lanzar 3 monedas las 3 caigan cara?
Solución:
Diagrama de árbol de eventos del ejemplo 1
a. Se plantea primero el diagrama de árbol; luego se calcula la probabilidad multiplicando la
probabilidad de acuerdo con la ruta (o rutas) que arrojen el resultado buscado; en este caso solamente la
ruta Cara – Cara – Cara es la deseada por tanto la probabilidad para este caso es (1/2)(1/2)(1/2) =
0.125.
b. Al plantear el diagrama de árbol se obtiene el mismo resultado.
Ejemplo 2:
Se tiene un experimento aleatorio en el cuál primero se lanza una moneda, si sale cara la moneda
vuelve a lanzarse, si sale sello se tira un dado.
a. ¿Cuál es la probabilidad de tener que lanzar la moneda una segunda vez?
b. ¿Cuál es la probabilidad de obtener 4 en un dado al finalizar el experimento?
c. ¿Cuál es la probabilidad de no obtener 4 al finalizar el experimento?
Solución:
Se plantea el diagrama de árbol así:

12. Diagrama de árbol de eventos del ejemplo 2
a. La probabilidad será 0.5 puesto que se pide una consecuencia del primer resultado
b. La probabilidad será 0.5*0.16 = 0.08
c. Se busca la probabilidad complemento del evento del literal anterior, es decir que la probabilidad de
no obtener un 4 en el experimento aleatorio será 1 – 0.08 = 0.92
Combinaciones:
As
Regla de multiplicación:
Si una operación se puede llevar a cabo de n formas y para cada una de estas se puede realizar una
operación de m formas entonces las dos operaciones se pueden realizar juntas en n X m formas.
Ejemplo 3:
Al lanzar un par de dados los dos pueden caer de seis formas luego el número total de posibles
resultados será 6 X 6 = 36.
Permutación:
Es un arreglo de una parte o un conjunto de datos; es relevante cuando interés conocer de cuantas
formas pueden ordenarse ciertos elementos. El número de permutaciones de n objetos es n!.
Ejemplo 4:
¿De cuantas formas pueden ordenarse las letras A, B, C y D?
Cómo se trata de 4 letras podrán ordenarse de 4! = 24
ABCD, ABDC, ACBD, ACDB, ADBC, ADCB
BACD, BADC, CABD, CADB, DABC, DACB
DABC, DACB, DBAC, DBCA, DCAB, DCBA
Permutación tomando grupos:
El número de permutaciones de n elementos tomados de r a la vez es:
PGrupos de R=n!/(n - r)!
Ejemplo 5:
¿De cuántas formas pueden ordenarse las letras A, B, C y D si se toman en grupos de a 2?
Se pueden organizar de 4!/(4 – 2)! = 12
AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC

13. Permutación circular:
Una permutación circular sólo se considera diferente si los elementos se arreglan en orden diferente. El
número de permutaciones en un circulo de n elementos es (n – 1)!
Ejemplo 6:
Las combinaciones ABC, CAB y BCA se consideran una sola permutación circular
Permutaciones por grupos:
El número de permutaciones de n cosas de las que n1 son del primer tipo, n2 del segundo tipo, …nk del
k-esimo tipo son: n!/(n1! n2!.... nk!)
Ejemplo 7:
Pueden hacerse 10 combinaciones de letras y números con 2 letras y 3 números:
LLNNN, LNLNN, LNNLN, LNNNL, NLLNN, NLNLN, NLNNL, NNLLN, NNLNL, NNNLL
Combinatoria:
El número de combinaciones de n elementos tomando de a r elementos por combinación es:
Ejemplo 8:
¿De cuántas formas pueden seleccionarse 2 letras del grupo A, B, C y D?
De 4!/ (2! 2!) = 6, AB, AC, AD, BC, BD, CD

14. SESIÓN 6: PROBABILIDAD CONDICIONAL
21 de Febrero de 2012
Probabilidad condicional:
Se llama probabilidad condicional a la probabilidad de que ocurra el evento A dado que se sabe que
ocurrió el evento B y se denota P(A|B). La probabilidad condicional será:
P(A|B) = P(A ∩ B)/P(B)
Ejemplo 1:
¿Cuál es la probabilidad de obtener un número total mayor a 6 si al lanzar le primer dado se obtuvo?
a. 1
b. 6
Solución:
a. Lo primero es calcular la probabilidad de que ocurra un 1 en el dado; esto es P(B)= 1/6
Luego se calcula la probabilidad de que el número total sea mayor a 6 con un 1 en el primer dado, esto
es P(A ∩ B)= 1/36.
Por tanto
P(A|B) = (1/36) / (1/6) = 1/6
b. Procediendo de manera similar se tiene
P(B) = 1/6
P(A ∩ B)= 1
P(A|B) = (1) / (1/6) = 6??
Ejemplo 2:
La probabilidad de que un avión llegue a tiempo es P(L) = 0,82
La probabilidad de que un avión salga a tiempo es P(S) = 0,83
La probabilidad de que un avión llegue y salga a tiempo es P(L ∩ S) = 0,78
a. ¿Cuál es la probabilidad de que el avión llegué a tiempo si salio a tiempo?
b. ¿Cuál es la probabilidad de que el avión salga a tiempo si llegó a tiempo?
Solución:
a. P(L|S) = 0,78/0,83 = 0,9397
b. P(S|L) = 0,78/0,82 = 0,9512
La probabilidad condicional es una medida de actualizar el calculo de la probabilidad dado que se
dispone de información adicional.
Eventos independientes:
Dos eventos son independientes cuando la ocurrencia de alguno no altera la probabilidad de ocurrencia
del otro. Osea
P(A|B) = P(A)
P(A ∩ B) = P(A) P(B)
Ejemplo 3:
¿Cuál es la probabilidad de obtener una cara al lanzar una moneda si anteriormente salido sello?
Solución:
El resultado de lanzar una moneda al aire constituye un evento independiente. Por tanto la
probabilidad será igual a la probabilidad de 0,5, la típica de este experimento.

15. Reglas multiplicativas:
P(A ∩ B) = P(B ∩ A) = P(A|B) = P(B) P(A|B)
Ejemplo 4:
De una baraja de naipe español (40 cartas) se sacan consecutivamente 3 cartas sin remplazo. Obtenga
la probabilidad de que la primera carta sea el as de oros o de espadas, la segunda sea un 10 y la tercera
sea un 2, un 3 o un 4.
Solución:
A = Evento de que la primera carta obtenida sea el as de oros o el as de espadas
P(A) = 2/40
B = Evento de que la segunda carta sea un 10
P(B|A) = 4/39
C = Evento de que la tercera carta sea un 2, un 3 o un 4
P(C| A ∩ B) = 12/38
Finalmente las 3 probabilidades se multiplican para obtener el resultado total:
P(A ∩ B ∩ C) = (1/20) (4/39) (6/19) = 1/195 =0,005128

16. SESIÓN 7: TEOREMA DE LA PROBABILIDAD TOTAL Y REGLA DE BAYES
Lunes 27 de Febrero/2012
Ejercicio de repaso de las sesiones 5 y 6
8 niños Pedro, Paola, Ricardo, Nicolas, Natalia, Esperanza, Carmen, Azucena, deben ubicarse en 8
sillas numeradas y consecutivas.
a. ¿cuál es la probabilidad de que al sentarse los niños en las sillas al azar resulten ordenados
alfabéticamente?
b. si las sillas son ordenadas de forma circular y no se tiene en cuenta su numeración, de cuantas
formas es posible que se sienten los niños?
c. ¿cuantos grupos diferentes formados por 3 niñas y 3 niños se pueden formar?
d. ¿cuál es la probabilidad de que Natalia sea la primera en sentarse dado que la primera sea una niña?
Solución:
a. Sólo puede existir un orden alfabético correcto.
El número total de posiciones es 8! = 40320; la probabilidad es de 1/40320
b. (8 – 1)! = 5040
c. Como solo son 3 niños sólo se puede formar un grupo de niños.
Para saber cuantos grupos de 3 niñas se pueden lograr se utiliza la formula de la combinatoria
obteniendo 5!/(3!(3-1)!) = 10
d. P(A|B) = P(A ∩ B)/P(B) = (1/5)/(5/8) = 8/25, A el evento de que salga Natalia y B el evento de que
la primera en sentarse sea una niña.
Teorema de la probabilidad total (regla de eliminación)
Si los eventos B1, B2, … Bk constituyen una partición del espacio muestral S tal que P(Bi) ≠ 0, para i = 1,
2, … , k, entonces para cualquier evento A de S
Demostración gráfica
Ejemplo:
En un equipo de fútbol todos los disparos de intento de gol son hechos por 3 jugadores: A, B y C. Los
jugadores A y B dispara cada uno el 40% de las veces mientras que C sólo el 20%. Se sabe que cada
uno de los jugadores tiene una efectividad del 10%, 30% y 20% respectivamente;
¿cuál es la probabilidad de hacer 1 gol en un disparo aleatorio?
Rta:
Primero se debe obtener cada una de las probabilidades P(B ∩ A), para ello se plantea el diagrama de
árbol de eventos.

17. Se define el evento A como el evento de marcar un gol y los diferentes eventos B como los eventos de
que cada jugador dispare.
P(BA ∩ A) = 0,4*0,1 = 0,04
P(BB ∩ A) = 0,4*0,3 = 0,12
P(BC ∩ A) = 0,2*0,2 = 0,04
Por tanto la probabilidad de hacer un gol será la sumatoria de estas tres probabilidades, es decir 0,04 +
0,12 + 0,04 = 0,2
Regla de Bayes
La regla de Bayes permite cambiar la pregunta del ejemplo anterior, ahora puede replantearse ¿cuál es
la probabilidad de que un determinado jugador haya disparado si se anotó gol?
La regla de Bayes cita lo siguiente:
Ejemplo:
De acuerdo al ejemplo anterior, ¿cuál es la probabilidad de que si hay gol sea del jugador A? ..del
jugador B? ...del jugador C?
Rta:
P(BA | A) = 0,04/0,2 = 0,2
P(BB | A) = 0,12/0,2 = 0,6
P(BC | A) = 0,04/0,2 = 0,2
Ejemplo:
Se selecciona de una caja con 5 pin pones 2 son rojos y 3 son azules un pin pon y se guarda sin mirarlo
ni saber de que color es; luego en la segunda selección se saca un pin pon de color rojo, ¿cuál es la
probabilidad de que el primer pin pon haya sido rojo?
Rta:
Se establece el diagrama de árbol de eventos, luego se plantean los eventos:
A: Evento de obtener rojo en la primera selección
B: Evento de obtener rojo en la segunda selección
Para poder aplicar el teorema de Bayes y deducir P(A | B) para este caso se debe obtener P(B ∩ A) y
P(B). Del diagrama de árbol se tiene:
P(B ∩ A) = 2/20 = 1/10
B(A) = 2/20 + 6/20 =2/5
Finalmente se tiene P(A | B) = 1/10 / 2/5 = ¼

18. SESIÓN 8 – TALLER 2: COMBINATORIAS Y PERMUTACIONES, PROBABILIDAD
CONDICIONAL, TEOREMA DE PROBABILIDAD TOTAL Y REGLA DE BAYES
Martes 28 de Febrero / 2012
1. De los siguientes enunciados seleccione la respuesta correcta:
a. La probabilidad de falla de un transistor se ha medido respecto a la velocidad de respuesta de un
diodo volante de protección entre el colector y el emisor; ¿cuál de las siguientes es verdadera?
I. Si la probabilidad de falla aumenta al aumentar la velocidad de respuesta del diodo
volante puede decirse que los eventos son independientes.
II. Si la probabilidad de falla disminuye al aumentar la velocidad de respuesta del diodo
volante puede decirse que los eventos son independientes.
III. Si la probabilidad varía puede decirse que los eventos son dependientes.
IV. Si la probabilidad varia puede decirse que los eventos son independientes.
b.¿El método gráfico de diagrama de árbol de eventos para la obtención de espacios muestrales y de las
probabilidades de los puntos muestrales es preferiblemente útil para cuál de los siguiente?
I. Obtener la probabilidad de un experimento que debe repetirse una gran cantidad de
ocasiones.
II. Obtener los puntos muestrales de un experimento que posee 100 posibles resultados y
debe repetirse 2 veces.
III. Obtener los puntos muestrales de un experimento con pocos posibles resultados y pocas
repeticiones.
IV. Ninguno de los anteriores.
c. La diferencia fundamental entre una permutación y una combinación es:
I. En una permutación ninguno de los elementos puede repetirse.
II. En una combinación el orden de los elementos no implica una combinación diferente.
III. En una permutación los elementos se arreglan de manera circular e importa el orden
circular.
IV. Una permutación y una combinación no poseen diferencia.
d. Por medio de la probabilidad condicional se pretende:
I. Calcular la probabilidad de que 2 eventos ocurran simultaneamente.
II. Calcular la probabilidad mediante un método gráfico.
III. Recalcular la probabilidad en base a la no ocurrencia de eventos independientes.
IV. Recalcular la probabilidad en base a la ocurrencia de eventos.
e. Se tienen 2 eventos independientes A y B con probabilidades P(A) y P(B), ¿la probabilidad de que
los 2 eventos sucedan simultaneamente será?
I. P(A|B)
II. P(A) P(B)
III. La regla de Bayes P(A ∩ B)/ (P(A) + P(B))
IV. Cómo son 2 eventos independientes simplemente se suman

19. 2. Determine para cada uno de los siguientes experimentos aleatorios el tamaño del espacio
muestral, es decir el número de combinaciones/permutaciones/etc correspondientes para cada
situación:
a. Lanzar un dado y luego decir una de las 27 letras del alfabeto español
b. Crear un nombre de 5 letras con el alfabeto español, con 3 consonantes y 2 vocales.
c. La forma de diagnosticar a un paciente si se clasifica por tipo de sangre (AB+, AB-, A+, A-, B+, B-,
O+, O-) y presión arterial (alta, media y baja).
d. El número de combinaciones posibles para 2 personas que juegan piedra, papel o tijera.
e. Los valores de las diferentes resistencias equivalentes cuando se usan 4 resistencias en serie de un
grupo conformado por resistencias de 10ohms, 100ohms, 1Kohms, 10Kohms, 100Kohms y 1Mohms;
cada valor solo puede usarse una vez.
3. Para el control de 3 procesos pueden implementarse 3 controladores de tipo microcontrolador,
PLC o PC; solamente puede implementarse un tipo de controlador por proceso. Si el
desarrollador deja al azar la selección de controladores (igualmente probables) para cada
proceso,
a. Dibuje el diagrama de árbol de eventos.
b. ¿cuál es la probabilidad de que el primer proceso sea controlado por un controlador con
microcontroladores, el segundo con un PLC y el tercero con un PC?
c. ¿cuál es la probabilidad de que el primer proceso sea controlado por un PC?
d. ¿cuál es la probabilidad de que el segundo proceso sea controlado por un PC si el tercero es
controlado por un PLC?
e. ¿cuál es la probabilidad de que le tercer proceso sea controlado por un PLC si el segundo proceso
está controlado por un PC?
4. Demuestre gráficamente y explique lo siguiente:
a. Si A y B son eventos independientes entonces P(A ∪ B) = P(A) + P(B)
b. Si A y B son eventos dependientes entonces P(B|A) = P(A ∩ B) / P(A)
c. El teorema de probabilidad total
d. La regla de Bayes
5. Dados los elementos A, B, C, D y E del tipo letras y los elementos 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 del
tipo números obtener en Excel (sólo se permite el uso de fórmulas y referencias a celdas)
a. Número total de combinaciones posibles con 1 letra y 1 número
b. Número de permutaciones de los números en arreglo de 10 (Ej. 1980562374)
c. Número de permutaciones circulares de los números en arreglo de 10
d. Número de combinaciones de las letras tomando de a 3 letras por combinación