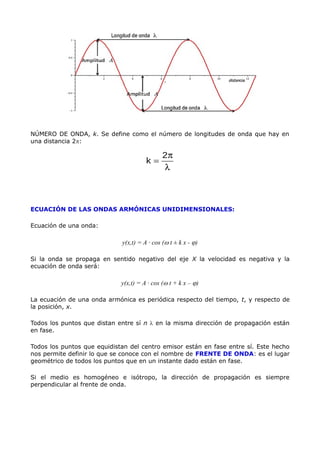
1) Una onda es la propagación de energía a través de un medio sin que haya desplazamiento de materia. 2) Existen dos tipos de ondas: longitudinales, donde la dirección de vibración coincide con la dirección de propagación, y transversales, donde la vibración es perpendicular. 3) Las ondas se caracterizan por su longitud de onda, amplitud y velocidad.