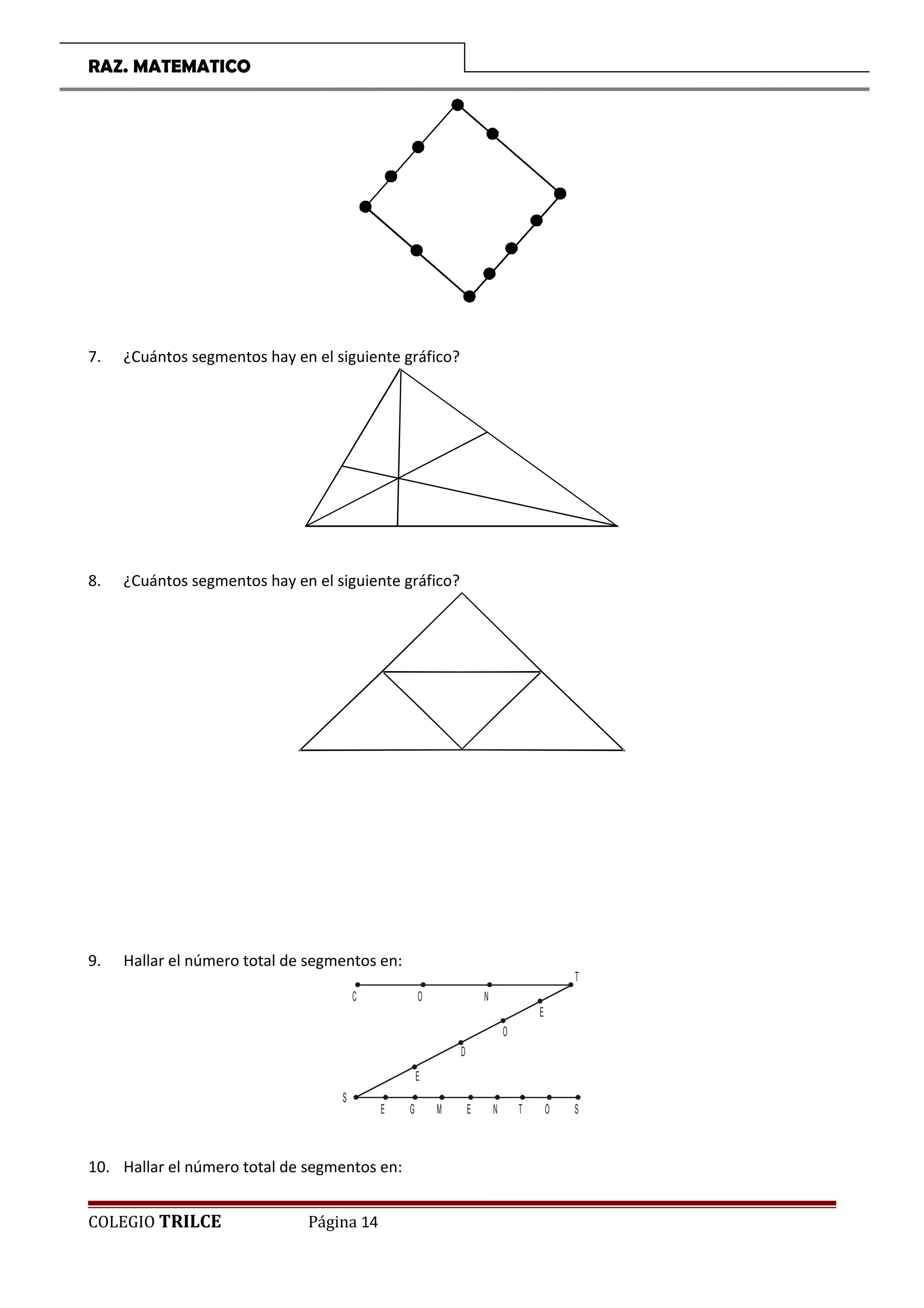
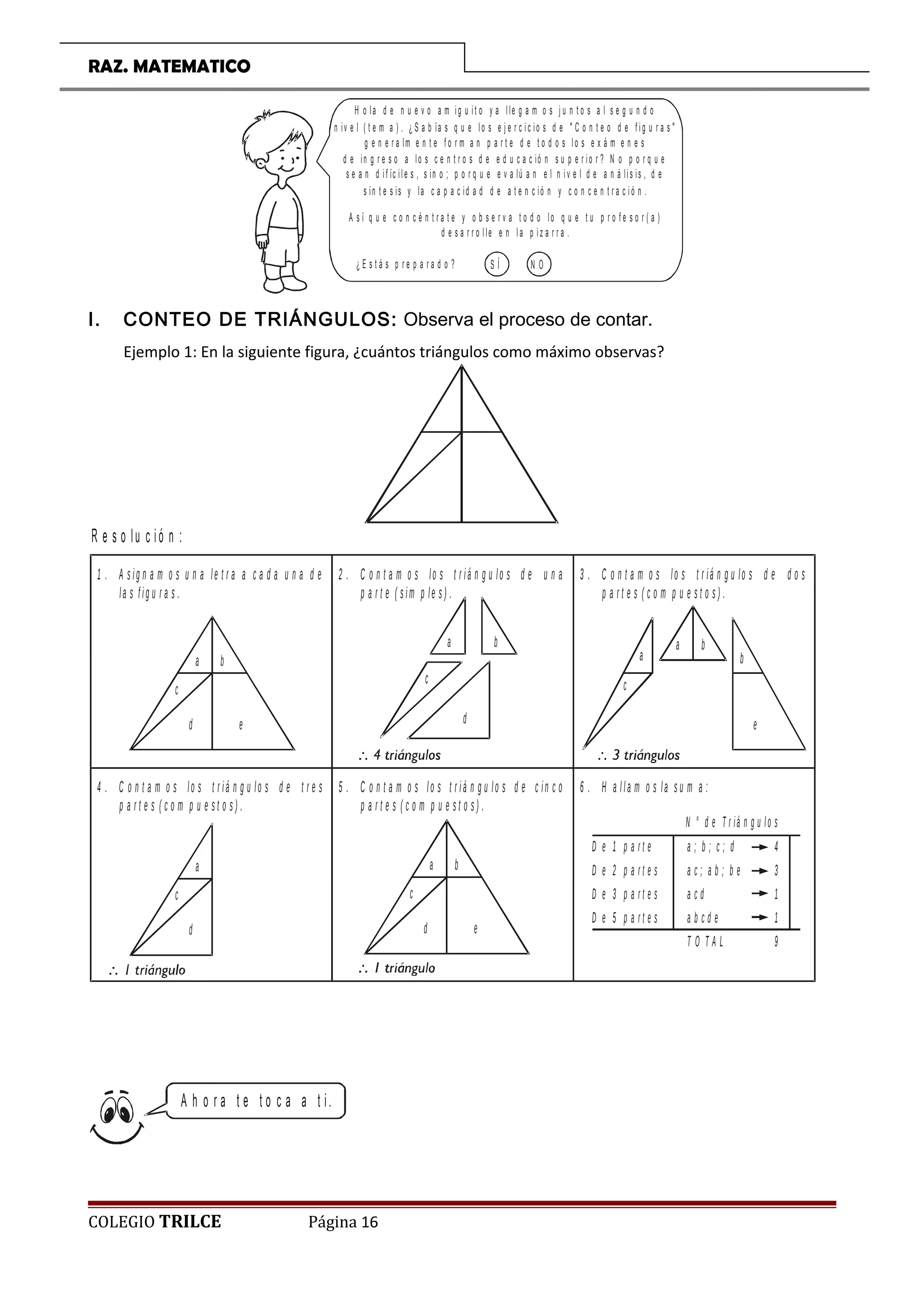
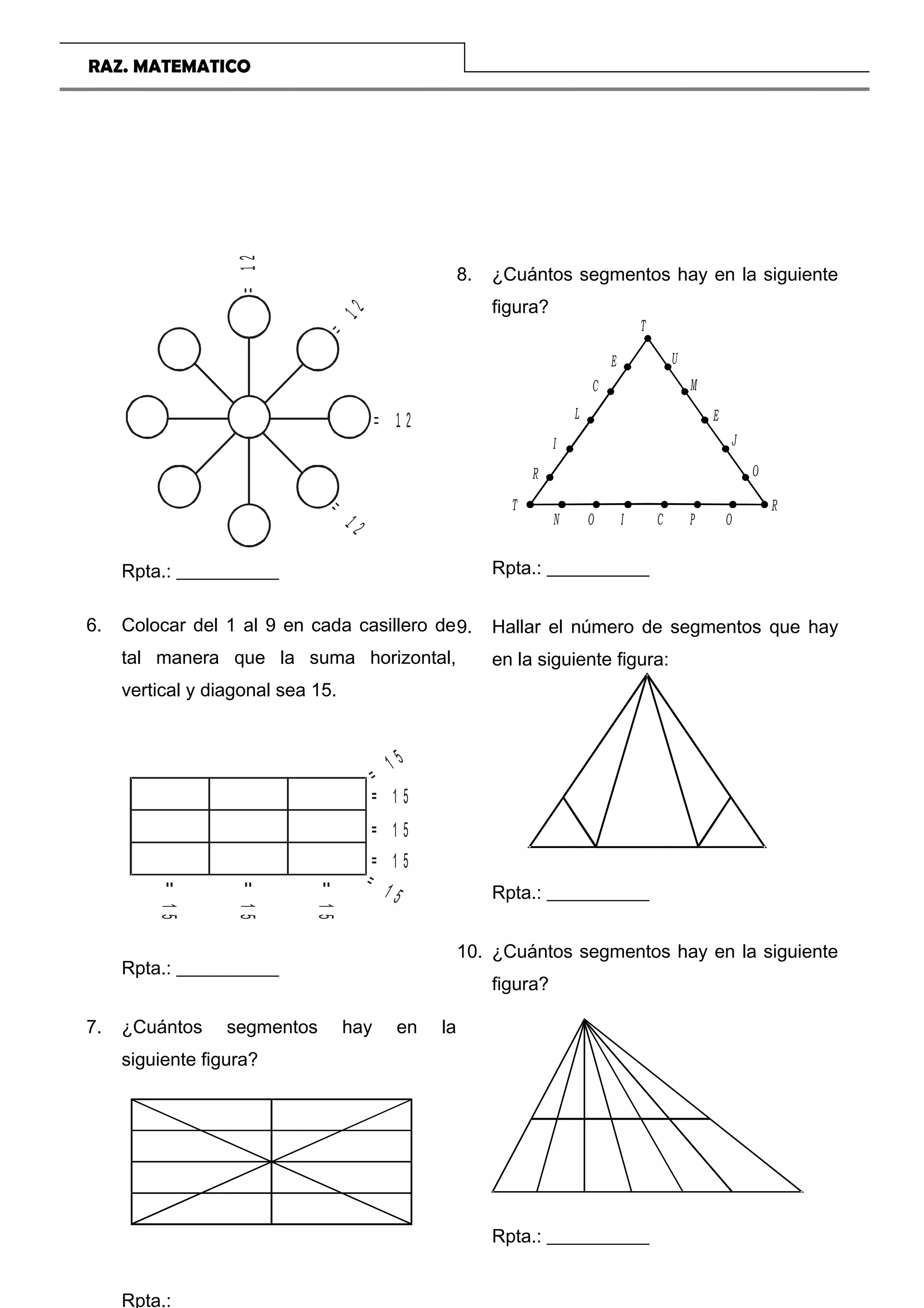
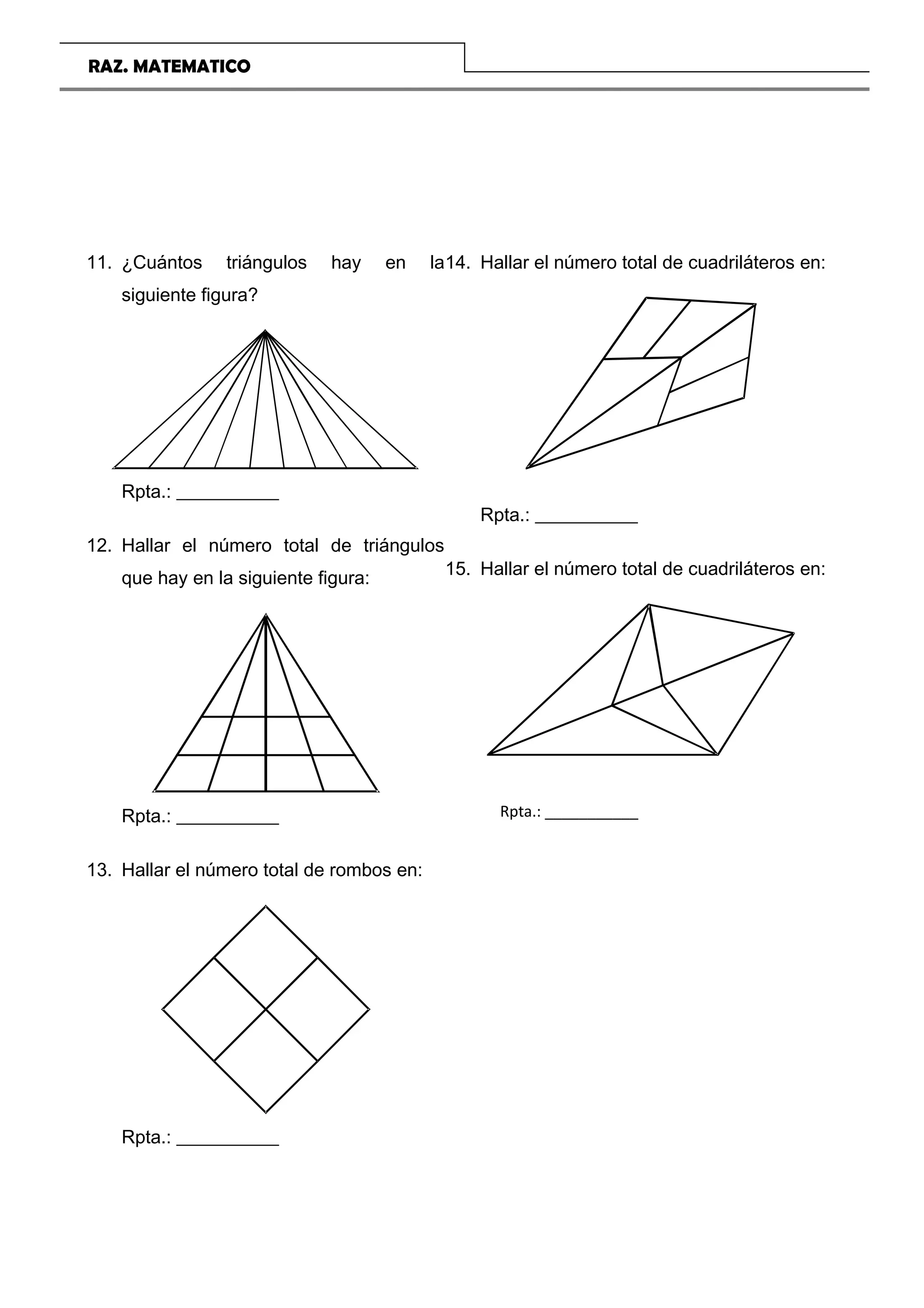
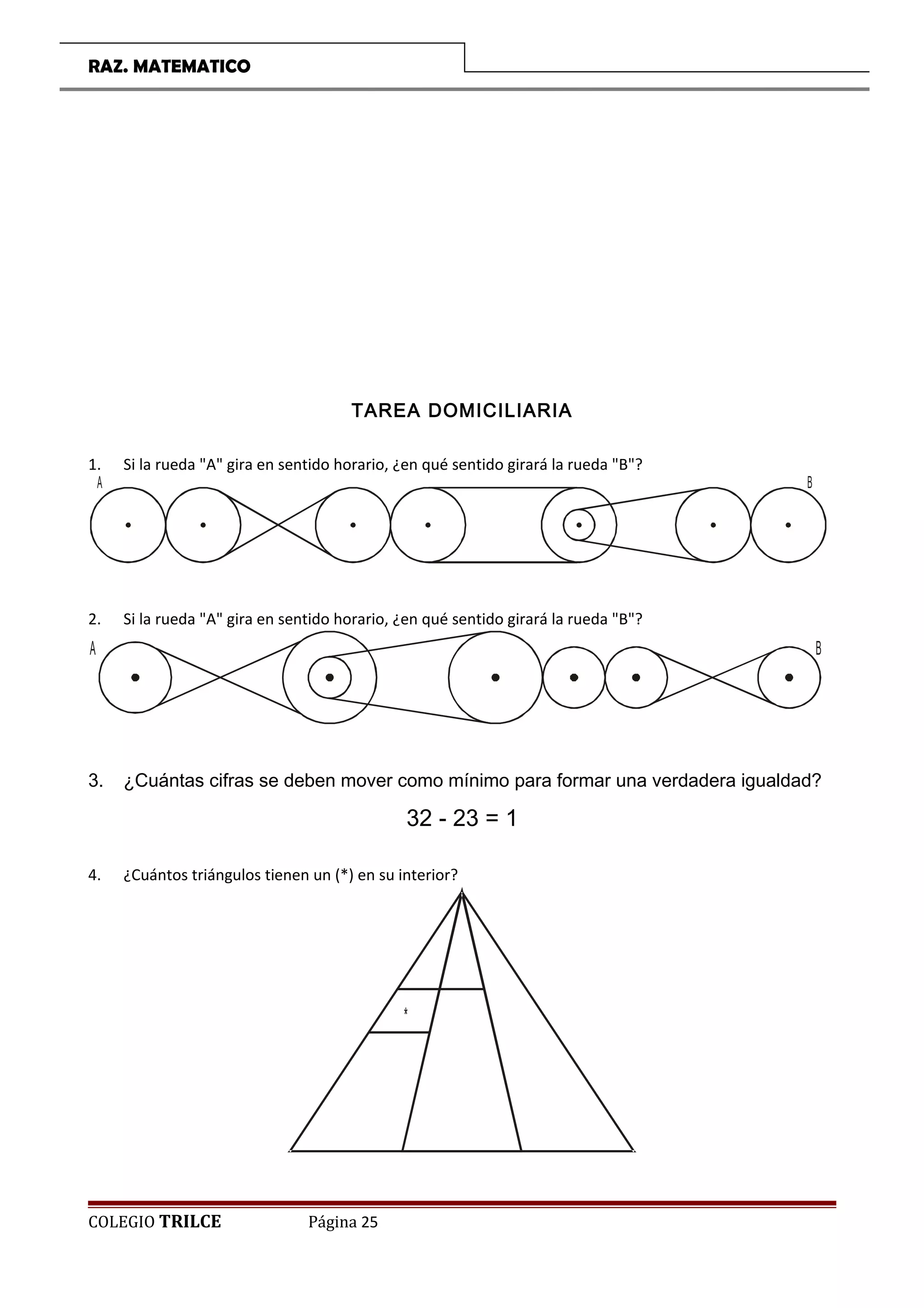
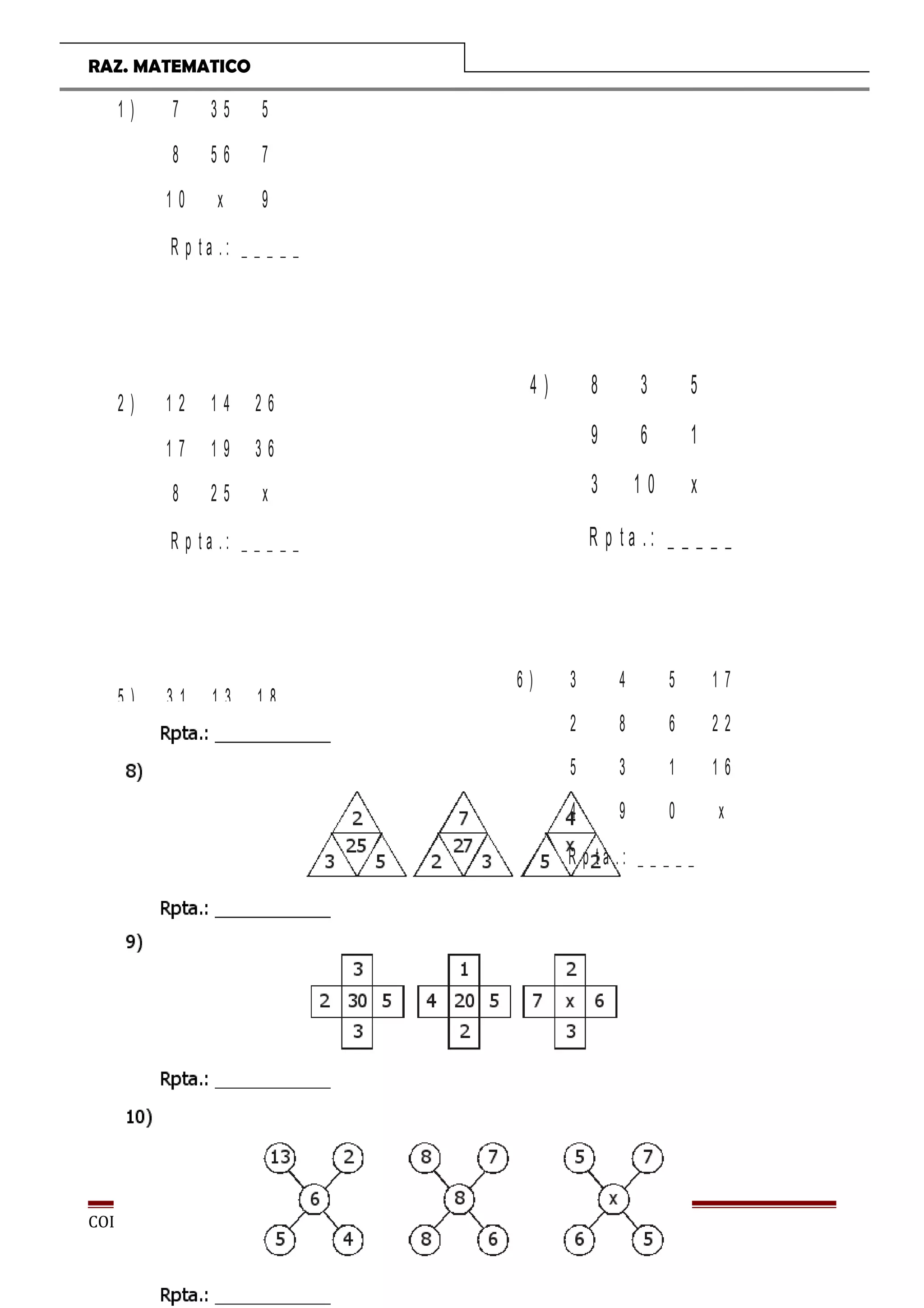
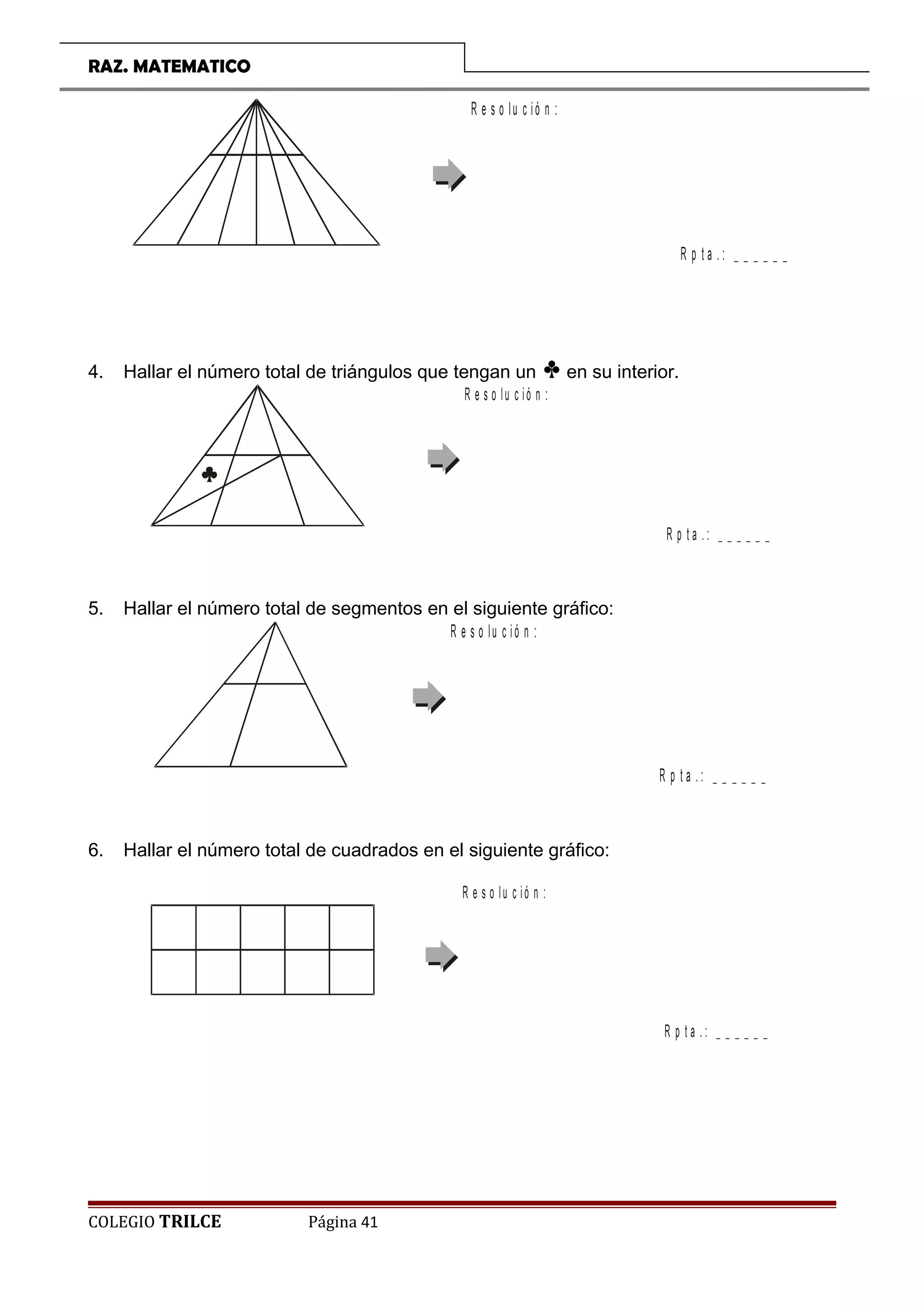
El documento presenta una introducción a un curso de razonamiento matemático para estudiantes de primaria. Incluye temas como matemática recreativa, conteo de segmentos, figuras, sucesiones y retos lógicos. Proporciona ejemplos y ejercicios para que los estudiantes desarrollen su capacidad de resolución de problemas de manera divertida.

1. RAZONAM.
MATEMAT.
I BIM.
TRILCE PRIMARIA

2. RAZ. MATEMATICO
Í n d i c e
Pág.
¯ Matemática recreativa..............................................133
¯ Conteo de segmentos..............................................141
¯ Conteo de figuras.....................................................147
¯ Repaso.....................................................................153
¯ Sucesiones y arreglos literales.................................157
¯ Sucesiones II............................................................163
¯ Distribuciones numéricas.........................................165
¯ EdË`vt fdsdÌ`q#
COLEGIO TRILCE Página 2

3. RAZ. MATEMATICO
¿ E s t á s p r e p a r a d o ? S Í N O
¡ H o la , c ó m o e s t á s ! B ie n v e n id o a e s t a h e r m o s a f a m ilia
T R I L C E , s e g u r o q u e e s t á s m u y c o n t e n t o , j u n t o s
d e s a r r o lla r e m o s e l c u r s o d e “ R a z o n a m ie n t o
M a t e m á t ic o d e u n a f o r m a d iv e r t id a y d id á c t ic a .
E l p r im e r t e m a e s M a t e m á t ic a R e c r e a t iv a , n o
n e c e s it a s s a b e r f ó r m u la s c o m p lic a d a s , n i t e o r e m a s
c o m p le j o s , s ó lo u n p o c o d e in g e n io y h a b ilid a d .
PROBLEMAS SOBRE GIROS
S E N T I D O D E L O S G I R O S
E N E L M O V I M I E N T O
D E R U E D A S O E N G R A N A J E S
S e n t id o H o r a r io
( M o v . d e la s a g u j a s d e l r e lo j )
S e n t id o A n t ih o r a r io
( M o v . e n c o n t r a a l g ir o d e
la s a g u j a s d e l r e lo j )
* Casos:
A B - S i A g ir a e n s e n t id o h o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
- S i A g ir a e n s e n t id o a n t ih o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
→
→
C o n c lu s ió n : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
COLEGIO TRILCE Página 3

4. RAZ. MATEMATICO
A
B
- S i A g ir a e n s e n t id o h o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
- S i A g ir a e n s e n t id o a n t ih o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
→
→
C o n c lu s ió n : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
A - S i A g i r a e n s e n t id o h o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
- S i A g i r a e n s e n t id o a n t ih o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
→
→
C o n c lu s ió n : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
B
B - S i A g ir a e n s e n t id o h o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
- S i A g ir a e n s e n t id o a n t ih o r a r io B
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
→
→
C o n c lu s ió n : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
A
µ Si A gira en sentido horario, ¿podrías decir en qué sentido gira B?
A
B
µ Si A gira en sentido antihorario, ¿en qué sentido gira B?
A
B
COLEGIO TRILCE Página 4

5. RAZ. MATEMATICO
PROBLEMAS DE INGENIO
1. Colocar los números del 1 al 9, uno en cada círculo de tal manera que la suma de cada fila sea 15.
R e c u e r d a q u e lo s
n ú m e r o s n o s e
d e b e n r e p e t ir.
2. Ir desde el 8 hasta el 4 sumando exactamente 29, sin pasar dos veces por el mismo círculo.
8 1 0
1 7 9
9 0 4
R e c u e r d a q u e lo s c a m in o s
s o n h o r iz o n t a le s o v e r t ic a le s
y n o e n d ia g o n a l; e n e s t e
g r á f ic o h a y u n c a m in o
in d ic a d o . ¿ P u e d e s e n c o n t r a r
u n c a m in o m á s c o r t o ?
3. Mover dos fichas de tal manera que cada grupo de fichas sumen 15.
4
7 8
5
1 9
2
6 3
COLEGIO TRILCE Página 5

6. RAZ. MATEMATICO
4. DE UN SOLO TRAZO. Unir los puntos con cuatro líneas rectas, trazadas sin levantar el lápiz del papel,
ni pasar dos veces por una misma línea.
5. Colocar en los círculos de este triángulo los números del 1 al 9 de tal manera que la suma de cada lado
sea 17.
6. Si A gira en sentido antihorario, ¿en qué sentido girará la rueda B?
A B
7. UN SOLO MOVIMIENTO: Moviendo una sola copa, lograr que las llenas y las vacías queden alternadas.
8. Te ofrecen una moneda como la mostrada:
2 5 a . C . ( 2 5 a ñ o s a n t e s d e C r is t o ) .
¿ L a c o m p r a r ía s s i f u e r a s c o le c c io n is t a ?
¿ P o r q u é ?
2 5 a . C .
COLEGIO TRILCE Página 6

7. RAZ. MATEMATICO
9. Cambiando de lugar tres monedas, transformar el triángulo de la figura (I) en el triángulo de la figura
(II).
( I ) ( I I )
10. Si A gira en sentido horario, ¿en qué sentido gira la rueda B?
A
B
RETOS (ACERTIJOS LÓGICOS)
1. Una señora vestida de negro va por flores al cementerio; ¿cómo se llama el difunto?
Rpta.: _________________________
2. A una persona se le cayó su sombrero en una piscina, ¿cómo lo saca?
Rpta.: _________________________
3. ¿Cuántos huevos duros se podrá comer una persona con el estómago vacío?
Rpta.: _________________________
4. ¿A quién hay que matar para que esté contento?
Rpta.: _________________________
COLEGIO TRILCE Página 7

8. RAZ. MATEMATICO
5. ¿Cuál es el hombre que come con los dientes ajenos?
Rpta.: _________________________
TAREA DOMICILIARIA
1. Colocar en los círculos de este triángulo los números del 1 al 9 de tal manera que la
suma de cada lado sea 20.
2. ¿Cuál de las siguientes figuras se puede dibujar sin levantar el lapicero y sin regresar
por el mismo sitio?
I I I I I I
3. Si la rueda A gira en sentido horario, ¿en qué sentido gira la rueda B?
B
A
COLEGIO TRILCE Página 8

9. RAZ. MATEMATICO
4. Si la rueda A gira en sentido horario, ¿en qué sentido gira la rueda B?
A
B
5. Disponer números del 1 al 8 en cada recuadro de tal forma que dos recuadros
vecinos no tengan en su interior dos números consecutivos.
6. ¿Cuántos palitos hay que mover para que la división sea correcta?
COLEGIO TRILCE Página 9

10. RAZ. MATEMATICO
S e g m e n t o e s u n a p o r c ió n d e r e c t a y e s lim it a d a ,
e l s e g m e n t o A B s e d e n o t a a s í: A B
A B
µ Ejemplo 1:
¿Cuántos segmentos, observas en la siguiente figura?
COLEGIO TRILCE Página 10

11. RAZ. MATEMATICO
1 . A s ig n a m o s u n a le t r a m i n ú s c u la a
c a d a p a r t e .
2 . C o n t a m o s lo s s e g m e n t o s d e u n a
p a r t e ( s im p le s ) .
3 . C o n t a m o s s e g m e n t o s d e d o s p a r t e s
( c o m p u e s t o s ) .
4 . C o n t a m o s s e g m e n t o s d e t r e s p a r t e s
( c o m p u e s t o s ) .
5 . C o n t a m o s s e g m e n t o s d e c u a t r o
p a r t e s ( c o m p u e s t o s ) .
R e s o lu c ió n :
P
6 . H a ll a m o s la s u m a .
D e 1 p a r t e
D e 2 p a r t e s
D e 3 p a r t e s
D e 4 p a r t e s
a ; b ; c ; d
a b ; b c ; c d
a b c ; b c d
a b c d
T O T A L
4
3
2
1
1 0
N ° d e S e g m e n t o s
R O F E
a b c d
P R
a
R O
b
O F
c
F E
d
P R O
a b
R O F
b c
O F E
c d
P R O
a b
F
c
R O F
b c
E
d P R O F E
a b c d
Rpta.: El número total de segmentos es 10.
P e r o h a y u n m é t o d o c o r t o u t iliz a n d o u n a f ó r m u la
e s p e c ia l: e s la d e la s u m a d e lo s n p r im e r o s
n ú m e r o s n a t u r a le s
Así:
P R O F E
1 2 3 4
n : C a n t id a d d e s e g m e n t o s p e q u e ñ o s ( s im p le s )
N ° d e S e g m e n t o s =
4 ( 4 + 1 )
2
=
4 ( 5 )
2
=
2 0
2
= 1 0 s e g m e n t o s
µ Ejemplo 2: ¿Cuántos segmentos hay como máximo?
COLEGIO TRILCE Página 11

12. RAZ. MATEMATICO
A B C D E F G
N ° d e S e g m e n t o s = _ _ _ _ _ _ _ =
µ Ejemplo 3:
B
A
C
D
E
F
Rpta.: _______
T e n c u id a d o , p o r q u e la f ó r m u la s e
a p lic a e n u n a lín e a r e c t a s in q u ie b r e .
EJERCICIOS
1. Hallar el número total de segmentos.
A
B
C
D
E
F
G
H
I
J
K
LMN
2. Hallar el número total de segmentos.
COLEGIO TRILCE Página 12

13. RAZ. MATEMATICO
L
T
R
I
C E P R I
M
A
R
I
ALOMAXIMO
3. Hallar el número total de segmentos.
4. Hallar el número total de segmentos.
5. Hallar el número total de segmentos de:
P
E
D
R
O
G
O
M
E
Z
6. Hallar el número total de segmentos de:
COLEGIO TRILCE Página 13

14. RAZ. MATEMATICO
7. ¿Cuántos segmentos hay en el siguiente gráfico?
8. ¿Cuántos segmentos hay en el siguiente gráfico?
9. Hallar el número total de segmentos en:
C O N
T
E
O
D
E
S
E G M E N T O S
10. Hallar el número total de segmentos en:
COLEGIO TRILCE Página 14

15. RAZ. MATEMATICO
O
R
A
Z
N A M I E N
T
O
M
A
TEMATICO
TAREA DOMICILIARIA
Hallar el número total de segmentos de:
T R I L C E P R I M A R I A
1 .
A B C D E F G H I J K L M N Ñ O
2 .
3 .
R
M
T
U
C
U
R
S
O
P
R
E
F
E
R
I
D
O
D4 . E F G H I J
K
L
M
N
ÑOPQRSTU
A
B
C
COLEGIO TRILCE Página 15
5 .

16. RAZ. MATEMATICO
H o la d e n u e v o a m ig u it o y a l le g a m o s j u n t o s a l s e g u n d o
n iv e l ( t e m a ) . ¿ S a b ía s q u e lo s e j e r c i c io s d e C o n t e o d e f i g u r a s
g e n e r a lm e n t e f o r m a n p a r t e d e t o d o s l o s e x á m e n e s
d e in g r e s o a lo s c e n t r o s d e e d u c a c ió n s u p e r io r ? N o p o r q u e
s e a n d i f íc ile s , s in o ; p o r q u e e v a lú a n e l n i v e l d e a n á lis is , d e
s ín t e s is y la c a p a c id a d d e a t e n c ió n y c o n c e n t r a c i ó n .
A s í q u e c o n c é n t r a t e y o b s e r v a t o d o lo q u e t u p r o f e s o r ( a )
d e s a r r o l le e n l a p i z a r r a .
¿ E s t á s p r e p a r a d o ? S Í N O
I. CONTEO DE TRIÁNGULOS: Observa el proceso de contar.
Ejemplo 1: En la siguiente figura, ¿cuántos triángulos como máximo observas?
1 . A s ig n a m o s u n a le t r a a c a d a u n a d e
la s f ig u r a s .
a b
c
d e
2 . C o n t a m o s lo s t r iá n g u lo s d e u n a
p a r t e ( s im p le s ) .
a b
c
d
3 . C o n t a m o s lo s t r iá n g u lo s d e d o s
p a r t e s ( c o m p u e s t o s ) .
a b
e
ba
c
4 . C o n t a m o s lo s t r iá n g u lo s d e t r e s
p a r t e s ( c o m p u e s t o s ) .
a
c
d
5 . C o n t a m o s lo s t r iá n g u lo s d e c in c o
p a r t e s ( c o m p u e s t o s ) .
a b
c
d e
6 . H a lla m o s la s u m a :
D e 1 p a r t e
D e 2 p a r t e s
D e 3 p a r t e s
D e 5 p a r t e s
a ; b ; c ; d
a c ; a b ; b e
a c d
a b c d e
T O T A L
4
3
1
1
9
N ° d e T r iá n g u lo s
R e s o lu c ió n :
A h o r a t e t o c a a t i.
COLEGIO TRILCE Página 16

17. RAZ. MATEMATICO
Ejemplo 2:
¿Cuántos triángulos hay como máximo en la siguiente figura?
1
2
3
4
5
P r e g u n t a a t u p r o f e s o r s i h a y
a lg ú n m é t o d o c o r t o p a r a
la r e s o lu c ió n d e e s t e p r o b le m a .
Anota lo que tu profesor te diga.
EJERCICIOS
COLEGIO TRILCE Página 17

18. RAZ. MATEMATICO
1. ¿Cuántos triángulos hay como máximo en la siguiente figura?
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
2. ¿Cuántos triángulos hay como máximo en la siguiente figura?
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
3. Hallar el número total de triángulos en:
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
4. Hallar el número total de triángulos en:
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
5. ¿Cuántos triángulos tienen un (*) asterisco en su interior?
COLEGIO TRILCE Página 18

19. RAZ. MATEMATICO
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
II. CONTEO DE CUADRILÁTEROS: Observa el proceso de contar.
Ejemplo 1: ¿Cuántos rectángulos como máximo observas?
1 . S e a s ig n a u n a le t r a a c a d a p a r t e .
a
2 . C o n t a m o s lo s r e c t á n g u lo s d e u n a
s o la p a r t e .
3 . C o n t a m o s lo s r e c t á n g u lo s q u e s e
fo r m a n c o n d o s p a r t e s ( c o m p u e s t o s ) .
4 . C o n t a m o s lo s r e c t á n g u lo s q u e s e
f o r m a n c o n t r e s p a r t e s ( c o m -
p u e s t o s ) .
H a y _ _ _ _ r e c t á n g u lo s
5 . C o n t e m o s e l t o t a l d e r e c t á n g u lo s .
1
2
3
a ; b ; c ; d ; e ; f
_ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _
T O T A L
_ _ _
_ _ _
_ _ _
_ _ _
N ° d e R e c t á n g u lo s
R e s o lu c ió n :
b c
d e
f
a
b c
d e
f
b
e
b c
d e
H a y _ _ _ _ r e c t á n g u lo s
a
b c
d e
f
H a y _ _ _ _ r e c t á n g u lo s
N ° d e Pa r t e s
EJERCICIOS
COLEGIO TRILCE Página 19

20. RAZ. MATEMATICO
1. ¿Cuántos cuadriláteros hay?
2. Hallar el número total de cuadrados.
3. Hallar el número total de rectángulos.
4. Hallar el número total de cuadrados.
COLEGIO TRILCE Página 20

21. RAZ. MATEMATICO
5. Hallar el número total de rectángulos y cuadrados en el siguiente gráfico y colocar a
cada afirmación V si es verdadero y F si es falso:
I. El total de rectángulos es 9...........................................................( )
II. El número total de cuadrados es 6...............................................( )
III. Hay tres rectángulos más que cuadrados....................................( )
TAREA DOMICILIARIA
COLEGIO TRILCE Página 21
1. Hallar el número total de cuadrados.
2. Hallar el número total de rectángulos en la
siguiente figura:
3. ¿Cuántos paralelogramos hay?
4. Hallar el número total de triángulos en el
siguiente gráfico:
5. Hallar el número total de cuadrados.

22. RAZ. MATEMATICO
H o y h a r e m o s u n r e p a s o d e lo s t r e s t e m a s
q u e h e m o s v is t o h a s t a a h o r a .
S i n o h a s c o m p r e n d id o a lg u n o s
p r o b le m a s , lo h a r á s e n
e s t e r e p a s o . ¡ A P R O V É C H A L O !
EJERCICIOS
COLEGIO TRILCE Página 22
1. Si la rueda A gira en sentido horario,
¿en qué sentido gira la rueda B?
A
B
Rpta.: ___________
2. ¿Cuántas cifras se deben mover como
mínimo para formar una verdadera
igualdad?
13 - 32 = 4
Rpta.: ___________
3. Si la rueda A gira en sentido horario,
¿en qué sentido gira la rueda B?
A
B
Rpta.: ___________
4. Coloca los números del 1 al 9 en los
círculos de la figura mostrada (sin
repetirlos), de tal manera que la hilera
vertical y horizontal sumen lo mismo y
ésta sea igual a 27. ¿Cuál es la cifra que
debe estar en el círculo central?
Rpta.: ___________
5. Colocar los números del 1 al 9 en los
círculos de la figura mostrada (sin
repetirlos), de tal manera que todas las
hileras formadas por tres círculos sumen
lo mismo y ésta sea igual a 12. ¿Cuál es
la cifra que debe estar en el círculo
central?

23. RAZ. MATEMATICO
COLEGIO TRILCE Página 23
= 1 2
=
1 2
=
12
=12
Rpta.: ___________
6. Colocar del 1 al 9 en cada casillero de
tal manera que la suma horizontal,
vertical y diagonal sea 15.
=15
= 1 5
= 1 5
= 1 5
=15
=15
=
1 5
=
1 5
Rpta.: ___________
7. ¿Cuántos segmentos hay en la
siguiente figura?
Rpta.: ___________
8. ¿Cuántos segmentos hay en la siguiente
figura?
R
I
L
C
T
E
T
U
M
E
J
O
R
OPCION
Rpta.: ___________
9. Hallar el número de segmentos que hay
en la siguiente figura:
Rpta.: ___________
10. ¿Cuántos segmentos hay en la siguiente
figura?
Rpta.: ___________

24. RAZ. MATEMATICO
COLEGIO TRILCE Página 24
11. ¿Cuántos triángulos hay en la
siguiente figura?
Rpta.: ___________
12. Hallar el número total de triángulos
que hay en la siguiente figura:
Rpta.: ___________
13. Hallar el número total de rombos en:
Rpta.: ___________
14. Hallar el número total de cuadriláteros en:
Rpta.: ___________
15. Hallar el número total de cuadriláteros en:
Rpta.: ___________

25. RAZ. MATEMATICO
TAREA DOMICILIARIA
1. Si la rueda A gira en sentido horario, ¿en qué sentido girará la rueda B?
A B
2. Si la rueda A gira en sentido horario, ¿en qué sentido girará la rueda B?
A B
3. ¿Cuántas cifras se deben mover como mínimo para formar una verdadera igualdad?
32 - 23 = 1
4. ¿Cuántos triángulos tienen un (*) en su interior?
*
COLEGIO TRILCE Página 25

26. RAZ. MATEMATICO
5. ¿Cuántos segmentos hay en la siguiente figura?
Q u e r id o a m ig o , e l t e m a q u e d e s a r r o lla r e m o s
h o y e s u n o d e m is f a v o r it o s ; y o s é q u e t a m b ié n
s e r á d e t u a g r a d o , m e r e f ie r o , a l t e m a d e
S u c e s i o n e s y A r r e g l o s L i t e r a l e s .
P e r o ¿ q u é e s u n a s u c e s ió n ? V e a m o s e l c o n c e p t o .
SUCESIÓN:
Es un conjunto ordenado de números de acuerdo a una ley de formación. Dichos números son los términos
de la sucesión.
P o r e j e m p lo , e l s ig u ie n t e c o n j u n t o o r d e n a d o d e n ú m e r o s :
1 ; 3 ; 5 ; 7 ; 9 ; . . . t ie n e u n a le y d e f o r m a c ió n .
En efecto, si aumentamos dos unidades a cada uno de los números, obtendremos el
siguiente.
Por lo tanto: (1; 3; 5; 7; 9; . . . ) es una SUCESIÓN, donde los términos mantienen un
orden y se les nombra del modo siguiente:
1: primer término
3: segundo término
COLEGIO TRILCE Página 26

27. RAZ. MATEMATICO
5: tercer término
7: cuarto término, etc.
A h o r a v e a m o s o t r a s u c e s ió n : 5 ; 7 ; 1 0 ; 1 4 ; . . .
¿ P o d r ía s h a lla r e l t é r m in o q u e s ig u e ?
Para resolver este problema, debemos encontrar la ley de formación, como se muestra a continuación:
5 ; 7 ; 1 0 ; 1 4 ; . . .
+ 2 + 3 + 4 + 5
Por lo tanto el número que sigue deberá ser: 14 + 5; esto es 19.
ARREGLOS LITERALES:
Es un conjunto ordenado de letras de acuerdo a un determinado criterio. Para encontrar el
criterio de ordenamiento de las letras en un problema dado, es necesario conocer bien el
abecedario, tener en cuenta la posición de cada letra y no se debe considerar las letras
compuestas CH y LL.
P o r e j e m p lo : ¿ Q u é le t r a s ig u e ?
A ; C ; F ; J ; . . .
Este arreglo tiene cierto criterio de ordenamiento. En efecto, observemos lo siguiente:
A ; C ; F ; J
B D E G H I
Entre A y C hay una letra intermedia;
entre C y F hay dos letras intermedias;
entre F y J hay tres letras intermedias.
Por lo tanto entre J y la letra que sigue deben haber cuatro letras intermedias.
A ; C ; F ; J ; . . .
B D E G H I K L M N
COLEGIO TRILCE Página 27

28. RAZ. MATEMATICO
Entonces la letra que sigue es: ______
Nota: Se puede resolver el problema anterior de otra manera, lo único que necesitamos saber es, la
posición que ocupa cada letra del arreglo dado, en el abecedario.
A
1
B C D E F G H I J K L M N
2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4
Ñ
1 5
O P Q R S T U V W X Y Z
1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7
R e c u e r d a q u e n o s e c o n s id e r a n la s le t r a s
c o m p u e s t a s C H y L L e n a r r e g lo s lit e r a le s .
Ahora observa cómo se resuelve el problema anterior, pasando del arreglo literal a una
SUCESIÓN:
A ; C ; F ; J ; . . .
1 ; 3 ; 6 ; 1 0 ; . . .
P o s ic ió n e n
e l a b e c e d a r io
+ 2 + 3 + 4 + 5
Ñ
1 5
Como verás, el número que sigue en la sucesión es 15, ahora sólo tenemos que buscar
la letra que ocupa la posición número 15 en el abecedario y ésta es la letra Ñ.
¡ A h o r a , h a z lo t ú !
¿ Q u é le t r a s ig u e e n e l s ig u ie n t e a r r e g lo lit e r a l?
C ; F ; J ; M ; P ; . . .
COLEGIO TRILCE Página 28

29. RAZ. MATEMATICO
C ; F ; J ; M ; P ; . . .
R p t a . : _ _ _ _ _ _ _
EJERCICIOS PARA LA CLASE
I. Encontrar el número que sigue en cada una de las siguientes sucesiones:
COLEGIO TRILCE Página 29
1) 7; 10; 15; 22; . . .
2) 3; 9; 5; 15; 11; . . .
3) 2; 2; 4; 12; . . .
4) 64; 32; 16; . . .
5) 2; 4; 8; 14; . . .
6) 2; 3; 4; 7; 8; 11; . . .
7) 5; 3; 6; 4; 8; 6; 16; . . .
8) 1; 1; 2; 6; . . .
9) 2; 3; 4; 5; 8; 7; 16; . . .
10) 18; 16; 12; 6; . . .
11) 10; 12; 6; 8; 4; . . .
12) 3; 4; 8; 5; 9; 45; . . .

30. RAZ. MATEMATICO
II. Encontrar la letra que sigue en cada uno de los siguientes arreglos literales:
TAREA DOMICILIARIA
I. Hallar el número que sigue en cada una de las siguientes sucesiones.
1) 2; 5; 10; 13; 18; . . .
COLEGIO TRILCE Página 30
1) A; D; G; J; . . .
2) B; D; G; I; L; . . .
3) A; D; I; O; . . .
4) B; C; F; G; N; . . .
5) A; B; D; D; G; F; J; . . .
6) B; C; E; H; L; . . .

31. RAZ. MATEMATICO
2) 2; 3; 6; 13; 18; 23; . . .
3) 26; 18; 11; 5; . . .
4) 4; 8; 5; 10; 7; 14; . . .
5) 5; 6; 12; 9; 10; 20; . . .
II. Hallar la letra que sigue en cada uno de los siguientes arreglos literales.
1) A; C; B; D; C; E; . . .
2) W; L; F; . . .
3) C; D; G; L; . . .
4) A; A; B; D; G; K; . . .
5) A; B; D; H; . . .
COLEGIO TRILCE Página 31

32. RAZ. MATEMATICO
E n e s t e c a p ít u lo v e r e m o s u n a g r a n v a r ie d a d
d e s u c e s io n e s y t e n e m o s q u e e n c o n t r a r la le y
d e f o r m a c ió n d e c a d a u n a d e e lla s , p a r a lu e g o
h a lla r la q u e n o s p id e n .
EJERCICIOS PARA LA CLASE
I. Encontrar el número que sigue en cada una de las siguientes sucesiones:
1) 3; 4; 8; 11; 12; 24; 27; . . .
2) 2; 3; 6; 6; 18; 9; 54; . . .
3) 1; 1; 1; 2; 12; . . .
4) 1; 3; 8; 17; 31; . . .
5) 3; 3; 5; 9; 15; . . .
COLEGIO TRILCE Página 32

33. RAZ. MATEMATICO
II. Encontrar el valor de x + y en cada una de las siguientes sucesiones:
1) 3; 1; 4; 2; 8; 6; x; y; . . .
2) 2; 5; 4; 6; 8; 7; x; y; . . .
3) 1; 3; 4; 7; 11; x; y; . . .
4) 3; 4; 6; 10; 18; 16; x; y; . . .
5) 1; 1; 2; 3; 4; 5; 8; 7; x; y; . . .
TAREA DOMICILIARIA
1. ¿Qué número sigue?
4; 5; 7; 10; 14; 19; . . .
2. ¿Qué número sigue en la siguiente sucesión?
2; 6; 3; 9; 6; 18; . . .
3. ¿Qué número sigue?
1; 17; 32; 44; 51; . . .
4. Hallar x + y en:
4; 9; 12; 17; 20; x; y; . . .
5. Hallar y - x en:
1; 3; 2; 6; 4; 9; 8; x; y; . . .
COLEGIO TRILCE Página 33

34. RAZ. MATEMATICO
O b s e r v a c ó m o s e h a n d is t r ib u id o lo s n ú m e r o s e n
c a d a u n a d e la s s ig u ie n t e s f ig u r a s :
1 9
4 2
2 1 7
3 5
5 x
6 3
¿ P o d r ía s h a lla r e l v a lo r d e x ?
Claro que sí, sólo tenemos que buscar la relación que existe entre los demás
números dados.
Veamos:
De la primera figura tenemos que: 4 × 2 + 1 = 9 y
de la segunda figura tenemos que: 3 × 5 + 2 = 17
Como verás, se ha encontrado una misma relación para las dos primeras figuras y
esa relación se debe dar también en la tercera figura.
Por lo tanto; de la tercera figura tenemos que: x = 6 × 3 + 5.
Es decir el valor de x es 23
COLEGIO TRILCE Página 34

35. RAZ. MATEMATICO
A h o r a v e a m o s u n a d is t r ib u c ió n lit e r a l.
A B
F
C
C D
L
E
E F
?
G
¿ Q u é le t r a f a lt a ?
Para resolver este problema, sólo basta con reemplazar cada una de las letras con
los números que indican la posición de éstas en el abecedario.
Así tenemos:
1 2
6
3
3 4
1 2
5
5 6
?
7
De la primera figura se tiene que: 1 + 2 + 3 = 6 y de la segunda figura se tiene que:
3 + 4 + 5 = 12
Por lo tanto; en la tercera figura el número que falta es: 5 + 6 + 7; esto es 18.
Entonces tenemos que buscar la letra número 18 en el abecedario y ésta es la letra
Q.
EJERCICIOS PARA LA CLASE
I. Hallar el valor de x en cada una de las siguientes distribuciones numéricas.
COLEGIO TRILCE Página 35
3 ) 4
2
5
3
9
7
2 6
3 6
x
R p t a . : _ _ _ _ _

36. RAZ. MATEMATICO
1 ) 7
8
1 0
3 5
5 6
x
5
7
9
R p t a . : _ _ _ _ _
2 ) 1 2
1 7
8
1 4
1 9
2 5
2 6
3 6
x
R p t a . : _ _ _ _ _
5 ) 3 1
1 7
9 1
1 3
1 0
x
1 8
2 0
3 4
R p t a . : _ _ _ _ _
7)
58
5
75
73
1
45
21 8
x
56
COLEGIO TRILCE Página 36
4 ) 8
9
3
3
6
1 0
5
1
x
R p t a . : _ _ _ _ _
6 ) 3
2
5
4
4
8
3
9
5
6
1
0
1 7
2 2
1 6
x
R p t a . : _ _ _ _ _

37. RAZ. MATEMATICO
II. Hallar la letra que falta en cada una de las siguientes distribuciones literales:
1)
C
A
F
B E
C
N
J F
G
?
J
Rpta.: _______
COLEGIO TRILCE Página 37

38. RAZ. MATEMATICO
2)
C
D
A F
E
F
C H
D
?
B J
Rpta.: _______
3)
I
B D
O
E C
?
A G
Rpta.: _______
4)
B
E
G
H
Ñ
?
D
C
C
Rpta.: _______
5)
Rpta.: _______
TAREA DOMICILIARIA
I. Hallar el valor de x en cada caso:
1 ) 4
1 2
1 1
3 6
7 2
( x )
9
6
1 3
2 ) 8
1 6
2 3
( 2 1 )
( 3 4 )
( x )
1 3
1 8
3 1
3 ) 1 3
4 5
1 0 6
( 1 0 )
( 1 8 )
( x )
2 4
1 8
3 7
R p t a . : _ _ _ _ _ _ _ R p t a . : _ _ _ _ _ _ _ R p t a . : _ _ _ _ _ _ _
COLEGIO TRILCE Página 38
B
C
E
C
D
A
G
M
?

39. RAZ. MATEMATICO
II. Hallar la letra que falta en cada caso:
4)
C F
J
H
D J
Ñ
X
B L
?
K
5)
F
J B
C
G H
?
I E
COLEGIO TRILCE Página 39

40. RAZ. MATEMATICO
¿ C ó m o e s t á s a m ig u it o ? É s t a e s n u e s t r a ú lt im a c la s e
d e l p r im e r b im e s t r e , s ie n t o u n a in m e n s a a le g r ía a l
s a b e r q u e h a s a p r e n d id o m u c h o .
H o y r e p a s a r e m o s lo s t e m a s d e : M a t e m á t ic a R e c r e a t iv a ,
C o n t e o d e F ig u r a s I y I I , S u c e s io n e s I y I I y D is t r ib u c io n e s .
T ie n e s q u e a p r o v e c h a r e s t e r e p a s o a l m á x im o , p u e s
y a s e v ie n e la e v a lu a c ió n b im e s t r a l. ¿ N e r v io s o ( a ) ? n o t e
p r e o c u p e s q u e y o t e a c o m p a ñ o .
PROBLEMAS
1. La siguiente columna de cinco filas contiene 15 cifras impares.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
1
3
5
7
9
1
3
5
7
9
1
3
5
7
9
El problema consiste en tachar nueve cifras. Eligiéndolas de manera, que al sumar
las columnas de las seis cifras restantes se obtenga el número 111.
2. Hallar el número total de cuadrados en:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
3. ¿Cuántos triángulos hay en el siguiente gráfico?
COLEGIO TRILCE Página 40

41. RAZ. MATEMATICO
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
4. Hallar el número total de triángulos que tengan un p en su interior.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
5. Hallar el número total de segmentos en el siguiente gráfico:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
6. Hallar el número total de cuadrados en el siguiente gráfico:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
COLEGIO TRILCE Página 41

42. RAZ. MATEMATICO
7. Hallar el número total de rectángulos.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
8. Hallar el número total de cuadriláteros.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
9. Hallar el número total de segmentos.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n :
10. ¿Qué números siguen en las siguientes sucesiones?
3; 4; 7; 12; . . . . ; . . . . .
2; 3; 6; 2; -2; 3 . . . . ; . . . . .
Rpta.: _______
11. ¿Qué letras siguen en los siguientes arreglos literales?
A; B; D; H; . . . . .
COLEGIO TRILCE Página 42

43. RAZ. MATEMATICO
E; F; H; K; . . . . ; . . . . .
Rpta.: _______
TAREA DOMICILIARIA
1. Si la rueda A gira en sentido antihorario, ¿en qué sentido gira B?
COLEGIO TRILCE Página 43
12. ¿Qué número falta?
15 (40) 25
→
17 (97) 80
→
23 (x) 60
→
Rpta.: ____________
13. ¿Qué número falta?
18 (6) 12
→
14. Hallar el valor de x.
12 3 11
→
3 15 6
→
4 1 x
→
Rpta.: ____________
15. Hallar el valor de x.
3 6 8
→

44. RAZ. MATEMATICO
A
B
2. Hallar el número total de triángulos.
3. ¿Qué número sigue en la siguiente sucesión?
12; 24; 14; 22; 16; 20; . . . . .
4. ¿Qué letra continúa?
G; J; M; 0; . . . . .
5. Hallar el valor de x.
4
1 7
5
2 6
8
1 9
1
3 7
1
x
4
5 3
6. ¿Cuántos segmentos hay en el siguiente gráfico?
COLEGIO TRILCE Página 44

45. RAZ. MATEMATICO
A N D R E A
7. Si la rueda A gira en sentido horario, ¿cuántas de estas ruedas girarán en
sentido antihorario?
A
8. Hallar el total de triángulos en la siguiente figura:
9. ¿Qué número sigue?
1; 2; 4; 7; 11; . . .
COLEGIO TRILCE Página 45

46. RAZ. MATEMATICO
10. ¿Qué número falta?
4 7
6
3
2 0 1 2 8
9
5
3 4 1 1 6
1 4
2 5
x
COLEGIO TRILCE Página 46