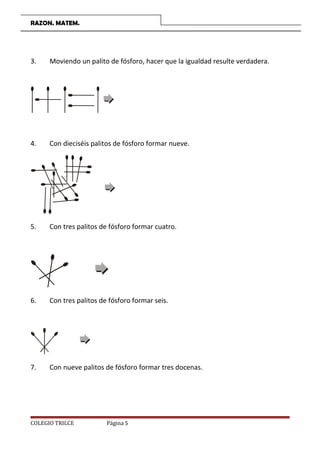
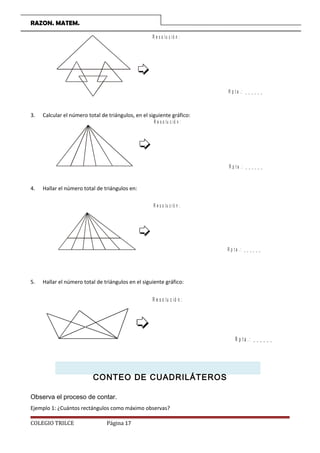
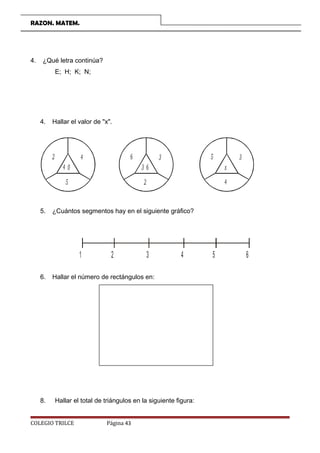
Este documento presenta varios problemas y ejercicios relacionados con el conteo de segmentos, figuras geométricas como triángulos y cuadriláteros. Instruye a los estudiantes sobre cómo resolver problemas de conteo de manera sistemática asignando letras a las partes de una figura y sumando los conteos simples y compuestos. También incluye acertijos lógicos y tareas para realizar en casa.

1. RAZ.
MATEMAT.
I BIM.
TRILCE PRIMARIA

2. RAZON. MATEM.
Í n d i c e
Pág.
......................................................Matemática recreativa 83
......................................................Conteo de segmentos 89
.............................................................Conteo de figuras 93
.............................................................................Repaso 99
.........................................Sucesiones y arreglos literales
103
....................................................................Sucesiones II
109
.................................................Distribuciones numéricas
113
...................................................................Repaso general
119
COLEGIO TRILCE Página 2

3. RAZON. MATEM.
¿ E s t á s p r e p a r a d o ? S Í N O
H o la c o m o e s t á s , b ie n v e n id o a e s t a h e r m o s a f a m ilia
T R I L C E , s e g u r o q u e e s t á s m u y c o n t e n t o , j u n t o s
d e s a r r o lla r e m o s e l c u r s o d e
d e u n a f o r m a d iv e r t id a y d id á c t ic a .
E l p r im e r t e m a e s M a t e m á t ic a R e c r e a t iv a n o n e c e s it a s
s a b e r f ó r m u la s c o m p lic a d a s , n i t e o r e m a s c o m p le j o s , s ó lo u n
p o c o d e in g e n io y h a b ilid a d .
R a z o n a m i e n t o M a t e m á t i c o
PROBLEMAS SOBRE PALITOS
1. Con doce palitos de fósforo se ha formado el siguiente arreglo:
COLEGIO TRILCE Página 3
Ahora resuelve los siguientes retos que se te
presentan a continuación:

4. RAZON. MATEM.
Primer Reto: Quita dos palitos de fósforo, de tal manera que queden sólo
dos cuadrados. ¡Vamos tú puedes!
Segundo Reto: Mover cuatro palitos de fósforo, de tal manera que formen
tres cuadrados iguales a los iniciales.
A h o r a d ic e m o v e r
y n o q u it a r o s a c a r
Reto Final: Moviendo cuatro palitos de fósforo, de la figura inicial formar diez
cuadrados.
N o d e b e n q u e d a r
p a lit o s s u e lt o s
2. Con diez palitos de fósforo formar uno.
COLEGIO TRILCE Página 4

5. RAZON. MATEM.
3. Moviendo un palito de fósforo, hacer que la igualdad resulte verdadera.
4. Con dieciséis palitos de fósforo formar nueve.
5. Con tres palitos de fósforo formar cuatro.
6. Con tres palitos de fósforo formar seis.
7. Con nueve palitos de fósforo formar tres docenas.
COLEGIO TRILCE Página 5

6. RAZON. MATEM.
8. Quitar cinco palitos de fósforo de tal manera que queden tres cuadrados
solamente.
9. Quitar dos palitos de fósforo, de tal manera que queden sólo dos cuadrados.
10. Mover dos palitos de fósforo de tal manera que el recogedor quede de la
misma forma pero el corazón fuera de él.
11. Con cinco palitos de fósforo, formar dos triángulos equiláteros.
ACERTIJOS LÓGICOS
COLEGIO TRILCE Página 6

7. RAZON. MATEM.
1. Tres osos van en fila india por un camino, adelante va el oso, le sigue la osa y luego
el osito; ¿cuál de los tres puede decir: Me siguen dos osos?
Rpta.: ________________
2. A una persona se le cayó su sombrero en una piscina; ¿cómo lo saca?
Rpta.: ________________
3. ¿Cómo se llama al último piso de un edificio de 20 pisos?
Rpta.: ________________
4. Si usted está frente a su lápida, ¿qué fecha le pondría?
Rpta.: ________________
5. Si una pata pone huevo exactamente en la línea límite entre el Perú y Chile, ¿a quién
pertenece el huevo?
Rpta.: ________________
TAREA DOMICILIARIA
1. Moviendo dos palitos de fósforo, cambiar el arreglo de la figura I, por el arreglo de la
figura II.
COLEGIO TRILCE Página 7

8. RAZON. MATEM.
I I I
2. ¿Cuántos palitos de fósforo debes mover como mínimo, para transformar la casa de
la figura I en la casa de la figura II?
I I I
Rpta.: _____________
3. Moviendo un palito de fósforo formar cuatro.
COLEGIO TRILCE Página 8

9. RAZON. MATEM.
Rpta.: _____________
4. Con cinco palitos de fósforo formar veintiuno.
Rpta.: _____________
5. En la figura, quitar cuatro palitos de fósforo para formar cinco cuadrados.
Rpta.: _____________
CARACTERÍSTICAS FÍSICAS:
I. ¿QUÉ ORDEN SIGO PARA COLOREAR?
COLEGIO TRILCE Página 9

10. RAZON. MATEM.
S e g m e n t o e s u n a p o r c ió n d e r e c t a y e s lim it a d a ,
e l s e g m e n t o A B s e d e n o t a a s í: A B
µ Ejemplo 1:
¿Cuántos segmentos, observas en la siguiente figura?
P R O F E
1 . A s ig n a m o s u n a le t r a m i n ú s c u la a
c a d a p a r t e .
2 . C o n t a m o s lo s s e g m e n t o s d e u n a
p a r t e ( s im p le s )
3 . C o n t a m o s s e g m e n t o s d e d o s p a r t e s
( c o m p u e s t o s )
4 . C o n t a m o s s e g m e n t o s d e t r e s p a r t e s
( c o m p u e s t o s )
5 . C o n t a m o s s e g m e n t o s d e c u a t r o
p a r t e s ( c o m p u e s t o s )
R e s o lu c ió n :
P
6 . H a ll a m o s la s u m a .
D e 1 p a r t e
D e 2 p a r t e s
D e 3 p a r t e s
D e 4 p a r t e s
a ; b ; c ; d
a b ; b c ; c d
a b c ; b c d
a b c d
T O T A L
4
3
2
1
1 0
N ° d e S e g m e n t o s
R O F E
a b c d
P R
a
R O
b
O F
c
F E
d
P R O
a b
R O F
b c
O F E
c d
P R O
a b
F
c
R O F
b c
E
d P R O F E
a b c d
Rpta.: El número total de segmentos es 10.
P r e g u n t a a t u p r o f e s o r s i n o h a y a lg ú n m é t o d o
c o r t o p a r a la r e s o lu c ió n d e e s t e p r o b le m a
Anota lo que tu profesor te diga.
COLEGIO TRILCE Página 10

11. RAZON. MATEM.
µ Ejemplo 2:
¿Cuántos segmentos hay en la siguiente figura?
R p t a . : _ _ _ _ _ _
A
B
C
D
E
G
H
F
EJERCICIOS PARA LA CLASE
1. ¿Cuántos segmentos hay como máximo?
R p t a . : _ _ _ _ _ _
A B C D E F
R e s o lu c ió n
2. Hallar el número total de segmentos en:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
J
Q
S
E
O
C
T
V
A
IP
3. Hallar el número total de segmentos en:
COLEGIO TRILCE Página 11

12. RAZON. MATEM.
R p t a . : _ _ _ _ _ _
R e s o lu c ió nHGFED
Ñ N M LA
B
C
K
J
I
4. Hallar el número total de segmentos.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
5. Hallar el número total de segmentos en la siguiente figura:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
6. Hallar el número total de segmentos en la siguiente figura:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
COLEGIO TRILCE Página 12

13. RAZON. MATEM.
7. ¿Cuántos segmentos hay en el siguiente gráfico?
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
TAREA DOMICILIARIA
1. Hallar el número total de segmentos en:
A B C D E
2. Hallar el número total de segmentos en:
E FC D
A
B
3. Hallar el número total de segmentos en:
COLEGIO TRILCE Página 13

14. RAZON. MATEM.
FGHIJK
E
D
CBA
N
M
L
4. Hallar el número total de segmentos en:
A M A B L E
H o la d e n u e v o a m i g u i t o y a l le g a m o s j u n t o s a l s e g u n d o
n iv e l ( t e m a ) . S a b ía s q u e l o s e j e r c ic i o s d e C o n t e o d e f ig u r a s
g e n e r a lm e n t e f o r m a n p a r t e d e t o d o s l o s e x á m e n e s
d e in g r e s o a lo s c e n t r o s d e e d u c a c ió n s u p e r i o r. N o p o r q u e
s e a n d i f íc il e s , s in o ; p o r q u e e v a lú a n e l n i v e l d e a n á li s is , d e
s ín t e s is y la c a p a c id a d d e a t e n c ió n y c o n c e n t r a c i ó n .
A s í q u e c o n c é n t r a t e y o b s e r v a t o d o l o q u e t u p r o f e s o r ( a )
d e s a r r o l l e e n l a p i z a r r a .
¿ E s t á s p r e p a r a d o ? S Í N O
CONTEO DE TRIÁNGULOS
Observa el proceso de contar.
Ejemplo 1: En la siguiente figura, ¿cuántos triángulos como máximo observas?
COLEGIO TRILCE Página 14

15. RAZON. MATEM.
1 . A s ig n a m o s u n a le t r a a c a d a u n a d e
la s f ig u r a s .
a b
c
d e
2 . C o n t a m o s lo s t r iá n g u l o s d e u n a
p a r t e ( s im p le s )
a b
c
d
3 . C o n t a m o s lo s t r iá n g u lo s d e d o s
p a r t e s ( c o m p u e s t o s )
a b
e
ba
c
4 . C o n t a m o s lo s t r iá n g u lo s d e t r e s
p a r t e s ( c o m p u e s t o s )
a
c
d
5 . C o n t a m o s lo s t r iá n g u lo s d e c in c o
p a r t e s ( c o m p u e s t o s )
a b
c
d e
6 . H a l la m o s la s u m a :
D e 1 p a r t e
D e 2 p a r t e s
D e 3 p a r t e s
D e 5 p a r t e s
a ; b ; c ; d
a c ; a b ; b e
a c d
a b c d e
T O T A L
4
3
1
1
9
N ° d e T r iá n g u lo s
R e s o lu c ió n :
A h o r a t e t o c a a t i.
Ejemplo 2:
¿Cuántos triángulos hay como máximo en la siguiente figura?
1
2
3
4
5
COLEGIO TRILCE Página 15

16. RAZON. MATEM.
P r e g u n t a a t u p r o f e s o r s i h a y
a lg ú n m é t o d o c o r t o p a r a
la s o lu c ió n d e e s t e p r o b le m a .
Anota lo que tu profesor te diga.
EJERCICIOS PARA LA CLASE
1. Calcular el máximo número de triángulos en el siguiente gráfico.
2. ¿Cuántos triángulos se pueden contar en la siguiente figura?
COLEGIO TRILCE Página 16
Resolución:
Rpta.: ______

17. RAZON. MATEM.
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
3. Calcular el número total de triángulos, en el siguiente gráfico:
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
4. Hallar el número total de triángulos en:
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
5. Hallar el número total de triángulos en el siguiente gráfico:
R e s o lu c ió n :
R p t a . : _ _ _ _ _ _
CONTEO DE CUADRILÁTEROS
Observa el proceso de contar.
Ejemplo 1: ¿Cuántos rectángulos como máximo observas?
COLEGIO TRILCE Página 17

18. RAZON. MATEM.
1 . S e a s ig n a u n a le t r a a c a d a p a r t e .
a
2 . C o n t a m o s lo s r e c t á n g u lo s d e u n a
s o la p a r t e .
3 . C o n t a m o s lo s r e c t á n g u lo s q u e s e
fo r m a n c o n d o s p a r t e s ( c o m p u e s t o s ) .
4 . C o n t a m o s lo s r e c t á n g u lo s q u e s e
f o r m a n c o n t r e s p a r t e s
H a y _ _ _ _ r e c t á n g u lo s
6 . C o n t e m o s e l t o t a l d e r e c t á n g u lo s .
1
2
3
a ; b ; c ; d ; e ; f
_ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _
T O T A L
_ _ _
_ _ _
_ _ _
_ _ _
N ° d e R e c t á n g u lo s
R e s o lu c ió n :
b c
d e
f
a
b c
d e
f
b
e
b c
d e
H a y _ _ _ _ r e c t á n g u lo s
a
b c
d e
f
H a y _ _ _ _ r e c t á n g u lo s
N ° d e Pa r t e s
EJERCICIOS PARA LA CLASE
1. ¿Cuántos cuadriláteros hay en el siguiente gráfico?
R p t a . : _ _ _ _ _ _
R e s o lu c i ó n
2. Hallar el número total de rectángulos en:
COLEGIO TRILCE Página 18

19. RAZON. MATEM.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
3. Hallar el número total de cuadrados en:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
4. Hallar el número total de cuadrados en la siguiente torre:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
5. Hallar el número total de rectángulos en:
R p t a . : _ _ _ _ _ _
R e s o lu c i ó n
TAREA DOMICILIARIA
COLEGIO TRILCE Página 19
1. ¿Cuántos cuadrados hay en el
siguiente gráfico?
2. ¿Cuántos triángulos hay?
3. ¿Cuántos rectángulos hay?
4. Hallar el número total de cuadriláteros en:
5. Hallar el número total de cuadrados en:

20. RAZON. MATEM.
Lee y completa:
COLEGIO TRILCE Página 20

21. RAZON. MATEM.
H o y h a r e m o s u n r e p a s o d e lo s t r e s t e m a s
q u e h e m o s v is t o h a s t a a h o r a .
S i n o h a z c o m p r e n d id o a lg u n o s
p r o b le m a s , lo h a r á s e n
e s t e r e p a s o . ¡ A P R O V É C H A L O !
EJERCICIOS
COLEGIO TRILCE Página 21
1. ¿Cuántas cifras se deben mover como
mínimo para formar una verdadera
igualdad?
13 - 32 = 4
2. En la siguiente figura añada dos palitos
para que dé cero.
3. ¿Cuántos palitos se deben mover como
mínimo para obtener una verdadera
igualdad?
4. ¿Cuántos palitos se deben quitar como
mínimo para obtener sólo cuatro
cuadrados iguales?
5. Quitar ocho palitos de la figura de tal
manera que queden dos cuadrados.
6. Coloca las cifras del 1 al 5 en los círculos
de la figura mostrada, (sin repetirlas) de
tal manera que la hilera vertical y
horizontal sumen lo mismo y ésta sea
igual a 9. ¿Cuál es la cifra que debe estar
en el círculo central?
7. Colocar las cifras del 1 al 9 en los círculos de
la figura mostrada, (sin repetirlos) de tal
manera que todas las hileras formadas por
tres círculos sumen lo mismo y ésta sea igual
a 12. ¿Cuál es la cifra que debe estar en el
círculo central?
= 1 2
=
1 2
=
12
=12
8. ¿Cuántos segmentos hay en la siguiente
figura?
9. Hallar el número total de triángulos que hay
en la siguiente figura:
10. ¿Cuántos segmentos hay en la
siguiente figura?
A
L
U
M
N
O
T
R
I
L
C
E
T R I U N F A
11. ¿Cuántos triángulos hay en la siguiente
figura?
12. ¿Cuántos segmentos hay en la
siguiente figura?
13. ¿Cuántos triángulos hay en la siguiente
figura?

22. RAZON. MATEM.
COLEGIO TRILCE Página 22
14. Hallar el número total de triángulos en la
figura mostrada:
15. ¿Cuántos triángulos hay en el gráfico
mostrado?

23. RAZON. MATEM.
TAREA DOMICILIARIA
COLEGIO TRILCE Página 23
1. Con trece palitos de fósforo, formar cuatro
cuadrados iguales.
2. ¿Cuántos palitos se deben quitar como
mínimo, para que queden sólo cinco
cuadrados iguales?
3. ¿Cuántas cifras se deben mover como
mínimo para formar una verdadera
igualdad?
32 - 23 = 1
4. ¿Cuántos triángulos hay en la siguiente
figura?
5. ¿Cuántos segmentos hay en la siguiente
figura?

24. RAZON. MATEM.
Q u e r id o s a m i g o s , e l t e m a q u e d e s a r r o lla r e m o s
h o y e s u n o d e m is f a v o r it o s ; y o s é q u e t a m b i é n
s e r á d e t u a g r a d o , m e r e f ie r o , a l t e m a d e
S u c e s io n e s y A r r e g lo s L it e r a le s ,
p e r o ¿ q u é e s u n a s u c e s ió n ? . V e a m o s e l c o n c e p t o
SUCESIÓN
Es un conjunto ordenado de números de acuerdo a una ley de formación. Dichos números
son los términos de la sucesión.
P o r e j e m p lo , e l s ig u ie n t e c o n j u n t o o r d e n a d o d e n ú m e r o s :
1 ; 3 ; 5 ; 7 ; 9 ; . . . t ie n e u n a le y d e f o r m a c ió n .
En efecto, si aumentamos en dos unidades a cada uno de los números, obtendremos el
siguiente.
Por lo tanto: (1; 3; 5; 7; 9; . . . ) es una SUCESIÓN, donde los términos mantienen un
orden y se les nombra del modo siguiente:
1: primer término
3: segundo término
5: tercer término
7: cuarto término, etc.
A h o r a v e a m o s o t r a s u c e s ió n : 5 ; 7 ; 1 0 ; 1 4 ; . . .
¿ P o d r ía s h a lla r e l t é r m in o q u e s i g u e ?
Para resolver este problema, debemos encontrar la ley de formación, como se muestra a
continuación:
COLEGIO TRILCE Página 24

25. RAZON. MATEM.
5 ; 7 ; 1 0 ; 1 4 ; . . .
+ 2 + 3 + 4 + 5
Por lo tanto el número que sigue deberá ser: 14 + 5; esto es 19.
ARREGLOS LITERALES
Es un conjunto ordenado de letras de acuerdo a un determinado criterio. Para encontrar el
criterio de ordenamiento de las letras en un problema dado, es necesario conocer bien el
abecedario, tener en cuenta la posición de cada letra y no se debe considerar las letras
compuestas CH y LL.
P o r e j e m p lo : ¿ Q u é le t r a s ig u e ?
A ; C ; F ; J ; . . .
Este arreglo tiene cierto criterio de ordenamiento. En efecto, observemos lo siguiente:
A ; C ; F ; J
B D E G H I
Entre A y C hay una letra intermedia;
entre C y F hay dos letras intermedias;
entre F y J hay tres letras intermedias.
Por lo tanto entre J y la letra que sigue deben haber cuatro letras intermedias.
A ; C ; F ; J ; . . .
B D E G H I K L M N
Entonces la letra que sigue es: ______
Nota: Se puede resolver el problema anterior de otra manera, lo único que necesitamos saber es, la
posición que ocupa cada letra del arreglo dado, en el abecedario.
COLEGIO TRILCE Página 25

26. RAZON. MATEM.
A
1
B C D E F G H I J K L M N
2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4
Ñ
1 5
O P Q R S T U V W X Y Z
1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7
R e c u e r d a q u e n o s e c o n s id e r a n l a s le t r a s
c o m p u e s t a s C H y L L e n a r r e g lo s lit e r a le s .
Ahora observa como se resuelve el problema anterior pasando del arreglo literal a una
SUCESIÓN
A ; C ; F ; J ; . . .
1 ; 3 ; 6 ; 1 0 ; . . .
P o s ic ió n e n
e l a b e c e d a r io
+ 2 + 3 + 4 + 5
Ñ
1 5
Como verás, el número que sigue en la sucesión es 15, ahora sólo tenemos que buscar
la letra que ocupa la posición número 15 en el abecedario y ésta es la letra Ñ.
¡ A h o r a h a z lo T ú !
¿ Q u é le t r a s ig u e e n e l s ig u ie n t e a r r e g lo lit e r a l?
C ; F ; J ; M ; P ; . . .
C ; F ; J ; M ; P ; . . .
R p t a . : _ _ _ _ _ _ _
EJERCICIOS PARA LA CLASE
I. Encontrar el número que sigue en cada una de las siguientes sucesiones:
COLEGIO TRILCE Página 26

27. RAZON. MATEM.
II. Encontrar la letra que sigue en cada uno de los siguientes arreglos
literales:
COLEGIO TRILCE Página 27
1) 2; 4; 6; . . .
2) 18; 15; 12; . . .
3) 2; 4; 8; 16; . . .
4) 24; 12; 6; . . .
5) 22; 18; 13; 7; . . .
6) 2; 4; 8; 14; . . .
7) 5; 3; 6; 4; 8; 6; 12; . . .
8) 1; 1; 2; 6; . . .
9) 1; 2; 4; 8; 10; . . .
10) 2; 3; 4; 5; 8; 7; 16; . . .
1) A; D; G; J; . . .
2) B; D; G; I; L; . . .
3) C; E; I; Ñ; . . .
4) A; B; D; D; G; F; J; . . .
5) B; C; E; H; L; . . .

28. RAZON. MATEM.
TAREA DOMICILIARIA
I. Hallar el número que sigue en cada una de las siguientes
sucesiones:
1) 2; 7; 14; 23; . . .
2) 2; 6; 4; 12; 10; 30; . . .
3) 1; 1; 3; 3; 9; 5; 27; . . .
4) 2; 5; 7; 10; 12; 15; . . .
5) 2; 3; 6; 7; 14; 15; . . .
II. Hallar la letra que sigue en cada uno de los siguientes arreglos
literales:
COLEGIO TRILCE Página 28

29. RAZON. MATEM.
1) A; C; B; D; C; E; . . .
2) B; D; F; H; . . .
3) C; E; H; J; M; . . .
4) A; Z; D; W; G; T; . . .
5) A; B; D; H; . . .
R e s u e lv e t u s e j e r c ic io s
c o n O R D E N y lim p ie z a .
E n e s t e c a p ít u lo v e r e m o s u n a g r a n v a r ie d a d
d e s u c e s io n e s y t e n e m o s q u e e n c o n t r a r la l e y
d e f o r m a c ió n d e c a d a u n a d e e lla s , p a r a lu e g o
h a lla r la q u e n o s p id e n .
EJERCICIOS PARA LA CLASE
COLEGIO TRILCE Página 29

30. RAZON. MATEM.
I. Hallar el número que sigue en cada sucesión:
1 . 5 ; 9 ; 7 ; 1 1 ; 9 ; . . . .
2 . 1 ; 1 ; 2 ; 4 ; 7 ; 1 1 ; . . . .
3 . 2 6 ; 1 8 ; 1 1 ; 5 ; . . . .
4 . 1 ; 1 ; 3 ; 7 ; . . . .
5 . 3 ; 4 ; 8 ; 1 1 ; 1 2 ; 2 4 ; 2 7 ; . . . .
II. Hallar el valor de x + y en cada una de las siguientes sucesiones:
COLEGIO TRILCE Página 30

31. RAZON. MATEM.
1 . 1 ; 1 ; 5 ; 2 ; 9 ; 4 ; 1 3 ; x ; y ; . . . .
2 . 3 ; 6 ; 9 ; 1 8 ; 2 1 ; x ; y ; . . . .
3 . 1 ; 3 ; 4 ; 1 2 ; 1 3 ; x ; y ; . . . .
4 . 2 ; 4 ; 9 ; 1 8 ; 2 3 ; x ; y ; . . . .
5 . 8 ; 9 ; 1 1 ; 1 5 ; 2 2 ; x ; y ; . . . .
TAREA DOMICILIARIA
1. ¿Qué número sigue?
2; 3; 5; 10; 8; 17; . . . .
Rpta.: _____________
COLEGIO TRILCE Página 31

32. RAZON. MATEM.
2. Hallar x + y en:
66; 60; 30; 24; 12; x; y; . . . .
Rpta.: _____________
3. ¿Qué número sigue?
2; 2; 4; 12; . . .
Rpta.: _____________
4. Hallar x + y en:
5; 6; 4; 12; 13; 11; x; y; . . . .
Rpta.: _____________
5. ¿Qué número sigue?
1; 1; 4; 12; 27; . . . .
Rpta.: _____________
COLEGIO TRILCE Página 32

33. RAZON. MATEM.
O b s e r v a c o m o s e h a n d is t r ib u id o lo s n ú m e r o s e n
c a d a u n a d e la s s ig u ie n t e s f ig u r a s :
1 9
4 2
2 1 7
3 5
5 x
6 3
¿ P o d r ía s h a lla r e l v a lo r d e x ?
Claro que sí, sólo tenemos que buscar la relación que existe entre los
demás números dados.
Veamos:
- De la primera figura tenemos que: 4 × 2 + 1 = 9 y
de la segunda figura tenemos que: 3 × 5 + 2 = 17
Como verás se ha encontrado una misma relación para las dos primeras
figuras y esa relación se debe dar también en la tercera figura.
Por lo tanto; de la tercera figura tenemos que: x = 6 × 3 + 5.
Es decir el valor de x es 23
A h o r a v e a m o s u n a d is t r ib u c ió n lit e r a l:
A B
F
C
C D
L
E
E F
?
G
¿ Q u é le t r a f a lt a ?
COLEGIO TRILCE Página 33

34. RAZON. MATEM.
Para resolver este problema, sólo basta con reemplazar cada una de las letras con
los números que indican la posición de éstas en el abecedario.
Así tenemos:
1 2
6
3
3 4
1 2
5
5 6
?
7
- De la primera figura se tiene que: 1 + 2 + 3 = 6 y
de la segunda figura se tiene que: 3 + 4 + 5 = 12
Por lo tanto; en la tercera figura el número que falta es: 5 + 6 + 7; esto es 18.
Entonces tenemos que buscar la letra número 18 en el abecedario y ésta es la letra
Q.
EJERCICIOS PARA LA CLASE
I. Hallar el valor de x en cada una de las siguientes distribuciones
numéricas:
1 ) 4
2
3
1 2
1 4
x
3
7
5
R p t a . : _ _ _ _ _
COLEGIO TRILCE Página 34
3 ) 1 3
x
1 0
8
3
5
1 9
8
1 1
R p t a . : _ _ _ _ _
4 ) 1 2
4
3
1 8
3
6
2 0
2
x
R p t a . : _ _ _ _ _

35. RAZON. MATEM.
2 ) 5
3
9
9
1 1
x
4
8
7
R p t a . : _ _ _ _ _
5 ) 4
7
5
5
1
2
2
3
x
R p t a . : _ _ _ _ _
6 ) 3
6
2
1 6
1 3
x
5
2
8
R p t a . : _ _ _ _ _
7 ) 4
2
5
8
3
5
6
2
2
4
1 0
5
1 0
6
2 0
x
R p t a . : _ _ _ _ _
8)
2 3
9
3
5 3
1 7
2
7 4
x
5
Rpta.: _______
COLEGIO TRILCE Página 35

36. RAZON. MATEM.
9)
32
1 0
14
25
1 6
23
53
x
25
Rpta.: _______
10)
1 2 3
6
4 4 5
8 0
1 5 7
x
Rpta.: _______
II. Hallar la letra que falta en cada una de las siguientes distribuciones
literales:
1)
B C
A
D
D G
C
H
F D
E
?
Rpta.: _______
2)
D B
A G
C A
F J
F E
B ?
COLEGIO TRILCE Página 36

37. RAZON. MATEM.
Rpta.: _______
3)
B
K
A
A G
H
S
C
E D
A
?
D
E J
Rpta.: _______
4 ) B
E
G
H
Ñ
?
D
C
C
R p t a . : _ _ _ _ _
5 ) B
C
E
C
D
A
G
M
?
R p t a . : _ _ _ _ _
TAREA DOMICILIARIA
I. Hallar el valor de x en cada caso:
1 ) 2
3
1
8
9
5
5
6
x
R p t a . : _ _ _ _ _
2 ) 3
4
1 2
7
2
1 4
9
3
x
R p t a . : _ _ _ _ _
3 ) 1 8
7 2
4 3
1 3
1 1
x
3 1
1 1
2 8
R p t a . : _ _ _ _ _
II. Hallar la letra que falta en cada caso:
4)
COLEGIO TRILCE Página 37

38. RAZON. MATEM.
B E
F
D
D B
A
G
J A
?
B
Rpta.: _________
5)
J
C D
H
B E
?
F B
Rpta.: _________
1. Completa según convenga:
C o m o e s t á n a m ig u it o s , e s t a e s n u e s t r a ú lt im a c la s e
d e l p r im e r b im e s t r e , s ie n t o u n a in m e n s a a le g r ía a l
s a b e r q u e h a z a p r e n d id o m u c h o .
H o y r e p a s a r e m o s lo s t e m a s d e : M a t e m á t ic a R e c r e a t iv a ,
C o n t e o d e F ig u r a s I y I I , S u c e s io n e s I y I I y D is t r ib u c io n e s .
T ie n e s q u e a p r o v e c h a r e s t e r e p a s o a l m á x im o , p u e s
y a s e v ie n e e l e x a m e n b im e s t r a l. ¿ N e r v io s o ( a ) ? n o t e
p r e o c u p e s q u e y o t e a c o m p a ñ o .
PROBLEMAS
1. Puedes quitar seis dígitos del siguiente arreglo para que te dé un total de 20.
COLEGIO TRILCE Página 38

39. RAZON. MATEM.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
1
7
9
1
7
9
1
7
9
2. Se tiene la siguiente cantidad de palitos de fósforo.
¿Podrías transformar los 16 palitos de fósforo en nueve sin quitar ninguno de ellos? Además
no puedes superponerlos.
2. ¿Cuántos triángulos hay en el siguiente gráfico?
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
3. Hallar el número total de triángulos que tengan una en su interior.
COLEGIO TRILCE Página 39

40. RAZON. MATEM.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
5. Hallar el número total de segmentos en el siguiente gráfico:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
6. Hallar el número total de cuadrados en el siguiente gráfico:
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
7. Hallar el número total de rectángulos.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
8. Hallar el número total de cuadriláteros.
COLEGIO TRILCE Página 40

41. RAZON. MATEM.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
9. Hallar el número total de segmentos.
R p t a . : _ _ _ _ _ _
R e s o lu c ió n
O
GIMA
T
R
I
L
C
E
T
U
10. ¿Qué números siguen en las siguientes sucesiones?
1; 5; 2; 10; 3; 15; 4; ; ; . . .
2; 4; 7; 12; 20; ; ; . . . .
Rpta.: _______
11. ¿Qué letras siguen en el siguiente arreglo literal?
C; E; G; I; ; ; . . . .
Rpta.: _______
COLEGIO TRILCE Página 41
12. ¿Qué número falta?
18 (48) 30 →
12 (30) 18 →
16 ( ) 20 →
Rpta.: ____________
13. ¿Qué número falta?
16 (9) 7 →
28 (16) 12 →
34 ( ) 14 →
14. Hallar el valor de x
3 8 2 →
1 2 10 →
4 4 x →
Rpta.: ____________
15. Hallar el valor de x
5 3 1 →
2 4 1 →
1 1 x →

42. RAZON. MATEM.
TAREA DOMICILIARIA
1. ¿Cuántos palitos se deben quitar como mínimo para que queden sólo cuatro cuadrados
iguales?
2. Hallar el número total de triángulos.
3. ¿Qué número sigue en la siguiente sucesión?
6; 12; 8; 10; 10; 8; . . . . .
COLEGIO TRILCE Página 42

43. RAZON. MATEM.
4. ¿Qué letra continúa?
E; H; K; N;
4. Hallar el valor de x.
2 4
4 0
5
6 3
3 6
2
5 3
x
4
5. ¿Cuántos segmentos hay en el siguiente gráfico?
1 2 3 4 5 6
6. Hallar el número de rectángulos en:
8. Hallar el total de triángulos en la siguiente figura:
COLEGIO TRILCE Página 43

44. RAZON. MATEM.
9. ¿Qué número sigue?
1; 2; 4; 7; 11; . . .
10. ¿Qué número falta?
5
1 1
1 2
1 3
0 1
4 8
?
4 4
1 1
COLEGIO TRILCE Página 44