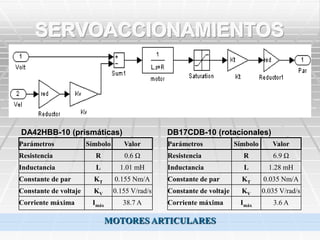
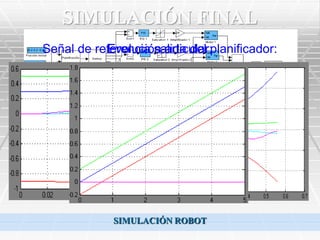
Este documento describe el diseño de un robot quirúrgico. Explica la cinemática directa e inversa del robot, incluyendo la matriz jacobiana. También cubre la dinámica directa e inversa mediante el uso de las ecuaciones de Newton-Euler. Finalmente, selecciona servomotores adecuados para cada articulación basándose en los pares máximos requeridos.





![CINEMÁTICA INVERSA
function q = inversa(T)
l4=0.4;
l5=0.2;
% Inicialización de las variables articulares a calcular
q=[0 0 0 0 0];
% Solución de las articulaciones
q(1)=T(1,4)-l5*T(2,1)*T(3,2);
q(2)=T(2,4)+l5*T(1,1)*T(3,2);
q(3)=-T(3,4)-l4+l5*T(3,3);
q(4)=asin(T(1,1));
q(4)=atan2(T(1,1),T(2,1));
q(5)=asin(-T(3,3));
q(5)=atan2(-T(3,3),T(3,2));
CÓDIGO IMPLEMENTADO PARA LA CINEMÁTICA INVERSA
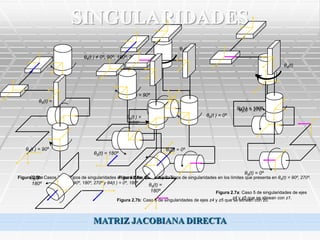
RESOLUCIÓN DEL PROBLEMA CINEMÁTICO INVERSO](https://image.slidesharecdn.com/robotquirrgico-121125030107-phpapp02/85/Robot-quirurgico-9-320.jpg)





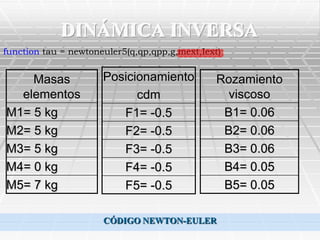



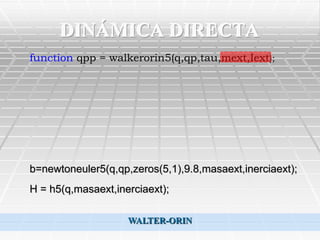
![DINÁMICA DIRECTA
Vector de aceleración de la gravedad
Vector de aceleración de la gravedad
Inicialmente [-g,0,0]
Finalmente [0,0,-g]
D-H 1ª articulación
CÓDIGO NEWTON-EULER](https://image.slidesharecdn.com/robotquirrgico-121125030107-phpapp02/85/Robot-quirurgico-22-320.jpg)