El documento describe un proyecto de innovación docente en la Universidad Autónoma de Madrid que utiliza el software Derive 5 para la enseñanza de matemáticas en las facultades de Ciencias Económicas y Empresariales. Se presentan los objetivos del curso que incluyen el desarrollo de contenidos matemáticos y la aplicación de soluciones a problemas mediante el uso de la programación. Se organizan las prácticas en módulos que abarcan desde la introducción al software hasta temas avanzados de cálculo diferencial e integral, así como álgebra lineal.










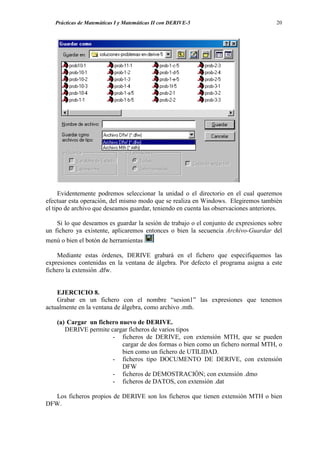
![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 12
es decir, como un conjunto de siete variables. Si queremos introducir una variable
que tenga por nombre la palabra formada por esos siete caracteres deberemos
aplicar la secuencia de comandos Definir Preferencias de entrada y seleccionar en
el campo Modo la opción Palabras
en este momento aparecerá en la última expresión de la ventana de álgebra de
DERIVE la expresión
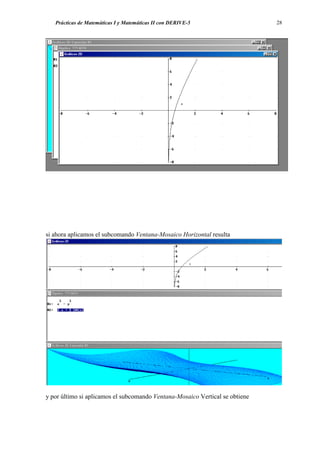
si ahora intentamos introducir la misma expresión anterior "ejemplo" obsérvese
que ahora sí queda introducida como una variable
4) DERIVE reconoce un conjunto de funciones matemáticas que tienen una
sintaxis especial. Algunas de las funciones matemáticas que se suelen utilizar
son las siguientes:
Funciones trigonométricas: sin(x), cos(x), tan(x),...
Funciones trigonométricas inversas: asin(x), acos(x), atan(x)...
Funciones logarítmicas: ln(x), log(x,a) (log. Neperiano, logaritmo de
x en base a)
Funciones exponenciales y radicales: sqrt(x) (raiz cuadrada), exp(x)
(exponencial de x).
Algunas otras funciones: abs(x) (módulo de x), x! (factorial de x),
int(x), parte entera de x
5) También existen algunas funciones predefinidas que sirven para efectuar
algunas operaciones matemáticas o utilizar expresiones matemáticas muy
comunes:
Algunas de estas funciones son:
IDENTITY_MATRIZ(n): con la que se obtiene una matriz identidad
de orden n. Por ejemplo si editamos “identity_matriz(3)” y
simplificamos esta expresión se obtiene
GRAD(funcion,variables): con la que se puede obtener el vector
gradiente de una “función” dada con las “variables” señaladas. Por
ejemplo editando “grad(x^2+y^2,[x,y])” se obtiene al simplificar](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-14-320.jpg)







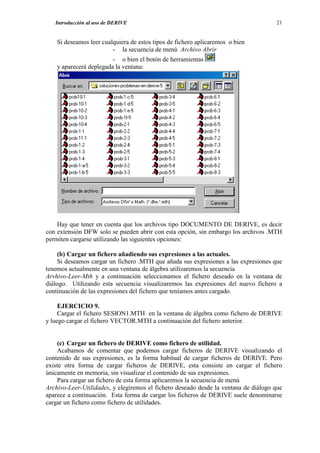

























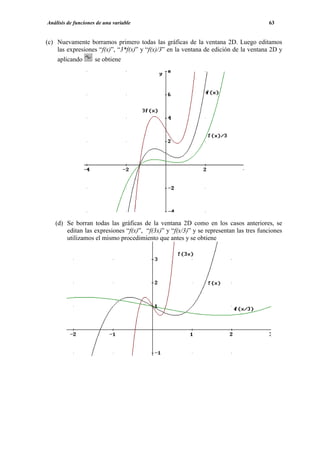
![Análisis de funciones de una variable 55
• DOMINIO.
Para estudiar el dominio se buscan los valores de x para los cuales f(x) es un número
real, o, si se utiliza la representación anterior, los valores de x para los cuales “hay
gráfica”. Obsérvese que en nuestro ejemplo, para x=2 y x=-2, no existe la función, ya que
estos son justamente los valores que anulan el denominador.
• RANGO.
Gráficamente el rango de la función es el conjunto de números del eje OY en los que
“existe la gráfica”. Como puede verse, en este caso el rango de la función es todo el
conjunto de números reales menos el intervalo (0,2] es decir en R(0,2].
• ASÍNTOTAS.
Asíntotas verticales. La función, como se ve gráficamente, tiene dos asíntotas
verticales, las rectas x=2 y x=-2. Analíticamente, para determinar las asíntotas verticales
x2 x2
estudiamos los siguientes límites lim+ 2 y lim− 2 . Para calcular el primer límite,
x → −2 x − 4 x → −2 x − 4
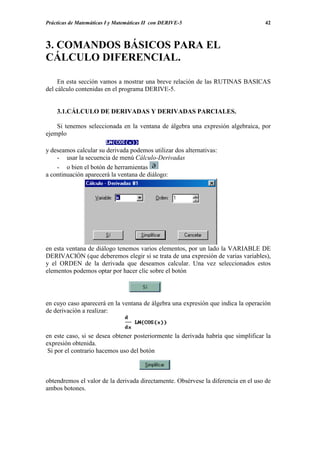
se edita la expresión “x^2/(x^2-4)”, se elige el botón de herramientas y en la ventana
de diálogo correspondiente al cálculo de límites se introducen la variable “x”, el punto -2 y
en el campo “Aproximación desde” se elige la opción “derecha”. Finalmente se hace clic
en y obtenemos
que tras simplificar con se obtiene
Es decir cuando x se aproxima a –2 por la derecha la rama de la gráfica se va -∞.
Para calcular el segundo límite se repite el proceso anterior, pero en el campo
“Aproximación desde” se elige la opción “izquierda” y obtenemos las expresiones
se observa que cuando los valores de x se aproximan a –2 por la izquierda la rama de la
gráfica se va a infinito.
Asíntotas horizontales. Gráficamente se ve que la recta y=1 es la única asíntota
horizontal de la función. Obsérvese que analíticamente los siguientes límites nos informan
de la existencia de dicha asíntota.](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-57-320.jpg)





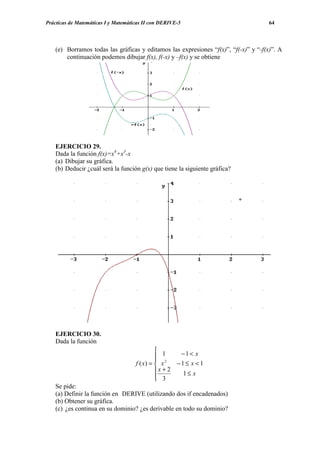
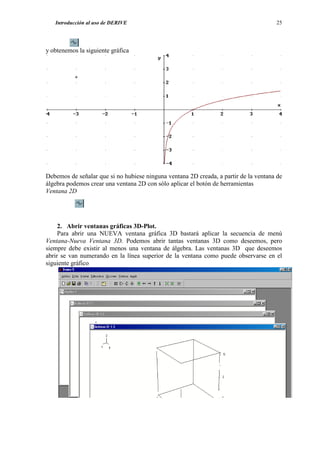
![Prácticas de Matemáticas I con DERIVE-5 66
5. ANÁLISIS DE FUNCIONES DE VARIAS
VARIABLES.
En este apartado trabajaremos con funciones de dos variables, aunque los cálculos
analíticos se pueden efectuar con funciones de más de dos variables, con las limitaciones
relacionadas con la imposibilidad de representar sus gráficas.
5.1. GRÁFICAS Y CURVAS DE NIVEL DE FUNCIONES DE DOS VARIABLES.
EJEMPLO 5.1.
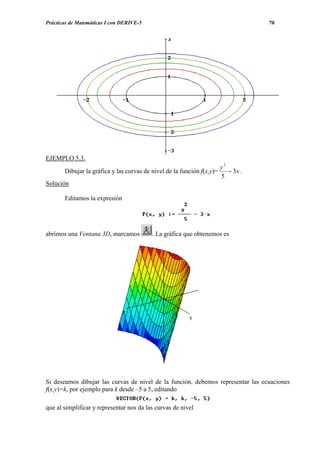
Dibujar la gráfica de la función
x2 + y2
cos
4
f ( x, y ) = .
2 2
3+ x + y
Solución
Editamos la función
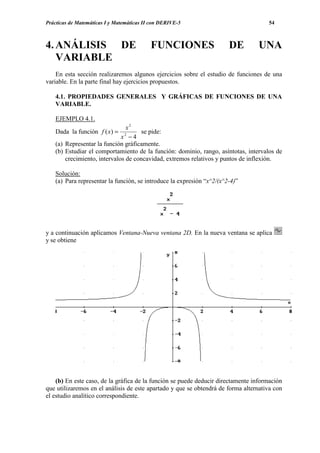
y marcamos en Ventana la opción Nueva ventana 3D o y una vez abierta la ventana 3D
marcamos nuevamente y obtenemos
Como el recorrido de la función coseno es [-1,-1], el recorrido de nuestra función es
[-1/3,1/3]. Modificamos, por tanto, la escala en la variable z, para obtener una mejor visión de
la gráfica. Marcamos y fijamos el mínimo de la variable z en –0.5 y el máximo en 0.5,
obteniendo](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-68-320.jpg)











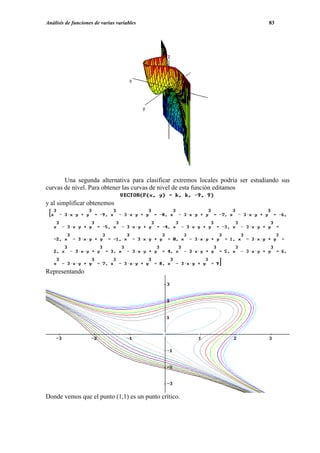

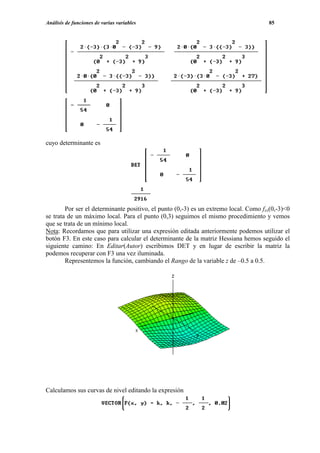

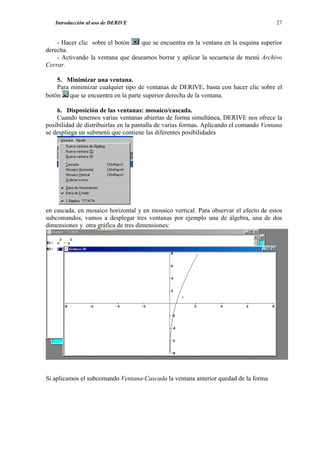
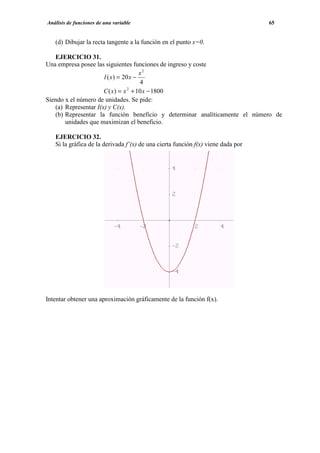
![Cálculo Integral 87
6. CÁLCULO INTEGRAL.
6.1. LA INTEGRAL DEFINIDA DE RIEMANN: UNA APROXIMACIÓN CON
DERIVE.
La integral definida de Riemann surge a partir del problema del cálculo de áreas de
superficies limitadas por curvas.
En el desarrollo del concepto de función integrable de una función acotada definida en
un intervalo acotado, aparecen los conceptos de integral superior e integral inferior de
Riemann. La idea consiste en efectuar aproximaciones por exceso y por defecto utilizando
los rectángulos exteriores e interiores a la curva, en función de una determinada partición
del intervalo.
Para efectuar esta práctica vamos a cargar el fichero RIEMANN.MTH mediante la
secuencia de comandos Archivo-Leer-Utilidad, tal como se explicó en la primera parte
sobre el manejo de ficheros con DERIVE.
Consideremos una función cualquiera, por ejemplo f(x)=x2, definida en el intervalo
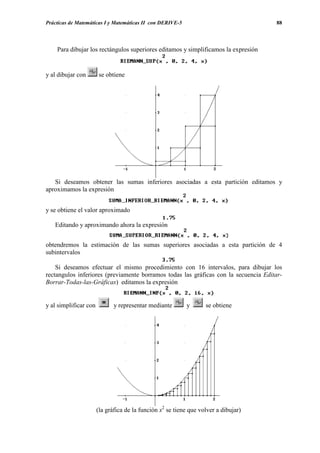
[0,2]. Una vez abierta una ventana 2-D con el botón , representamos esta función con
el botón de en la ventana 2D. Supongamos que efectuamos una partición del intervalo
[0,2] en 4 subintervalos. Si deseamos dibujar los rectángulos inferiores, basta que editemos
la expresión
y la simplifiquemos (obsérvese que _ es el subrayado).
Antes de dibujar los rectángulos es conveniente efectuar dos operaciones previas:
1. Indicar que el dibujo una sucesivamente los puntos que se van representando.
Para ello, una vez situados en la ventana 2D, con el comando Opciones-
Pantalla-Puntos debemos marcar la opción Unir-SI. Con esto se consigue que
se dibujen correctamente los rectángulos.
2. Indicar a DERIVE que dibuje sólo en un color, para que los rectángulos resulten
homogéneos. Esto se consigue desmarcando la opción Opciones-Cambio-de-
color. De esta forma todas las gráficas se dibujaran en un solo color.
A continuación ya podemos aplicar y obtenemos](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-89-320.jpg)
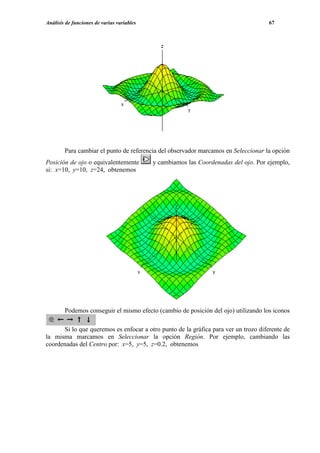
![Cálculo Integral 89
Para dibujar los rectángulos superiores basta editar
y representar la expresión obtenida al simplificar la anterior, obteniéndose
También podríamos obtener las sumas inferiores asociadas a esta partición
y las sumas superiores
Obsérvese que los valores de las sumas superiores van disminuyendo y los de las sumas
inferiores van aumentando.
Para calcular la integral superior de Riemann efectuamos un paso al límite. Su cálculo
se puede implementar en DERIVE definiendo la siguiente expresión
y lo mismo para la integral superior de Riemann
De tal forma que si deseamos calcular la integral inferior de Rieman de la función x2 en
el intervalo [0,2], basta editar la expresión
que al simplificar nos da
Para el cálculo de la integral superior de Riemann editamos
y se obtiene el mismo valor](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-91-320.jpg)
![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 90
Luego se puede afirmar (bajo ciertas condiciones de la función f(x)) que la función es
integrable. De hecho, si hubiésemos efectuado el cálculo de la integral definida de forma
directa con DERIVE hubiésemos obtenido el mismo resultado:
6.2. FUNCIÓN INTEGRAL DE UNA FUNCIÓN INTEGRABLE.
EJEMPLO 6.1.
Dada la función
2x 0 ≤ x ≤ 1
f ( x) =
x + 2 1< x
(a) Representar la función f(x)
(b) Calcular la función integral F(x) de f en [0,3].
(c) Representar gráficamente las dos funciones f(x) y F(x)
(d) ¿Es continua la función integral en [0,3]? ¿Es derivable en [0,3]?
(e) La función f(x) ¿tiene una primitiva en [0,3]?
Solución.
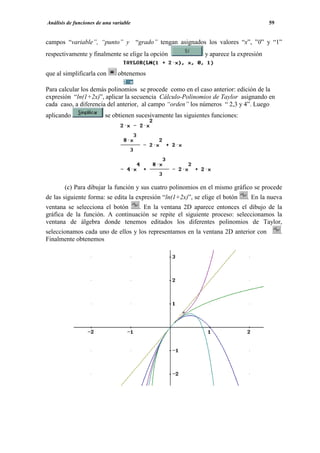
(a) Para representar f(x), vamos a definirla editando “f(x):=if(x≥0,if(x≤1,2x,x+2))” y se
obtiene la expresión:
A continuación aplicamos NuevaVentana2D y luego representamos con y
obtenemos la gráfica
(b) Como puede observarse en la gráfica, f(x) es continua salvo en x=1, por tanto es
integrable Riemann y en consecuencia existe su función integral.](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-92-320.jpg)
![Cálculo Integral 91
Para calcular la función integral debemos calcular dos integrales definidas, en
función de x. Si x∈[0,1], tendremos que calcular la integral definida
que al simplificar resulta
Por otro lado si x>1 debemos calcular
1 x
∫ 2tdt + ∫ (t + 2)dt
0 1
Es decir, construimos en primer lugar en DERIVE
en segundo lugar la integral
y a partir de ellas construimos la suma de ambas
que al simplificar resulta
Por tanto
2
0 ≤ x ≤1
2 x
F ( x) = x 3
2 + 2x − 2
1≤ x
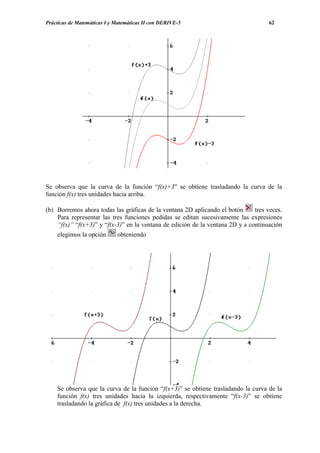
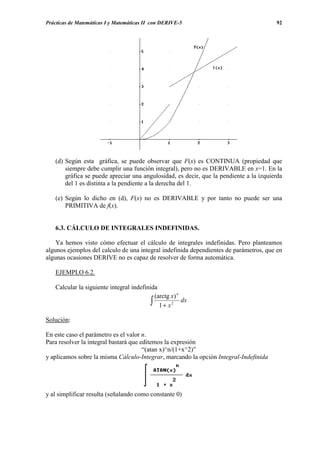
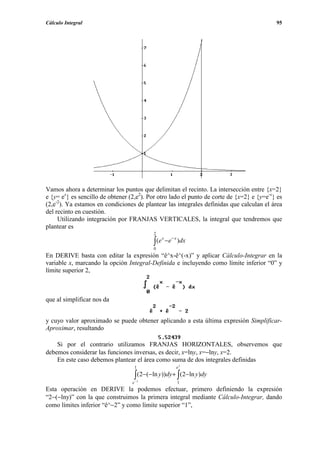
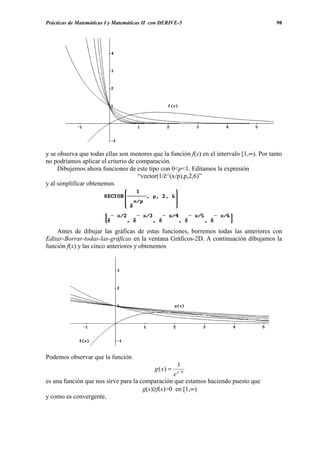
(c) Para representar ahora F(x), junto a f(x), editamos la función integral mediante la
expresión “f_integral(x):=if(x≥0,if(x≤1,x^2,x^2/2+2x-3/2))” y a continuación
aplicamos y representamos con obteniéndose](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-93-320.jpg)







![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 102
al finalizar aparece en la ventana de álgebra la expresión
(b) El segundo método consiste en editar la matriz como un vector de vectores fila.
En consecuencia editando
y al pulsar (enter) obtenemos nuevamente la expresión anterior.
• Dar nombre a un vector o a una matriz.
En general, lo más operativo en álgebra matricial suele ser el dar nombre a la matriz
o vector que hemos introducido utilizando la sintaxis:
(Nombre de vector o matriz) := (matriz o vector)
EJEMPLO 7.3.
Definir los vectores u=(3,5,6,-3) , v=(4,3,-9,-8).
Solución.
Para editar directamente vectores en DERIVE basta con introducir las componentes
entre corchetes, así para editar el primer vector introducimos la expresión
“u:=[3,5,6,-3]”
el segundo se obtiene escribiendo
“v:=[4,3,-9,-8]”
lo cual en DERIVE se muestra como
EJEMPLO 7.4.
Definir en DERIVE las matrices cuadradas dadas por
1 3 5 2 4 5
A = 2 − 2 1 B = 1 − 2 1
1 5 1 3 1 1
](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-104-320.jpg)

![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 104
Solución.
En primer lugar, definamos los vectores del problema escribiendo las expresiones
“u:=[1,3,4,-9]” y “v:=[2,0,3,4]”
(a) La suma se obtiene editando “u+v” y simplificando
(b) La diferencia se calcula editando “u-v” de tal forma que al simplificar resulta
(c) El producto escalar se obtiene mediante “u.v”
(d) La norma del vector u se obtiene editando y simplificando “abs(u)”
de igual forma se calcula la norma de v
(e) Editando “3u-5v”, al simplificar se obtiene el vector deseado
(f) Mediante la edición de “element(u,3)” tras simplificar resulta
(g) Aplicamos el comando Editar(Autor) e introducimos la expresión
“append(u,v)” que al simplificar nos da
7.3. OPERACIONES CON MATRICES.
Dadas dos matrices A y B, en DERIVE se pueden realizar las siguientes
operaciones, sin más que editar la expresión indicada y simplificar:
(a) SUMA DE DOS MATRICES “A+B”
(b) DIFERENCIA DE DOS MATRICES “A-B”
(c) PRODUCTO DE MATRICES “A.B”
(d) TRANSPUESTA DE UNA MATRIZ “A`” ¡ojo es el acento grave `! (este
símbolo se puede introducir o bien a través del teclado o bien a través de los
símbolos que aparecen en la ventana de edición )
(e) PRODUCTO DE UNA MATRIZ POR UN ESCALAR “α.A”
(f) DETERMINANTE DE UNA MATRIZ CUADRADA “det(A)”
(g) TRAZA DE UNA MATRIZ CUADRADA “trace(A)”
(h) INVERSA DE UNA MATRIZ NO SINGULAR “A^(-1)”
(i) INTRODUCCION DE MATRIZ IDENTIDAD DIMENSION N
“identity_matrix(n)”](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-106-320.jpg)









![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 116
8. ESPACIOS VECTORIALES Y
APLICACIONES LINEALES.
8.1. DEPENDENCIA E INDEPENDENCIA LINEAL DE VECTORES.
COMBINACIÓN LINEAL.
EJEMPLO 8.1.
Estudiar si el vector v = (1,0,1,0) de R4 es combinación lineal de los vectores
u 1 = (0,1,2,−1), u 2 = (0,−1,1,0), u 3 = (0,1,0,1) .
Solución.
Este problema se puede resolver de varias formas. La manera clásica consiste en
plantear una ecuación vectorial del tipo
v = au 1 + bu 2 + cu 3
tal que si tiene solución, entonces el vector dado es combinación lineal de los restantes.
Para resolver este problema en DERIVE primero definimos los cuatro vectores
editando las expresiones:
“v:=[1,0,1,0]”, “u1:=[0,1,2,-1]”, “u2:=[0,-1,1,0]” y “u3:=[0,1,0,1]”.
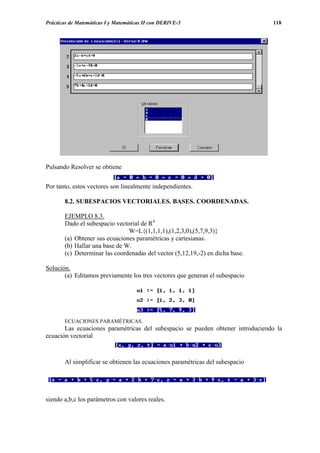
a continuación introducimos la ecuación vectorial
que al simplificar nos da
Obsérvese que la primera ecuación nunca se verifica lo cual nos indica que el sistema
carece de solución
Una segunda alternativa de resolución podría ser el estudiar el rango de la matriz
formada por los vectores. Si el rango es cuatro, esto quiere decir que son linealmente
independientes y, por tanto, no existe combinación lineal. Esto se puede comprobar
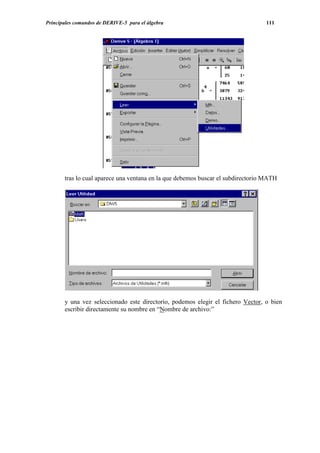
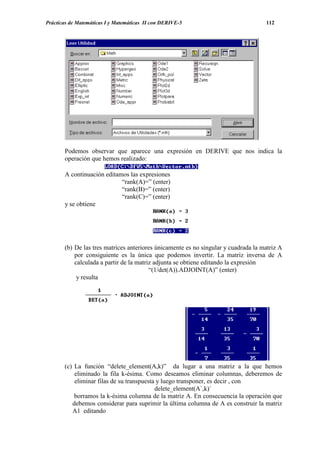
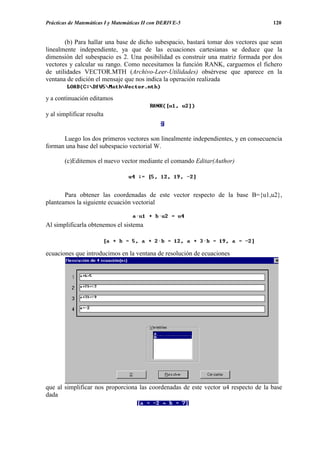
editando la expresión
que al pulsar (enter) nos da](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-118-320.jpg)










![Sistemas de ecuaciones lineales. 129
(b) Utilizando el comando SOLVE
(c) Utilizando el comando SOLUTIONS
(d) Utilizando la matriz inversa.
Veamos algunos ejemplos:
EJEMPLO 9.4.
Resolver el sistema del ejemplo 9.1 del apartado anterior, es decir:
2x+y-t-4u=4
3x-y+2z-5u=13
x+3y+z-t-6u=7
x+2y-3z-2t-2u=-7
Solución.
Como ya tenemos definido en DERIVE su matriz de coeficientes en la variable “a”
únicamente nos faltaría definir el vector de incógnitas editando
“inc:=[x,y,z,t,u]”
y el de términos independiente mediante
(a) Resolución por TRIANGULACIÓN DE GAUSS .
La función ROW_REDUCE calcula la matriz reducida de Gauss-Jordan. Esta
función admite dos formas o bien introducir como argumentos la matriz de coeficientes y
el vector columna de términos independientes, es decir editando “row_reduce(a,tin)=” y se
obtiene
o bien incluyendo como único argumento el de la matriz ampliada, que en este caso
tendríamos que volver a reeditar:](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-131-320.jpg)

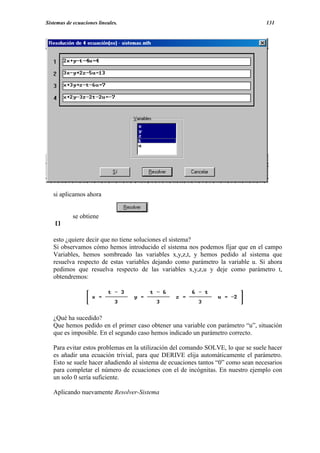
![Sistemas de ecuaciones lineales. 133
que es un sistema equivalente cuyas soluciones son:
x=-1+1/3 t, y=2+1/3 t , z=2+ 1/3 t, u=-2.
(C) Utilizando la función SOLVE:
Debido a la incomodidad que original tener que manejar esta secuencia Resolver-
Sistema, suele ser más cómodo aplicar la función SOLVE. Esta función tiene dos
argumentos, en el primer debemos indicar el vector de ecuaciones a resolver (editar las
ecuaciones entre corchetes) y en el segundo se indica el vector de incógnitas respecto de
las cuales queremos realizar la resolución. Así por ejemplo para resolver el sistema
anterior, podemos editar la expresión
“solve([ecuación 1, ecuación 2, ecuación 3, ecuación 4], [x,y,z,t]) “ si queremos
resolver respecto de las variables x,y,z,t y se obtiene
que al simplificar con resulta
es decir no hay soluciones, sin embargo si ahora reedito la expresión SOLVE tomando
ahora como variables de resolución [x,y,z,u] se obtiene
Si por el contrario lo que deseamos es obtener la resolución tomando todas las
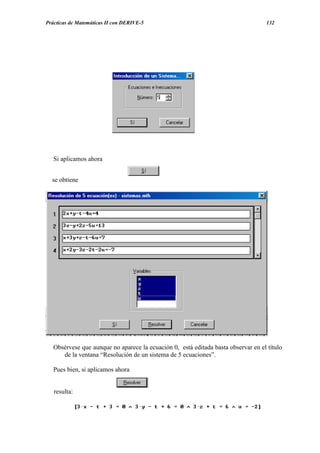
variables que aparecen, reeditanto la expresión
que al simplificar nos da
que es un sistema equivalente cuyas soluciones son:
x=-1+1/3 t, y=2+1/3 t , z=2+ 1/3 t, u=-2.
En realidad este es el COMANDO que se utiliza cuando se aplica Resolver-
Sistema. Esto se puede observar si
una vez editadas las ecuaciones](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-135-320.jpg)
![Prácticas de Matemáticas II con DERIVE-5 134
si ahora aplicamos el boton se obtiene
es decir la estructura de una instrucción que contiene el comando SOLVE.
(D) Utilizando la función SOLUTIONS:
Otra función que sirve para resolver sistemas en la función SOLUTIONS. Si en
vez de usar la función SOLVE , usamos la función SOLUTIONS tomando como
variables de resolución [x,y,z,u] se obtiene
que al simplificar
Obsérvese que la función SOLUTIONS genera una lista de puntos mientras que
cuando se usa la función SOLVE lo que se obtiene es una representación del punto
intersección que no puede ser ni dibujada ni usada para realizar operaciones tales como la
suma de vectores.
Si ahora lo que deseamos es obtener la resolución tomando todas las variables
que aparecen, reeditando la expresión](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-136-320.jpg)
![Sistemas de ecuaciones lineales. 135
que al simplificar nos da
que es el conjunto de soluciones parametrizado donde en este caso el parámetro es el
símbolo @1. Mientras que la función SOLVE nos da un sistema equivalente.
EJEMPLO 9.5.
Resolver el sistema de ecuaciones dado en el ejemplo 9.2 del apartado anterior, es
decir
2x - y - 2z = -2
-x +y+z = 0
x -2y + z = 8
2x - 2y = 6
Solución:
Si intentamos resolver utilizando el comando SOLVE, aprovechando que teníamos
definida en la variable “b” la matriz de coeficientes, el sistema se obtiene editando y
simplificando la expresión “b.[x,y,z]=[-2,0,8,6]”
utilizando este dato anterior podremos ahora editar la expresión
“solve(b.[x,y,z]=[-2,0,8,6],[x,y,z])”
que al simplificar nos da la solución del sistema planteado:
Como el número de ecuaciones es superior al de incógnitas, no es necesario añadir ninguna
ecuación trivial.
Si utilizamos la función ROW_REDUCE , como ya tenemos definida en la variable
“mb” la matriz ampliada, bastará editar y simplificar “row_reduce(mb)=” resultando](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-137-320.jpg)

![Sistemas de ecuaciones lineales. 137
es decir su rango es 2, luego SISTEMA COMPATIBLE INDETERMINADO.
Las soluciones en ese caso se pueden calcular mediante ROW_REDUCE; editando
“row_reduce(m(2))=”
por tanto x=-z, y=0.
También se podría resolver usando la función SOLUTIONS. Para lo cual debemos
editar la expresión “SOLUTIONS( m(2).[x,y,z]=[0,0,0], [x,y,z])”
que al simplificar nos da el conjunto de soluciones
EJERCICIO 50.
Discutir y resolver, cuando sea posible, los siguientes sistemas
x − 2y + z + t = 4 x + 2y − z + t + u = 0
2 x − y + z − 5t = −17 3x − y + t − u = 6
(a) (b)
3 x + 3 y − 10t = −31 6x + y + t + u = 1
4 x − 5 y + 3 z − 3t = −10
x − 2 y + 2 z − 2t = −5
EJERCICIO 51.
Estudiar según los valores del parámetro “a” el siguiente sistema y resuélvelo cuando sea
posible
2 x + ay + z = 4
ax + 2 y + z = 2
x + y + (a + 1) z = 3
EJERCICIO 52.
Discutir según los valores de “a” y “b” el siguiente sistema y resolverlo cuando sea posible
x+ y+z =3
2 x − ay + 3z = 4
3x − 3 y + 4 z = 7
5 x − (a + b) y + 7 z = 8 − b
](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-139-320.jpg)
![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 138
10. DIAGONALIZACIÓN.
10.1. PRINCIPALES FUNCIONES DE DERIVE PARA LA
DIAGONALIZACION: CALCULO DE AUTOVALORES Y
AUTOVECTORES.
Antes de iniciar el estudio de los principales conceptos que componen la
DIAGONALIZACIÓN de matrices, vamos a mostrar algunas funciones de DERIVE, útiles
en este contexto. Algunas de ellas están predefinidas y otras se contienen en el fichero de
utilidades VECTOR.MTH.
(A) Funciones predefinidas en DERIVE.
Sea A una matriz cuadrada:
DET(A) — calcula el determinante de la matriz A.
TRACE(A) — calcula la traza de la matriz cuadrada A.
CHARPOLY(A) — calcula el polinomio característico de la matriz A.
EIGENVALUES(A) — calcula los autovalores de la matriz A.
(B) Funciones del programa de utilidades VECTOR.MTH
RANK(A) — calcula el rango de la matriz A.
EXACT_EIGENVECTOR(A,v) — calcula los autovectores asociados al autovalor
v de la matriz A.
APPROX_EIGENVECTOR(A,v) — calcula los autovectores asociados al
autovalor v de la matriz A.
EJEMPLO 10.1.
1 −1 0
Dada la matriz A= − 1 2 − 1 calcular sus autovalores y el orden de multiplicidad
0 −1 1
de cada uno de ellos.
Solución
En primer lugar definimos en DERIVE la matriz dada editando con o bien con
Editar(Autor)-Expresion la expresión “a:=[[1,-1,0],[-1,2,-1],[0,-1,1]]” y se obtiene
A continuación calculamos sus autovectores directamente a través de la función
EIGENVALUES. Editando y simplificando la función
se obtiene
Otro método, consiste en calcular su polinomio característico mediante la función](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-140-320.jpg)






![Diagonalización. Autovalores y autovectores. 145
Se puede comprobar que efectivamente, se cumple la semejanza entre dichas
matrices.
EJEMPLO 10.4.
Estudiar para qué valores de los parámetros dados, es diagonalizable la siguiente
matriz:
Solución
Antes de editar la matriz, vamos a liberar de valores a los parámetros a y b
editando “a:=” y “b:=”
Ahora sí podemos editar la matriz “c” de forma usual “c(a, b):=[[a,b,0],[0,1,2],[0,0,2]]”
(obsérvese que editamos la matriz dependiente de los parámetros a y b, ya que esto nos
puede resultar muy útil a la hora de considerar unos parámetros determinados)
Sus autovalores se obtienen factorizando de forma racional su polinomio
característico, es decir editando y simplificando
De donde obtenemos que los autovalores de la matriz son w1=a, w2=1, w3=2.
A continuación pasamos a estudiar los distintos casos según los valores de “a”:
• Si a ≠ 1, a ≠ 2 entonces tendremos tres autovalores distintos, por lo que la matriz C
será diagonalizable.](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-147-320.jpg)



![Formas cuadráticas 149
11. FORMAS CUADRÁTICAS.
El objetivo de esta sección consiste básicamente en ofrecer una visión general de
cómo utilizar DERIVE para clasificar formas cuadráticas. Trataremos dos aspectos
fundamentales, por un lado la clasificación de una forma cuadrática dada por una matriz
simétrica de valores constantes utilizando los métodos de los menores principales y de los
autovalores, y en segundo lugar clasificar una forma cuadrática en función de los valores
de los parámetros que aparezcan en su matriz simétrica asociada.
11.1.OBTENCIÓN DE LA MATRIZ ASOCIADA A UNA FORMA
CUADRÁTICA.
EJEMPLO 11.1.
Encontrar la matriz simétrica asociada a las siguientes formas cuadráticas:
(a) q1(x,y,z,t) = -2x2+2xt-6yz+4z2+4tz+t2
(b) q2(x,y,z,t,u) = 3xy+xz+2xt+xu+3y2+7yz+8yt+5yu+2z2+5zt+8zu+t2+5tu+9u2
Solución.
Una posibilidad para obtener la matriz simétrica asociada a una forma cuadrática q
cualquiera consiste en considerar la matriz hessiana de q y dividir todos su elementos por
2, ya que la matriz hessiana de una forma cuadrática ha de ser simétrica pues toda función
polinómica cumple el Teorema de Schwartz.
DERIVE tiene predefinida una función que calcula el gradiente de una función
dada, indicando en el segundo argumento las variables de la función. Su sintaxis es
GRAD(función ó vector de funciones, variables)
Por tanto si calculamos el gradiente del gradiente obtendremos su matriz hessiana.
Entonces para definir en DERIVE una función que calcule la matriz simétrica asociada a
una forma cuadrática bastará con editar la expresión:
Estamos entonces en situación de resolver el ejemplo 1.
(a) Para introducir la forma cuadrática en DERIVE escribimos en Editar(Autor)-
Expresión
“q1(x,y,z,t):=-2x^2+2x t-6 y z + 4 z^2 + 4 t z + t^2”
y resulta
Si ahora editamos la expresión “s1:=matriz_simetrica(q1(x,y,z,t),[x,y,z,t])” y
simplificamos obtendremos la matriz simétrica de la forma cuadrática q1 guardada en la
variable S1.](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-151-320.jpg)
![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 150
(b) Escribimos en primer lugar la forma cuadrática mediante la expresión
“q2(x,y,z,t,u):=3x y + x z + 2 x t +x u + 3y^2+7y z + 8y t + 5y u + 2z^2+5z t
+ 8z u + t^2 +5t u + 9u^2”
resultando
A continuación editando y simplificando “s2:=matriz_simetrica(q2(x,y,z,t,u),[x,y,z,t,u])”
obtenemos
que es la matriz simétrica buscada.
Obsérvese que podríamos haber utilizado otro método, el que consiste en obtener
una matriz asociada cualquiera de la forma cuadrática y luego simetrizarla empleando la
regla conocida ½ (A+At).
11.2. CLASIFICACIÓN DE FORMAS CUADRÁTICAS CON MATRIZ
ASOCIADA DE VALORES CONSTANTES.
EJEMPLO 11.2.
Clasificar las formas cuadráticas definidas en el ejemplo anterior.
Solución.
(a) Vamos a utilizar en primer lugar el método de clasificación utilizando los
menores principales.](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-152-320.jpg)

![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 152
es decir, la forma cuadrática es indefinida.
Para utilizar el criterio de los autovalores, bastaría efectuar
Obsérvese que dado que DERIVE no consigue obtener los autovalores de forma directa,
veamos qué sucede si intentamos obtener el polinomio característico:
si intentamos resolver este polinomio obtenemos:
Pero incluso intentando resolver de forma numérica en el intervalo [-100,100] con
Resolver-Expresión:
obtenemos tan solo una raiz:
luego parece que en este caso el criterio de autovalores no podría aplicarse con el programa
DERIVE.
EJEMPLO 11.3.
Clasificar las siguientes formas cuadráticas:
−1 1 0 1 1 0
t t
(a) q 3 ( x) = x. 1 − 1 0 .x (b) q 4 ( x) = x. 1 2 0 .x
0 0 2 0 0 3
Solución:
(a) En primer lugar introducimos la matriz simétrica que define q 3 ( x) editando](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-154-320.jpg)
![Formas cuadráticas 153
Si intentamos clasificar la forma cuadrática utilizando el criterio de los menores
principales efectuando
observamos que este criterio no nos indica el tipo de q 3 ( x) , ya que el determinante es nulo.
Asi pues, aplicamos el criterio de los autovalores obteniendo
por lo que la forma cuadrática es indefinida.
(b) Editamos como habitualmente la matriz simétrica
Aplicando el criterio de los menores principales obtenemos
de donde, podemos deducir que la forma cuadrática es definida positiva.
11.3. CLASIFICACIÓN DE UNA FORMA CUADRÁTICA CUYA MATRIZ
DEPENDE DE PARAMETROS.
EJEMPLO 11.4.
Clasificar en función de los valores de “a” la forma cuadrática
q5(x,y,z)=ax2+4xy+y2+2xz+z2
Solución.
Definimos en primer lugar la forma cuadrática
La matriz simétrica asociada a dicha forma cuadrática se obtiene editando y simplificando
“matriz_simetrica(q5(x,y,z),[x,y,z])”
tras lo cual resulta](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-155-320.jpg)
![Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 154
Como la matriz tiene un parámetro, para facilitar cálculos posteriores, editamos la
expresión
“s5(a):=[[a,2,1],[2,1,0],[1,0,1]]”
obteniéndose
Procedemos a continuación a estudiar la matriz simétrica según los valores de a.
El determinante de la matriz es
Por tanto, podemos realizar una primera distinción de casos:
• Si a=5, entonces la matriz a clasificar es
Utilizando, por ejemplo, el criterio de autovalores, resulta
por tanto, para a=5 la forma cuadrática es semidefinida positiva.
• Si a≠5, estudiando los menores principales con
se tiene que:
- Si a>5, es claro que D3=det(S4)>0. En ese caso
D1=a>5>0 y
D2=a-4>0
Por tanto si a>5 es definida positiva.
- Si a<5, resulta que D3<0. Además como
D1=a, si 0<a<5 entonces D1>0 y D2=a-4<0 luego indefinida.
y si a<0, entonces D1<0 y D2<0 y también es indefinida.
Resumiendo:
a=5 semidefinida positiva
a>5 definida positiva
a<5 indefinida.
EJEMPLO 11.5.
Clasificar la forma cuadrática
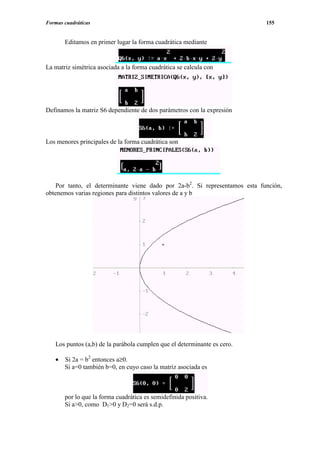
q6(x,y)=ax2+2bxy+2y2
según los valores de a y b.
Solución.](https://image.slidesharecdn.com/apuntesdeprcticasdederive-130417122012-phpapp02/85/Apuntes-de-practicas-de-DERIVE-156-320.jpg)