El documento detalla la función financiera de una empresa, que se centra en la captación y gestión de fondos para maximizar el valor de las acciones y el bienestar de los accionistas. Se analiza la estructura económica y financiera del balance, la importancia de la dirección financiera en la toma de decisiones de inversión y financiación, así como la relación entre estas estructuras. Además, aborda el equilibrio financiero, los objetivos financieros y el impacto de la función financiera en la salud económica de la empresa.

1. 1
Contenido
TEMA 1.- LA FUNCION FINANCIERA......................................................................................................................................2
1.1 INTRODUCCIÓN ..........................................................................................................................................................................................................2
1.2 OBJETIVOS DE LA FUNCION FINANCIERA DE LA EMPRESA.....................................................................................................................2
1.3 IMPORTANCIA DE LA DIRECCION FINANCIERA..............................................................................................................................................3
1.4 ESTRUCTURA ECONOMICA Y ESTRUCTURA FINANCIERA DE LA EMPRESA.....................................................................................4
1.4.1 Estructura Económica ........................................................................................................................................................................................4
1.4.2 Estructura Financiera..........................................................................................................................................................................................5
1.5 RELACIONES DE EQUILIBRIO ENTRE LAS ESTRUCTURAS ECONOMICAS Y FINANCIERAS.........................................................6
ANEXO TEMA 1..........................................................................................................................................................................7
CAPITALIZACIÓN Y ACTUALIZACION .........................................................................................................................................................................7
Capitalización..................................................................................................................................................................................................................7
Actualización .................................................................................................................................................................................................................10
RENTABILIDAD DE UNA INVERSIÓN.........................................................................................................................................................................14
COSTE DE LA FINANCIACIÓN .....................................................................................................................................................................................15
PROBLEMAS DE CAPITALIZACION Y ACTUALIZACION ....................................................................................................17

2. 2
TEMA 1.- LA FUNCION FINANCIERA
1.1 INTRODUCCIÓN
El subsistema financiero desarrolla una función clave dentro de la empresa. La empresa reacciona ante los
estímulos del mercado poniendo en marcha un sistema operativo capaz de producir y comercializar bienes o
servicios que permitan satisfacer las necesidades del mercado. La organización de su sistema operativo
supone la adquisición de activos reales. Muchos de ellos son activos tangibles como maquinaria, naves
industriales, etc. lo cual no sería posible sin la captación y generación de fondos. La demanda de bienes o
servicios por parte del mercado provoca, por tanto, una demanda derivada de fondos por parte de las
empresas, fondos que se recogerán en el pasivo de la empresa. Formando las dos partes fundamentales
del Balance que determinan el contenido de la función financiera.
Corresponde a la función financiera la captación de esos fondos a través de la venta de títulos o activos
financieros. Estos títulos tienen un valor ya que, incorporan derechos sobre los activos reales de la empresa. No
sólo son activos financieros las participaciones en el capital social, sino también las obligaciones, los préstamos
bancarios, etc.
El papel de la función financiera dentro de la empresa ha ido cambiando con el tiempo. El estudio de las
finanzas empresariales comenzó a principios de este siglo, y en una primera etapa abarcó hasta los años
cincuenta. Esta primera etapa denominada clásica o tradicional, se venía ocupando fundamentalmente del
estudio de las instituciones financieras y de los instrumentos financieros, pero siempre de una forma descriptiva.
A principios de la década de 1950, va apareciendo una nueva economía cada vez más competitiva, que reduce
los márgenes de rentabilidad de las inversiones, el mercado de capitales mejora su funcionamiento y se
desestabiliza el ambiente económico-financiero. A consecuencia de este nuevo contexto, el principal problema
con que se enfrentan los gerentes financieros no es ya la obtención de fondos sino el estudio de su mejor
utilización, es decir, el problema se ha trasladado del pasivo al activo del balance.
Como consecuencia de estos cambios en el medio socio-económico en que se desenvuelve la empresa,
aparece el nuevo enfoque de las finanzas con la aplicación en sus análisis de las modernas técnicas
cuantitativas.
Erza Salomon, que es uno de los más claros representantes de la aproximación analítica al estudio de las
finanzas, considera que la moderna administración financiera debe proporcionar los instrumentos analíticos
adecuados para dar respuesta a las tres siguientes cuestiones:
1.- ¿Cuáles son los activos específicos que debe adquirir una empresa?
2.- ¿Qué volumen total de activos debe tener una empresa?
3.- ¿Cómo financiar sus necesidades de capital?
Estas tres cuestiones están estrechamente ligadas. El volumen total de activo dependerá de las posibilidades
específicas de inversión, así como de las posibilidades de financiación. Las facilidades para obtener recursos
financieros dependerán a su vez de la cantidad y calidad de los proyectos de inversión en que van a ser
utilizados, puesto que los inversores estarán más dispuestos a aportar fondos para aquellos proyectos que sean
más prometedores y/o conlleven menos riesgo.
1.2 OBJETIVOS DE LA FUNCION FINANCIERA DE LA EMPRESA.
La función financiera es una de las funciones de la empresa, en consecuencia, debe con su objetivo contribuir
a reflejar el objetivo empresarial. Como toda organización, la empresa se compone de múltiples y variados
grupos (accionistas, directivos, trabajadores, clientes, proveedores, prestamistas, etc.) cada uno de los cuales
presenta fines y objetivos muy particulares y, en la mayoría de los casos no coincidentes, siendo los accionistas
el grupo prioritario o de mayor presión dentro de la empresa.
La función financiera debe fijar un objetivo que exprese los deseos de los accionistas, para ello necesitamos
cuantificar estos deseos, o bien establecer un índice de medida para los mismos. Clásicamente se tomaba

3. 3
como medida para este índice el beneficio, pretendiendo su maximización. La dificultad aparecía a la hora de
especificar el tipo de beneficio (a corto plazo, a largo plazo, antes o después de impuestos, si hablamos del
resultado total del ejercicio o del resultado para el accionista). Parece claro que debemos optar por maximizar el
beneficio después de impuestos que afecta exclusivamente al accionista, tal como podría ser el llamado
Beneficio por Acción, definido al dividir el beneficio neto de la empresa por el número de acciones ordinarias.
Si aceptamos el BPA como medida del beneficio para los accionistas, es claro que no estamos teniendo en
cuenta el momento en que se obtiene este BPA, ya que cualquier inversionista prefiere los beneficios presentes
a los futuros, y además, tampoco estaríamos considerando el riesgo asociado a estos beneficios, ni la política
de dividendos de la empresa, la cual representa para el accionista el pago líquido recibido cada año y, por tanto,
una variable fundamental a tener en cuenta.
En la actualidad, por las razones anteriores, se considera que la empresa debe conseguir el bienestar de sus
propietarios, entendiendo por bienestar la maximización de la riqueza y por propietarios a los accionistas. En
consecuencia, como la riqueza que poseen los accionistas, con respecto a la empresa, son las acciones, se
establece como objetivo financiero la maximización del valor de la empresa en el mercado para los
accionistas, es decir, la maximización del valor de las acciones (respetando los compromisos existentes entre
los distintos participantes en la organización). Admitiendo que el valor de éstas viene dado por la actualización
de los dividendos futuros a una tasa conveniente.
También podemos hablar de subobjetivos financieros subordinados siempre al objetivo general antes
mencionado, así, tendremos:
a) Crecimiento del beneficio.
b) Liquidez.
c) Rentabilidad financiera.
d) Maximización del margen sobre ventas.
e) Maximización del valor de la empresa.
f) Minimizar costes.
g) Etc.
1.3 IMPORTANCIA DE LA DIRECCION FINANCIERA.
El director financiero en función de su cargo:
- Participa en las decisiones de inversión en activos reales.
- Toma decisiones sobre las fuentes de financiación más convenientes en cada momento y su retribución, así
como la parte del beneficio que debe quedar en la sociedad en forma de reservas.
- Realiza la planificación de los recursos financieros tanto a largo como a corto plazo.
- Realiza la gestión financiera diaria que comprende aspectos tan diversos como: la tesorería, la gestión del
capital circulante, los impuestos, el proceso de datos, la contabilidad, etc.
La función financiera hoy es enormemente amplia y compleja, de forma que abarca todos los ámbitos de la
empresa. Toda decisión tomada puede repercutir, a corto o largo plazo, positiva o negativamente, en el devenir
de la vida empresarial, independientemente del ámbito donde se adopte, pues el más mínimo cambio en la
política de precios, en la expansión o restricción de la política de créditos, en la programación de inversiones,
etc. va a acabar repercutiendo en la cuenta de resultados.
Estas actividades de la función financiera, si la empresa es pequeña estarán realizadas por sus propietarios. Si
la empresa es grande, por una persona ajena a la propiedad de la empresa. Si la propiedad está muy repartida,
los administradores y directores disponen de libertad para la toma de decisiones, lo cual no ocurre en caso de
existir una alta concentración de la propiedad en manos de una persona o de un grupo reducido de personas.
Este hecho puede dar lugar a un conflicto de intereses entre tecnócratas y propietarios, de forma que puede
aceptarse para la función financiera los objetivos de los propietarios, siempre que sean compatibles con la
función de utilidad de la gerencia que es quien, en realidad, marca la prioridad entre los objetivos en una gran
empresa.
Las funciones básicas del director financiero se relacionan con las decisiones sobre las inversiones y con la
forma en que éstas son financiadas. Al realizar estas funciones, las responsabilidades del director financiero

4. 4
mantienen una relación directa con las decisiones fundamentales que afectan al valor de la empresa.
Decisiones que son:
- ¿Cuánto debe invertir la empresa y en qué activos concretos debe hacerlo?
- ¿Cuál debe ser la composición de los fondos necesarios para tales inversiones?.
El primer punto consiste en la toma de decisiones de inversión o presupuesto de capital de la empresa. La
dirección de la empresa debe decidir ante distintas alternativas que generan flujos de renta (beneficios) en
distintos períodos de tiempo y que comportan riesgos distintos (estrategias de diversificación, cambios en los
procesos productivos, etc.). La decisión de inversión se centra en la evaluación de los flujos financieros
(mediante una adecuada tasa de actualización), que previsiblemente generarán los proyectos de inversión.
El segundo punto consiste en la adquisición de fondos por parte de la empresa. La composición del pasivo
afecta al coste de capital, el cual determina el umbral de rentabilidad de las inversiones y la valoración de la
empresa. Dicha composición exigirá unas salidas de caja con motivo del pago de intereses, devolución del
principal y remuneración del capital propio.
La consecución de estas dos cuestiones se tiene que resolver teniendo en cuenta el objetivo de la empresa
que debe ser la maximización del valor de mercado de las acciones.
1.4 ESTRUCTURA ECONOMICA Y ESTRUCTURA FINANCIERA DE LA EMPRESA
Los activos que necesita la empresa así como, los pasivos y los recursos propios para financiarlos se
encuentran recogidos en el balance de la empresa. Balance que sigue siendo un modelo fundamental para el
análisis económico y financiero de la empresa. Cuando nos referimos al Balance en forma genérica, ha de
entenderse Balance de Situación, es decir aquél que representa el producto terminado del proceso contable de
un determinado período de tiempo.
El balance puede contemplarse desde un punto de vista jurídico, en cuyo caso representará, por un lado, los
bienes y derechos a favor de la empresa en un momento dado del tiempo (activo), por otro, las obligaciones
contraídas a esa fecha (pasivo) y, como diferencia el patrimonio neto perteneciente a los propietarios.
Desde una perspectiva económica, el balance muestra las fuentes de financiación existentes en un momento
dado, procedentes tanto de terceros ajenos a la empresa, como de los propietarios de la misma y la inversión o
aplicación que se ha dado a esa financiación.
1.4.1 Estructura Económica
La estructura económica se corresponde con el activo del balance, representa la inversión de la empresa,
también denominada capital de funcionamiento o capital productivo.
Las necesidades de capital productivo de la empresa vienen determinadas básicamente por la demanda
prevista y esperada para un período de tiempo más o menos largo del producto o productos que la empresa
elabora. En función de las tecnologías disponibles en el correspondiente sector de la actividad económica de la
empresa, se podrá determinar qué tipo de maquinaria va a utilizarse, qué tipo de naves industriales e
instalaciones se necesitan, elementos de transporte, inversiones financieras a largo plazo, etc. constituyendo la
parte fija de la estructura económica o activo.
Una vez determinada la inversión en activo fijo, se podrá determinar las inversiones en circulante que dependen
básicamente de la inversión en activo fijo y de la duración del ciclo de explotación (materias primas, productos
en curso, productos terminados. materiales auxiliares, etc.), procurando mantener un equilibrio entre sus
inversiones que le permita obtener una productividad alta.

5. 5
1.4.2 Estructura Financiera
Para financiar la adquisición de los elementos del capital productivo o de funcionamiento que aparecen
recogidos en el activo del balance, la empresa necesita disponer de recursos financieros o capital de
financiamiento.
En el pasivo y en el patrimonio neto del balance aparecen recogidos los diferentes tipos de recursos de que la
empresa ha hecho uso para la financiación del activo. A la empresa no le interesa utilizar un único tipo de
recursos financieros sino que, utiliza una mezcla o combinación de recursos financieros. Los diferentes tipos de
recursos financieros que la empresa puede utilizar pueden clasificarse en dos grandes grupos:
1.- Recursos financieros propios o financiación propia: Está formada por las aportaciones de los socios al
constituirse la sociedad y las sucesivas ampliaciones, en su caso. Se incluyen también dentro de esta rúbrica
las reservas o beneficios retenidos (autofinanciación por enriquecimiento) así como los fondos de amortización
y demás cuentas compensatorias del activo (autofinanciación por mantenimiento) cuando los correspondientes
fondos constituidos van a estar a disposición de la empresa durante un largo período de tiempo. En otro caso,
cuando la empresa va a necesitar disponer de dichos fondos en breve plazo, a los mismos habrá que incluirlos
dentro del pasivo exigible a corto plazo.
2.- Recursos financieros ajenos o financiación ajena: Está formada por las deudas o créditos de todo tipo.
Dentro de esta rúbrica procede distinguir a su vez dos grupos :
a) créditos a largo o medio plazo: son aquellos recursos que provienen de sujetos ajenos a la empresa y,
generalmente, está pactado mediante contrato previo la retribución y la forma de devolución.
b) créditos a corto plazo: fundamentalmente son de dos tipos, los créditos de provisión o créditos comerciales
que son los que la empresa obtiene como consecuencia de los aprovisionamientos (crédito de los proveedores,
de los suministradores de energía, del personal) y los créditos bancarios necesarios para paliar dificultades más
o menos transitorias de tesorería.
Las deudas o créditos de la empresa pueden ser también en forma de préstamos o de empréstitos: en los
préstamos existe un acreedor único o unos pocos acreedores, como ocurre con los créditos sindicados,
mientras que los empréstitos se hallan fraccionados en múltiples títulos de crédito, como ocurre con los
empréstitos de obligaciones, que se reparten entre múltiples acreedores.
Los recursos propios más los créditos a largo y medio plazo constituyen los denominamos capitales
permanentes de la empresa, porque están a disposición de la misma durante un largo período de tiempo, y el
capital social más las reservas por tiempo indefinido. Desde otra óptica, los recursos financieros pueden
clasificarse en internos o externos, según que sean generados en el interior de la empresa o sean captados por
la misma en el mercado financiero. El concepto de financiación interna es equivalente al de autofinanciación, en
su doble acepción de autofinanciación por mantenimiento y autofinanciación por enriquecimiento. El capital
social es la única fuente de financiación propia que es a su vez externa, porque afluye a la empresa desde el
mercado financiero.
La combinación entre recursos financieros propios y recursos financieros ajenos determinará la estructura
financiera de la empresa. A la hora de establecer las alternativas de financiación para la mejor estructura
financiera, debemos tener en cuenta:
a) El coste o precio de cada una de las alternativas financieras.
b) Las garantías que pueden ofrecerse.
c) Generalmente la financiación ajena es más barata puesto que las primas por riesgo serán menores para los
prestamistas que para los propietarios.
d) El coste de la financiación ajena es deducible del impuesto sobre beneficios, por lo que si i es el interés
nominal, el interés real será i(1-t), siendo t la tasa impositiva.

6. 6
1.5 RELACIONES DE EQUILIBRIO ENTRE LAS ESTRUCTURAS ECONOMICAS Y FINANCIERAS
Con carácter general, las diferentes masas del activo y pasivo han de mostrarse agrupadas con un criterio
homogéneo de liquidez, tanto activa como pasiva (grado de exigibilidad), lo que facilita su primera lectura. Así,
si el activo se clasifica de menor a mayor liquidez, el pasivo habría de agruparse de menor a mayor exigibilidad.
A continuación, se muestra de forma esquemática el balance ordenado según el criterio de menor a menor
liquidez:
ACTIVO NO
CORRIENTE
RECURSOS
PROPIOS
PASIVO NO
CORRIENTE
ACTIVO CORRIENTE
PASIVO
CORRIENTE
Esta presentación del balance nos permite comprobar la adecuación de la utilización de los recursos
financieros, ya que, existe un principio de equilibrio financiero que establece que:
- las inversiones e inmovilizaciones técnicas o financieras, es decir el activo fijo, así como la parte estable del
circulante han de ser financiadas con recursos a largo plazo o financiación básica.
- las inversiones circulantes de la empresa han de ser financiadas con recursos a corto plazo o pasivo
circulante.
De esta forma, una empresa está en equilibrio financiero cuando es capaz de hacer frente a todos sus
compromisos de pago, es decir, cuando es solvente.
La medida del equilibrio financiero es el fondo de maniobra o capital corriente. El fondo de maniobra se debe
estudiar desde dos vertientes: el fondo de maniobra real y el que debe ser (necesario).
La definición del fondo de maniobra real lo podemos obtener de la ecuación fundamental del balance:
AC + AF = PC + ELP + RP
y suponiendo una situación de equilibrio financiero normal, es decir: AC > PC ; ANC < PNC + RP, podemos
definir el capital corriente CC, atendiendo a su estructura como la parte del activo corriente que no se financia
con pasivo a corto sino con capitales permanentes.
CC = AC - PC
o bien, atendiendo a su financiación, como la parte de capitales permanentes que no financia activo no
corriente, sino que financia activo corriente:
FM = RP + PNC - ANC
Dada la importancia que el capital corriente tiene para la economía de la empresa, es conveniente que su
volumen sea el adecuado (necesario) en cada momento, dadas las características internas y externas de la
empresa.
La búsqueda del capital corriente que necesita una empresa para poder funcionar sin problemas en razón de
sus inversiones en inmovilizado, implica determinar al menos aproximadamente, el volumen mínimo de cada
uno de sus componentes.

7. 7
ANEXO TEMA 1
CAPITALIZACIÓN Y ACTUALIZACION
Capitalización
En la introducción se dice que las finanzas consisten en asignar recursos financieros (dinero) a través del
tiempo en distintas alternativas. Pero el dinero no vale lo mismo a través del tiempo, un euro hoy vale más
que un euro recibido dentro de un año. Si en vez de recibir un euro hoy lo recibo en el futuro, estoy dejando
pasar el beneficio potencial que obtendría con ese euro hoy. El beneficio potencial que dejo de disfrutar hoy
por esperarme a recibir ese euro en el futuro, se denomina “coste de oportunidad”. Este coste de
oportunidad es el valor temporal del dinero (interés).
Este concepto del valor temporal del dinero es el que debemos tener en cuenta en cualquier actividad
empresarial. Ya que nos permitirá medir el resultado de nuestras decisiones en el presente, calculando el
valor de los beneficios futuros de nuestra decisión al momento actual.
Para valorar la decisión de invertir hoy un capital, debemos conocer:
- Cómo obtener los resultados dependiendo del vencimiento de la inversión.
- Qué es más interesante, recibir al vencimiento los resultados, o bien recibirlos periódicamente.
- Qué me interesa más, recibir los resultados periódicamente o que estos se vayan acumulando al capital
inicial hasta su vencimiento.
Por ejemplo, disponemos de un capital de 12.000 € y queremos invertirlo durante dos años, tenemos dos
alternativas:
El Banco A nos ofrece un interés del 6% anual, a pagar al vencimiento.
El Banco B nos ofrece un interés del 5.90% anual, pero los intereses los calcula trimestralmente.
¿En qué Banco realizamos la inversión?
Para tomar esta decisión necesitamos conocer el concepto de capitalización, que nos explica como
aumenta el dinero a lo largo del tiempo cuando se invierte.
La capitalización tiene por objeto calcular el valor de un capital en un momento cualquiera del tiempo Cn
(que recibe el nombre de montante o capital final), conocido el valor de ese capital en otro momento anterior
C0 (que recibe el nombre de capital inicial).
La operación de capitalización supone que el capital inicial va a devengar o producir intereses desde el
momento inicial hasta el momento final. Estos intereses se irán devengando por periodos de tiempo
determinados (meses, semestres, años, etc.), a partir de los cuales se acumularán o no al capital inicial para
producir nuevos intereses en los periodos sucesivos.
Si los intereses no se acumulan al capital inicial, nos encontramos con la capitalización simple, y si los
intereses se acumulan al capital inicial, nos encontramos con la llamada capitalización compuesta.
Capitalización simple
Para explicar la capitalización simple, podemos utilizar el siguiente ejemplo: Supongamos un capital inicial
de 1 €. Los intereses anuales vienen expresados en tanto por ciento: 3% quiere decir que por cada 100 €
que preste durante un año, obtendré 3 €. Pero el tipo de interés anual también se puede plantear en tanto
por uno, es decir, por cada euro prestado recibiré 0,03 €. De esta forma transcurrido un año recibiré:
(1+0,03) = 1,03 € por cada euro prestado.
Si presto 1.000 € durante un año al 3% recibiré al final del año: 1.000 x (1 + 0,03) = 1.030 €. Esta cantidad
la podemos expresar también como: 1.000 + 1.000 x 0,03 = 1.000 + 30 = 1.030. Donde los 1.000 €
representan la devolución del capital inicial y los 30 € los intereses.

8. 8
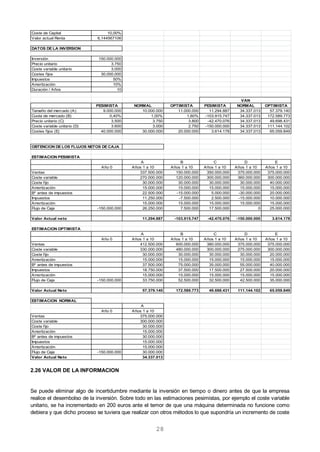
Cuando hablamos de la capitalización simple debemos tener en cuenta que los intereses anuales siempre
se calculan sobre el capital inicial. Así, si los 1.000 € los prestamos durante dos años, al final del periodo,
obtendremos: 1.000 + 1.000 • 0,03 + 1.000 • 0,03 = 1.000 + 30 + 30 = 1.060 €.
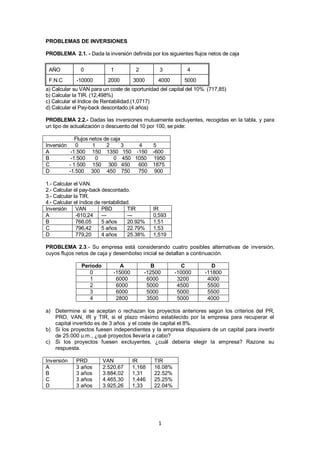
De esta forma, obtendremos el capital al final de cualquier periodo expresado en años. Las fórmulas a
utilizar son las relacionadas en la siguiente tabla:
Periodo Capital inicial Intereses Capital final
1
2
...
n
C0
C0(1+i)
...
C0[1+(n-1)i]
C0i
C0i
...
C0i
C1= C0 + C0i = C0 (1+i)
C2 = C0(1+i) + C0i = C0(1+2i)
.....
Cn= C0(1+ni)
Si cambiamos el periodo de capitalización anual por periodos inferiores al año para el cálculo de los
intereses, tendremos en cuenta que, si un euro capitalizado durante un año produce 0,03 €, cuando lo
prestamos por un semestre (medio año), producirá: 0,03/2 = 0,015 €, más el euro aportado inicialmente, es
decir, 1 + 0,015 = 1,015.
En la capitalización simple los intereses son proporcionales al tiempo. Si prestamos 1.000 € durante 80 días,
al final de dicho periodo tendremos: 1.000 + 1.000 • (0,03/365) x 80 = 1.000 + 6,57 = 1.006,57 €.
Como el tanto unitario es por año, 0,03 € por cada euro prestado a un año, cuando el periodo de
capitalización sea inferior al año, podemos expresar dicho periodo como una fracción de año: prestar 1.000
€ durante 80 días es lo mismo que prestarlos durante 0,219 de año (80/365). De esta forma obtendríamos al
final de los 80 días: 1.000 + 1.000 x (80/365) x 0,03 = 1.000 + 1000 x 0,219 x 0,03 = 1.006,57 €.
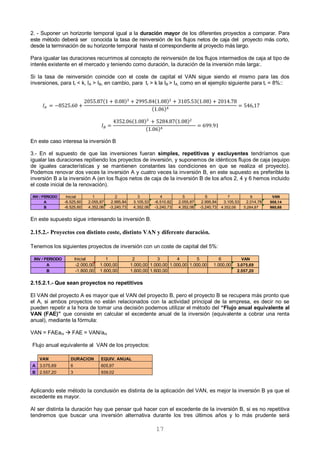
El término: 1.000 x (80/365) • 80 corresponde a los intereses producidos durante el periodo de 80 días, lo
que también podemos expresar como:
Expresión que nos permite cuantificar el importe de los intereses producidos en la capitalización simple para
periodos de capitalización expresados en días.
Cuando los periodos son otros, por ejemplo, meses o años, tendríamos:
Capitalización compuesta
En la capitalización compuesta, los intereses producidos al final de cada periodo se acumulan al capital
existente al inicio del periodo, de esta forma, mientras dure la operación de capitalización, los intereses
producidos en cada periodo van a su vez a producir más intereses.
Ejemplo: Colocamos en una entidad financiera un capital de 1.000 € al 5% anual, durante tres años, la
evolución de la operación financiera es la siguiente:
Año 0: 1.000
Año 1: 1.000 + 0.05x1.000 = 1.000 + 50 = 1.050
Año 2: 1.050 + 0.05x1.050 = 1.050 + 52,5 = 1.102,5
Año 3: 1.102,5 + 0.05x1.102,5 = 1.102,5 + 55,12 = 1.157,62
36500
57,6
500.36
380000.1
100
3
365
80
000.1
0tiC
I
xx
xx


100
ti0C
I:añospara
1.200
ti0C
I:mesespara



9. 9
Año 0: Co
Año 1: C1 = Co + Coi = Co(1+i)
Año 2: C2 = C1+ C1i = C1(1+i) = Co(1+i)(1+i) = Co(1+i)2
= C2
Año 3: C3 = C2 + C2i = C2 (1+i) = Co(1+i)
2
(1+i) = Co(1+i)
3
...........................
fórmula general: Cn = Co(1+i)n
la expresión: (1+i)
n
se le llama factor de capitalización.
Cuando la capitalización es por periodos de tiempo inferiores al año lo primero que tenemos que hacer es
calcular el porcentaje correspondiente al periodo que será igual al tanto anual (también llamado ‘tanto
nominal’) dividido por el número de periodos que hay en el año.
Por ejemplo, si el tanto que nos dan es el 6% anual pero capitalizado por semestres, el porcentaje del
semestre será el resultado de dividir: 0,06/2 = 0,03, siendo 0,03 el tanto efectivo del semestre. Un depósito
de 1.000 € a un año al 6% capitalizado por semestre obtendríamos el siguiente resultado al final del año:
Año 0 = 1.000
1º semestre: 1.000 + 1.000x0,03 = 1.030
2º semestre: 1.030 + 1.030x0,03 = 1.060,9
El resultado final es de 1.060,9 €, como vemos, es superior al 6% nominal anual ofrecido. Esto se debe a
que los intereses producidos en el primer semestre producen a su vez intereses durante el segundo
semestre.
Este resultado es equivalente a realizar un depósito de 1.000 € al 6,09% capitalizado anualmente. En este
caso se dice que el 6,09% es un tanto anual equivalente (TAE) al 6% nominal anual pero capitalizado por
semestres. La fórmula para obtener el TAE en este ejemplo es:
la fórmula general:
donde:
int. anual = interés nominal anual ofrecido.
m = número de periodos del año (número de veces durante el año en el que se van a producir intereses).
Ejemplo 1.- Está pensando en invertir 1.000.0000 € a un año. Ha preguntado en tres bancos distintos y le
han ofrecido las siguientes condiciones:
Banco A: 15% anual con abono diario de intereses.
Banco B: 15.5% anual con abono de intereses trimestrales.
Banco C: 16% anual con pago de intereses al final del año.
¿Qué Banco le ofrece mejores condiciones?
Banco A  0,15/365 = 0,0004109  1.000.000(1,0004109)365
= 1.161.798
TAE: 16,1798%
Banco B  0,155/4 = 0.03875  1.000.000(1,03875)4
= 1.164.244
TAE: 16,42%
Banco C  0,16  1.000.000(1,16) = 1.160.000
TAE: 16%
Solución: Banco B
 TAE





 1
2
06.0
1
2
 TAE1
m
m
anualint.
1  






10. 10
Ejemplo 2.- Colocamos un depósito de 30.000 € en una entidad financiera que abona un interés nominal del
6% anual durante cinco años. ¿Cuál sería el capital final transcurridos esos cinco años?
Supongamos que los intereses se abonan por trimestres. ¿Cuál sería el capital final transcurridos los cinco
años?
Ejemplo 3 .- Suponga que tiene en la actualidad una participación en un fondo de inversión valorada en
7.000 €. El director del banco le garantiza una rentabilidad a su fondo de inversión del 8% anual, si aporta
a dicho fondo de inversión 4.000 € cada año, durante los próximos tres años. ¿Cuál será el valor del fondo
de inversión al final de los tres años?.
Tenemos que capitalizar las aportaciones realizadas hasta finalizar el plazo de la operación.
La aportación actual permanece invertida en el fondo durante tres años: 7.000(1+0.08)
3
= 8.817,98
La aportación al final de primer año permanece invertida en el fondo durante dos años: 4.000(1+0.08)2
=
4.665,6
La aportación al final de segundo año permanece invertida en el fondo durante un año: 4.000(1+0.08) =
4.320
Al finalizar el tercer año tendremos: 8.817.98 + 4.665.6 + 4.320 + 4.000 = 21.803,58
Actualización
En la capitalización hemos estudiado a partir de un capital inicial, como aumenta el capital a lo largo de un
número determinado de años, cuando se invierte a un tipo de interés. En este apartado el planteamiento es
justo el contrario: ¿qué vale hoy un capital que vamos a recibir dentro de unos años? ¿En qué decisiones
me va a ayudar la actualización?
- Suponga que ha recibido unos títulos del Estado que vencen en el año 2.010 por un importe de 10.000
€. Si hoy tiene la necesidad de vender esos títulos, ¿por cuánto podría venderlos?.
- Está interesado en comprar una vivienda dentro de tres años. Su precio será de 200.000 €. ¿Qué
cantidad de dinero tendría que depositar hoy en un banco dado un determinado tipo de interés, para
conseguir los 200.000 € dentro de tres años?
- En obtener la rentabilidad de sus inversiones: Un banco le ofrece la posibilidad de participar en un fondo
de inversión aportando hoy un determinado capital que se va a recuperar junto con sus intereses
durante los próximos años, ¿qué rentabilidad obtengo del fondo de inversión?
Se define la actualización como: La operación de hallar el valor de un capital en un momento del tiempo,
conocido el valor de ese capital en un momento posterior. También se conoce como descuento. Es la
operación inversa a la capitalización.
Tenemos dos tipos de actualización o descuento:
• Actualización simple.
• Actualización compuesta.
Actualización simple
Consiste en calcular el valor actual de un capital a cobrar a corto plazo (para períodos inferiores al año).
Ejemplo 4.- Supongamos que vamos a cobrar 1.000 € dentro de un año, el interés anual está al 5%. Si
necesito anticipar a hoy ese cobro futuro, ¿cuánto recibiría?
77,146.40)06.01(30000 5
5 C
65,405.40
4
06.0
130000
5*4
5 





C

11. 11
Para calcular el valor actual partimos de la expresión de la capitalización:
a la expresión:
)1(
1
i
se le llama factor de actualización.
A la diferencia entre lo que tenía que recibir y lo que recibo, se le llama descuento:
Recibir hoy 952,38 € es equivalente a recibir 1.000 € dentro de un año.
Se dice que dos capitales son equivalentes cuando sus valores actuales son iguales: 1.000 € de dentro
de un año, hoy valen 952,38 €, por tanto, es indiferente cobrar hoy esa cantidad o esperarse un año y
cobrar los 1.000 €.
Si quisiera hacer un depósito a un año con el importe cobrado siendo el interés anual del 5%, el resultado
sería:
C1 = 952,38(1+0,05) = 1.000
Pero, en la práctica, el tipo de descuento simple que se aplica es el llamado comercial, que consiste en
calcular el descuento D en lugar de, por la diferencia entre el capital final y el inicial, mediante la fórmula:
En este caso, ambos capitales ya no son equivalentes. No da lo mismo recibir hoy 950 € que 1.000 € dentro
de un año. Esto lo comprobamos cuando queremos reinvertir el capital obtenido en el descuento al 5% a un
año:
C1 = 950 x (1,05) = 997,5 < 1.000
Si queremos anticipar el cobro de 1.000 € de dentro de 91 días a hoy, sabiendo que los intereses están al
5% anual, lo primero sería aplicar la fórmula del descuento:
En el denominador dependiendo del periodo de actualización pondremos: 100 cuando sea anual; 36.500 o
36.000 cuando sean días (según consideremos el año civil o si consideramos el año comercial); 1.200
cuando sean meses.
   i1
1
1
C
i1
1C
0Cdespejandoi)(10C1C




)1()1(
11
101
i
iC
i
C
CCCD




47.62952,381.000Dsiendo
952,38
0.051
1.000
0C




950501.000D1C0Csiendo
50,
100
1000x1x5
100
ti1C
D










100
i
x
360
t
11C
36.000
it1C
1C0C
:símbolosmedianteexpresamoslosi
987,3612,641.0000C:por tanto12,64;
36.000
1.000x5x91
D

12. 12
Actualización compuesta
Consiste en calcular el valor actual de un capital a cobrar a largo plazo (para períodos superiores al año).
Ejemplo 5.- Supongamos que vamos a cobrar 1.000 € dentro de dos años, el interés anual está al 5%. Si
necesito anticipar a hoy ese cobro futuro, ¿cuánto recibiría?
Para calcular el valor actual partimos de la expresión de la capitalización:
Si suponemos ahora que tenemos que cobrar dos capitales de 1.000 € dentro de un año y 1.000 € dentro de
dos años. ¿Hoy que valen?:
VA(1.000) = 1.000/(1.05) = 952.38
VA(1.000) = 1.000/(1.05)2
= 907.37
Al estar referidos los dos capitales al momento actual, podemos sumar sus valores actuales: 952.38 +
907.37 = 1.859,41
En vez de calcular los valores actuales paso a paso, podemos utilizar la siguiente expresión:
Como ya hemos dicho anteriormente, los 1.859,41 € de hoy son equivalentes a 1.000 € de dentro de un año
y a 1.000 € de dentro de 2 años.
Teniendo en cuenta que varios capitales son equivalentes cuando sus valores actuales son iguales,
podemos utilizar esta definición para poder mover en el tiempo distintos capitales.
Supongamos que hoy quiero efectuar un depósito en € en el banco que me permita disponer de 1.000 €
dentro de un año y de otros 1.000 € dentro de dos años, siendo los intereses del 5% ¿de qué importe debe
ser el depósito?
Para ello, tendré que calcular qué capital hoy (C0 ) es equivalente a recibir 1.000 dentro de un año y 1.000
dentro de dos años. Utilizando la definición de capitales equivalentes:
C0 = VAC1 + VAC2 = VA(1.000) + VA(1.000) = 952,35 + 907,03 = 1.859,41 es el importe del depósito que
ingresaré hoy en el banco.
Demostración:
Capital al finalizar el año 1: 1.859,41x(1,05) – 1.000 (que retiramos al finalizar el primer año) = 952,38
Capital al finalizar el año 2: 952,38x(1,05)(*) – 1.000 = 0
(*) se multiplica por 1,05 ya que lo capitalizamos un año desde fin año 1 hasta fin año 2.
Ejemplo 6.-Dentro de 4 años una persona quiere sustituir su coche comprando otro nuevo al contado cuyo
coste será de 25.000 €. ¿Qué cantidad debe invertir hoy al 12% para poder hacer frente a dicho pago dentro
de 4 años?.
A partir de la expresión de la capitalización: CF = C0(1+i)n
donde:
CF = capital al final de “n” años.
C0 = capital inicial
n = número de años.
i = interés anual
   
03,907
205,01
1000
2i1
1C
0Cdespejando2i)(10C1C 




   2
i1
2C
i1
1C
VA




   
41,859.103,90738,952
05,1
1000
05,1
1000
20 C

13. 13
Sustituyendo los datos del ejemplo en la expresión anterior tenemos: 25.000 = C0 (1.12)4
Como se pide el “capital que debe invertir hoy”: C0, despejamos de dicha expresión C0 :
C0 = 25.000/(1.12)
4
= 15.887,95
¿Qué cantidad debe invertir al 12% para hacer frente a dicho desembolso si los intereses se van
produciendo trimestralmente? Si los intereses se van produciendo trimestralmente, quiere decir que el
interés que corresponde a cada trimestre es:
Por cada euro depositado en el banco al principio de cada trimestre obtendremos: 1+0.03 = 1.03 € al
finalizar el trimestre, el 3% es el tanto efectivo correspondiente a dicho período. Cuando finalice el primer
trimestre: 1 € se ha convertido en 1.03 €.
Al principio del segundo trimestre tenemos 1.03 € que finalizado el mismo se han convertido en:
1.03 x (1+0.03) = 1,03 x 1.03 = 1,0609
multiplicamos la cantidad de euros al principio del trimestre por lo que produce un euro durante el trimestre.
Al principio del tercer trimestre disponemos de 1,0609 € que finalizado el mismo se han convertido en: 1.032
x (1+0.03) = 1.032 x 1.03 = 1.0927
Multiplicamos la cantidad de euros al principio del trimestre por lo que produce un euro durante el trimestre.
De esta forma, transcurridos tres trimestres, 1 € depositado en el momento inicial, se ha transformado en:
1,0927 €.
Si queremos conocer en cuánto se ha transformado un euro dentro de 4 años si los intereses se van
produciendo trimestralmente, haremos lo siguiente: Número de períodos de capitalización: 4 años x 4
trimestres = 16 trimestres.
Un euro depositado en el momento inicial, su valor al final de los 16 trimestres será: (1.03)
16
= 1.6047 €
Como el ejemplo nos pide “el capital que debe invertir hoy” C0, para obtener 25.000 euros dentro de 16
trimestres, utilizando la fórmula de la capitalización compuesta, obtenemos:
Ejemplo 7.- Sabiendo que los intereses que paga un banco son del 11% anual: ¿Qué cantidad debe
ingresar hoy (C0) en el banco para que le abone 5.000.000 € dentro de cuatro, cinco y seis años?.
0 1 2 3 4 5 6
C0 5000000 5000000 5000000
Para resolver este apartado del Ejemplo, tenemos que recordar el concepto de capitales equivalentes que,
aplicados al Ejemplo sería: “tres capitales a recibir dentro de 4, 5 y 6 años son equivalentes a otro capital a
recibir en el momento actual, cuando sus valores actuales son iguales”.
VA4(5.000.000) = 5.000.000/(1.11)
4
= 3.293.654,9 + VA5(5.000.000) = 5.000.000/(1.11)
5
= 2.967.256,6 +
VA6(5.0000000) = 5.000.000/(1.11)
6
= 2.673.204,2 = 8.934.115,7
03.0
4
12.0

n
4
i
10CnC 






 
15.579,17
16
1.03
25000
0C
16
4
0.12
10C25.000 







14. 14
Si no retiramos del banco ninguna cantidad hasta el sexto año ¿Cuál será el valor al final del año sexto de
las tres cantidades?
En este apartado nos piden el valor futuro de un capital, es por tanto, una operación de capitalización, el
período de capitalización será desde el momento en que se recibe hasta el vencimiento:
VF4 = 5.000.000(1.11)2
= 6.160.500
VF5 = 5.000.000(1.11) = 5.550.000
VF6 = 5.000.000
Total = 16.710.500
También lo podríamos haber hecho capitalizando el valor actual obtenido en el primer apartado del ejercicio,
hasta el año 6:
VA = 8.934.116(1,11)
6
= 16.710.500
Ejemplo 8.- Sabiendo que el interés que paga un banco es el 9% anual, ¿qué cantidad debe ingresar hoy en
el banco para que le permita disponer de 1.000.000 dentro de un año y de 2.000.000 de € dentro de dos
años?
Si el banco está pagando el 9% anual, tenemos que calcular hoy que vale 1.000.000 € a cobrar dentro de
un año y 2.000.000 € a cobrar dentro de dos años:
¿Qué vale hoy 1.000.000?  1.000.000/(1,09) = 917.431
¿Qué vale hoy 2.000.000?  2.000.000/(1,09)
2
= 1.683.360
Habrá que ingresar la suma de las dos cantidades: 2.600.791
Una vez comprendido el concepto de capitales equivalentes que nos permite desplazar capitales a través
del tiempo, podremos utilizar este método para definir conceptos como:
- rentabilidad de una inversión
- coste de una financiación
RENTABILIDAD DE UNA INVERSIÓN
Cuando una empresa realiza una inversión, espera recibir unos ingresos durante un número determinado de
años. La empresa necesita conocer el valor actual de esos ingresos a fin de determinar si es rentable o no
la inversión.
Suponga que le ofrecen participar en una inversión que le garantiza cobrar 5.000 € dentro de un año
aportando hoy 4.500 €, y quiere saber con esta información cuál sería la rentabilidad obtenida en esta
inversión. Si está de acuerdo en desprenderse hoy de 4.500 € para recibir 5.000 € dentro de un año, quiere
decir que, para usted ambos capitales son equivalentes, por tanto sus valores actuales son iguales:
r representa la tasa de actualización que iguala el valor actual de 5.000 € a recibir dentro de un año con el
importe de la inversión. A esa tasa de actualización, la denominamos rentabilidad. Despejando, obtenemos
r:
Cuando los capitales son equivalentes, el resultado de la inversión es cero:
Esta fórmula nos permite resolver otras cuestiones que se plantean en una inversión.
 r1
5.000
VA(5.000)4.500


11.11%0,111x100
4.500
4.5005.000
r 


 0,11111
5.000
-4.5000
0,11111
5.000
4.500





15. 15
Suponga que usted exige a sus inversiones una rentabilidad del 15%. En este caso, como la rentabilidad
obtenida es del 11,11% no invertiría.
También podría preguntarse cuánto tendría que invertir para conseguir esa rentabilidad del 15%. Lo que
podríamos expresar igualmente como ¿cuánto estaría dispuesto a pagar hoy por un activo que tiene un
precio de 5.000 € dentro de un año?
El precio de ese activo sería de 4.347,83 €.
Usted sigue exigiendo un 15% de rentabilidad a sus inversiones, pero le piden 4.300 € por participar
(comprar el activo), en este caso, ¿qué resultado obtendría?:
Obtendría un beneficio de 47,83 €. Es decir, estaría comprando un activo cuyo valor es superior a su precio.
A esta diferencia entre el valor actual de lo que recibe y el coste de la inversión lo llamamos valor actual
neto (VAN).
Ejemplo 9.- Suponga que le ofrecen comprar un activo que le va a generar los siguientes flujos monetarios:
Momento actual: pagar 150.000 €
Dentro de un año: pagar 100.000 €
Dentro de dos años: se vende por 300.000 €
¿Qué rentabilidad obtendría por la compra del activo? Para determinar la rentabilidad de un activo, debemos
igualar el valor actual de los pagos con el valor actual de los ingresos, siendo la tasa de actualización que
iguala unos flujos monetarios con otros, la rentabilidad de la inversión:
Ejemplo 10.- Queremos comprar un activo que ofrece los siguientes ingresos:
Desde el año 1 hasta el año 5: cobramos 100 € cada año
El año 6: cobramos 1.200 €.
Si nos piden comprar el activo por 1.100 €, ¿qué rentabilidad estamos obteniendo?
Si la rentabilidad que exige a sus activos es del 8%, ¿cuánto pagaría por el activo?
COSTE DE LA FINANCIACIÓN
Las empresas necesitan conseguir financiación para desarrollar sus planes de inversión. En el mercado
existen una gran variedad de instrumentos de financiación (acciones, obligaciones, préstamos, cuentas de
crédito, etc.). Toda financiación representa para la empresa una entrada de dinero que, tendrá que devolver
durante los próximos años.
 
83,347.4
15.01
5000
0 

C
 
83,47
15.01
5000
43000 


   
%963,1111963.0
1
000.300
1
000.100
000.150 2




 r
rr
           
%091,9
1
1200
1
100
1
100
1
100
1
100
1
100
100.1 65432













rrrrrr
           
1.155,47
6
1.08
1200
5
1.08
100
4
1.08
100
3
1.08
100
2
1.08
100
1.08
100
P 

16. 16
Tendremos que obtener el valor actual de todos los pagos que ocasiona la financiación para poder
compararlo con la cantidad recibida, para conocer el coste de la financiación.
Suponga que le prestan hoy 4.500 € teniendo que devolver 5.000 € dentro de un año y quiere saber con
esta información, ¿cuál sería el coste financiero del préstamo? Para ello, recurrimos al concepto de
capitales equivalentes. Si está de acuerdo en recibir hoy 4.500 € para pagar 5.000 € dentro de un año,
quiere decir que, para usted ambos capitales son equivalentes, por tanto sus valores actuales son iguales:
 i
VA


1
000.5
)000.5(500.4
i representa la tasa de actualización que igual el valor actual de 5.000 de dentro de un año con el importe
del préstamo. A esa tasa de actualización, la denominamos coste de la financiación y, despejando,
obtenemos i:
Si queremos obtener el coste de la financiación cuando la devolución del préstamo la realizamos en varios
años, debemos igual el importe del préstamo con el valor actual de todos los pagos previstos.
Ejemplo 1.- Supongamos que pedimos un préstamo de 30.000 € para devolver en cinco años a razón de
7.500 € al año, y queremos saber cuál es el coste de dicho préstamo.
El planteamiento consiste en igualar el valor actual del préstamo con el valor actual de los pagos:
Resolviendo la ecuación obtendríamos el coste del préstamo. Para resolver esta ecuación necesitamos
tener una hoja de cálculo. También podemos utilizar un método aproximado que consiste en sustituir los
pagos futuros por un único pago igual a la suma de todos ellos y, tomando como vencimiento de ese único
pago el vencimiento medio de todos los pagos. La fórmula quedaría:
a este método se le llama “método aproximado del vencimiento medio”.
%11.11100*111,0
4500
45005000


i
         5432
1
7500
1
7500
1
7500
1
7500
1
7500
000.30
iiiii 









1
*
/1
0
=i 


 















t
Pagos
t
t
Pagos
P
t
Pagos
%72,70772.01
30000
75007500750075007500
75007500750075007500
5*75004*75003*75002*75001*7500
1





 
 







i

17. 17
PROBLEMAS DE CAPITALIZACION Y ACTUALIZACION
PROBLEMA 1 - Hallar el valor actual de una cantidad que colocada al 12% de interés compuesto, producirá
10.000.000 de euros dentro de 10 años. (Sol: 3.219.732 euros)
PROBLEMA 2. - En la actualidad tiene 7.000.000 de euros en una cuenta bancaria que le paga un 8% de
interés anual. Está pensando en ingresar 4.000.000 de euros al final de cada uno de los próximos tres años.
¿Cuánto tendrá en tres años?. ¿Cuánto tendrá en cuatro años?. (Sol: 21.803584 euros 23.547.871 euros)
PROBLEMA 3. - Sabiendo que los intereses que paga un banco son del 9% anual, ¿qué cantidad debe
ingresar hoy en el banco para que le permita disponer de 1.000.000 dentro de un año y de 2.000.000 de euros
dentro de dos años?. (Sol: 2.600.791 euros)
PROBLEMA 4. - Sabiendo que los intereses que paga un banco son del 11% anual, ¿qué cantidad debe
ingresar hoy en el banco para que le abone tres pagos de 5.000.000 dentro de cuatro, cinco y seis años?.
¿Cuál será el valor al final del año sexto de los tres pagos?. (Sol: 8.934.116 euros; 16.710.500 euros)
PROBLEMA 5. - Esta pensando en invertir 1.000.0000 euros a un año. Ha preguntado en tres bancos distintos
y le han ofrecido las siguientes condiciones:
Banco A: 15 % anual con abono diario de intereses; Banco B: 15.5% anual con abono de intereses trimestrales;
Banco C: 16% anual con pago de intereses al final del año. ¿Qué Banco le ofrece mejores condiciones?. (Sol:
Banco B)
PROBLEMA 6. - Dentro de 4 años una persona quiere sustituir su coche comprando otro nuevo al contado
cuyo coste será de 25.000 euros ¿Qué cantidad debe invertir al 12% para hacer frente a dicho desembolso?.
(Sol: 15.887,95 euros).
PROBLEMA 7. - Un especulador recibe un ofrecimiento para comprar un terreno por el que pagarán 1 mill. de
euros dentro de 2 años. El rendimiento mínimo que exige a sus inversiones es del 10%. ¿Cuál es la cantidad
máxima que puede pagar hoy?. (Sol. 826.446,28 euros)
PROBLEMA 8. - Se tienen que hacer unos pagos fijos anuales de 1.200.000 euros durante los 6 próximos
años. Si el interés es del 8% ¿cuánto deberá tener hoy para hacer frente a esos pagos? (Sol: 5.547.455,59
euros)
PROBLEMA 9. - Ha pedido un préstamo de 1.000 euros y tiene que pagar 1.762 dentro de cinco años. ¿Cuál
es el tipo de interés con capitalización anual?. (Sol: 11,99 %)
PROBLEMA 10. - Determinar el tanto anual efectivo de un capital impuesto en un Banco que abona intereses
trimestralmente al tipo del 1,5% trimestral. (Sol: 6,136%)
PROBLEMA 11. - ¿Qué cantidad necesitamos imponer en una entidad bancaria que abona intereses del 4,5%
para que este sea suficiente para cubrir los gastos de un cierto negocio durante 10 años, sabiendo que el año
anterior ascendieron a 100000 euros y se prevé un aumento anual del 3%. (Suponga que los gastos se pagan
al final de cada año). (Sol: 924.356,61 euros)
PROBLEMA 12. - Determinar el valor actual de una renta de 10000 euros mensuales a percibir a final de cada
mes y 10 años de duración si el tanto efectivo anual es del 6%. (Sol: 907.243,22 euros)
PROBLEMA 13.- ¿cuál es el valor actual de una inversión que nos va a proporcionar 500 € dentro de cinco
años y 1000 € dentro de 10 años si el interés del mercado es del 5%? (Sol.:1.005,68)
PROBLEMA 14.- Dado el incremento en el precio de la vivienda, ¿cuánto tendría que ingresar al final de
cada año en una entidad bancaria que me paga unos intereses del 2,5% anual, para tener un capital de
100.000 € dentro de ocho años. (Sol.: 11.446,73)
PROBLEMA 15.- Si la rentabilidad que exige a sus inversiones es el 15% anual, ¿qué le interesa más,
cobrar ahora una cantidad de 1.000.000 de euros o 1.600.000 euros dentro de tres años? (Sol.: 1.600.000)
PROBLEMA 16.- Se invierte un capital de 1.000.000 de euros durante un año y medio al 1 % de interés
mensual. Se pide determinar el valor final del 1.000.000 de euros dentro de año y medio. (Sol.: 1.196.147,48)

18. 18
PROBLEMA 17 .- ¿Cuál es el valor actual de una inversión con la que vamos a obtener 6.000 € dentro de
cuatro años y 15.000 € dentro de 10 años, si el tipo de interés es del 4.75%? (13.972,64)
PROBLEMA 18.- Estamos intentando planificar un plan de ahorro para el futuro. En la actualidad
disponemos de una cuenta de ahorro con 100.000 euros al 7% de interés anual y, una cartera de valores
por 300.000 euros que obtiene una rentabilidad del 13% anual. Además queremos efectuar depósitos
anuales en la cuenta de ahorro por importe de 10.000 euros durante los próximos 5 años y de 20.000 euros
durante los cinco años siguientes. ¿Cuánto obtendremos al final de los diez años si se mantienen los
mismos tipos de interés? (392.387,01;1.018.370,22; total: 1.410.757,23)
PROBLEMA 19.- Con el capital obtenido al final del año 10 del ejercicio anterior, lo podremos colocar todo
durante los próximos 20 años al 10% ¿Qué cantidad podré retirar al final de cada uno de los años para
terminar con saldo cero al final de dichos veinte años? (165.707,01).

19. 1
Contenido
TEMA Nº 2: VALORACION Y SELECCIÓN DE PROYECTOS DE INVERSION. I ...............................................................2
2.1 CONCEPTO DE INVERSIÓN .......................................................................................................................................................................................2
2.2 LA DIMENSIÓN FINANCIERA DE LOS PROYECTOS ..........................................................................................................................................2
2.3 CLASIFICACION DE LOS PROYECTOS DE INVERSION....................................................................................................................................5
2.4 LOS PROYECTOS MUTUAMENTE EXCLUYENTES.............................................................................................................................................6
2.5 LA EVALUACIÓN DE INVERSIONES.......................................................................................................................................................................6
2.6 MÉTODOS USUALES DE SELECCIÓN DE INVERSIONES ..................................................................................................................................7
2.7 CRITERIO DEL PLAZO DE RECUPERACION .........................................................................................................................................................8
2.8 EL CRITERIO DEL VALOR ACTUAL NETO............................................................................................................................................................8
2.8.1 Ventajas e inconvenientes del criterio VAN ..................................................................................................................................................9
2.8.2 El significado económico del Valor Actual Neto.........................................................................................................................................10
2.9 EL PLAZO DE RECUPERACION DESCONTADO .................................................................................................................................................10
2.10 INDICE DE RENTABILIDAD...................................................................................................................................................................................10
2.11 VALOR FINAL NETO................................................................................................................................................................................................10
2.12 CRITERIO DE LA TASA INTERNA DE RENDIMIENTO: TIR ..........................................................................................................................11
2.12.1 Hipótesis de reinversión de los flujos intermedios de caja....................................................................................................................11
2.12.2 Tasa de rentabilidad múltiples .....................................................................................................................................................................11
2.12.3 Significado económico de la TIR .................................................................................................................................................................12
2.13 ANALOGIAS Y DIFERENCIAS ENTRE LOS CRITERIOS VAN Y TIR ...........................................................................................................12
2.13.1 Tasa de retorno sobre el coste de Fisher..................................................................................................................................................15
VALORACION Y SELECCIÓN DE PROYECTOS DE INVERSION. II................................................................................16
2.14 LA ORDENACIÓN DE PROYECTOS NO HOMOGÉNEOS ................................................................................................................................16
2.15 COMPARACIÓN DE PROYECTOS CON DIFERENTES DURACIONES.........................................................................................................16
2.15.1.- Proyectos con igual coste e igual VAN pero con diferente duración............................................................................................................16
2.15.2.- Proyectos con distinto coste, distinto VAN y diferente duración..................................................................................................................17
2.16 OTROS MÉTODOS DE SELECCIÓN ......................................................................................................................................................................19
2.17 COMPARACIÓN DE PROYECTOS CON DESEMBOLSOS DIFERENTES......................................................................................................19
2.17.1.- Proyectos con distinta inversión e igual duración y VAN .............................................................................................................................19
2.18 REEMPLAZO DE EQUIPOS INMOVILIZADOS..................................................................................................................................................21
2.19 RACIONAMIENTO DE CAPITAL ..........................................................................................................................................................................23
2.20 DISTRIBUCION TEMPORAL ÓPTIMA DE LAS INVERSIONES......................................................................................................................23
SELECCIÓN DE INVERSIONES EN REGIMEN DE INCERTIDUMBRE............................................................................24
2.21 INTRODUCCION........................................................................................................................................................................................................24
2.22 TRATAMIENTO DEL RIESGO ................................................................................................................................................................................24
2.23 AJUSTE DE LA TASA DE DESCUENTO...............................................................................................................................................................25
2.24 EQUIVALENTES DE CERTEZA..............................................................................................................................................................................25
2.25 ANÁLISIS DE LA SENSIBILIDAD..........................................................................................................................................................................26
2.26 VALOR DE LA INFORMACION..............................................................................................................................................................................28
2.27 ANALISIS DE ESCENARIOS ...................................................................................................................................................................................29
2.28 ANALISIS DEL PUNTO MUERTO..........................................................................................................................................................................29
2.29 ARBOLES DE DECISIÓN .........................................................................................................................................................................................31
2.30 SIMULACIÓN ESTADÍSTICA .................................................................................................................................................................................32
2.30.1 SIMULACIÓN DE MONTECARLO......................................................................................................................................................................32
2.31 ANÁLISIS PROBABILÍSTICO DE UNA SOLA INVERSIÓN ARRIESGADA .................................................................................................33
2.32 CÁLCULO DE LA ESPERANZA Y DE LA VARIANZA DEL VAN ..................................................................................................................35
2.33 COMPORTAMIENTO PROBABILISTICO DEL VALOR ACTUAL NETO ......................................................................................................36

20. 2
TEMA Nº 2: VALORACION Y SELECCIÓN DE PROYECTOS DE INVERSION. I
2.1 CONCEPTO DE INVERSIÓN
La definición más general que se puede dar al acto de invertir, es que, mediante el mismo, se produce el
cambio de una satisfacción inmediata y cierta a la que se renuncia, contra una esperanza que se adquiere y
de la cual el bien invertido es el soporte.
Del análisis de esta definición, podemos extraer los elementos básicos que se tienen que dar
necesariamente en el acto de invertir. En primer lugar, se dice que es un "acto", es decir un ejercicio de la
voluntad y como tal sólo puede ser realizado por una persona física o jurídica.
En segundo lugar, en este acto se produce la renuncia a una satisfacción inmediata y cierta, la cual puede
contemplarse en términos de un gasto inmediato. Es decir, toda inversión comporta un coste, que mediremos
habitualmente en términos monetarios.
En tercer lugar, como consecuencia de esa renuncia al consumo inmediato de una determinada cantidad de
dinero, se adquiere un determinado bien, que constituye el soporte físico de la inversión.
Y en cuarto lugar, en ese bien adquirido se fundamenta la esperanza de obtener en un futuro unos ingresos
mayores al gasto inmediato soportado.
En definitiva, los elementos que permiten definir un acto como inversión, son:
1. - Una persona, física o jurídica que invierta.
2. - Un objeto en el que se invierta.
3. - El coste que supone la adquisición del objeto soporte de la inversión.
4. - La esperanza de poder obtener una contrapartida futura superior al coste del bien adquirido.
Una de las funciones del director financiero es la toma de decisiones de inversión o presupuesto de capital,
estas decisiones de inversión son las más importantes con las que se tiene que enfrentar el Director Financiero
ya que afectan a todos los Departamentos de la empresa. Al conjunto formado por la inversión principal más la
inversión complementaria en activo circulante, lo denominaremos proyecto de inversión.
La valoración y selección de los proyectos de inversión se realizarán en un principio en condiciones de
certeza, es decir, suponiendo que los valores futuros de las variables que definen los proyectos son
perfectamente conocidas. La premisa básica del proceso consistirá en considerar una independencia
absoluta del tratamiento de la inversión con respecto al de la financiación, es decir, por una parte,
valoraremos el activo con independencia del pasivo asociado a ellas; y por otra parte valoraremos el pasivo
con independencia del activo que financien.
Otra hipótesis simplificadora consiste en hacer coincidir la corriente de renta con la de tesorería, es decir,
considerar a todo ingreso como cobrado y a todo gasto como pagado, la existencia de un sólo producto y la
inexistencia de variaciones en los stocks. Esta hipótesis no contempla el uso comercial del crédito tanto por
el comprador como por el vendedor y, las políticas de stocks seguidas por las empresas, provocando en la
práctica un desfase entre los cobros reales por ventas (activos corrientes) y, los pagos reales por compras y
gastos (pasivos corrientes). Este desfase financiero se denomina “necesidades de capital corriente” que
deben ser financiadas con recursos permanentes, variando su cuantía de unos años a otros y
recuperándose al final de la vida del proyecto de inversión.
2.2 LA DIMENSIÓN FINANCIERA DE LOS PROYECTOS
Para definir financieramente (monetariamente) a los proyectos de inversión y financiación, supondremos la
creación, explotación y liquidación de una empresa, al objeto de comprobar los movimientos de tesorería
que definirán a la correspondiente inversión y financiación.
El primer paso para la creación de una empresa es acudir al mercado financiero en busca de los recursos
financieros necesarios para nuestra inversión. Supongamos que necesitamos Q0 unidades monetarias, las
cuales podemos conseguir de ciertos accionistas (RP) y de ciertos prestamistas (RA) de forma que: Q0 = RP
+ RA.

21. 3
Estos recursos estarán al principio materializados en la tesorería, hasta el momento de adquirir los activos
necesarios, es decir, invertir. Inversión que se concreta en la adquisición en el mercado de bienes
productivos (Q0) y en el mercado de bienes y servicios (materias primas, mano de obra, suministros). Una
vez adquiridos estos activos fijos y circulantes podemos empezar a funcionar.
En primer lugar pondremos en marcha el ciclo corto o de explotación de la empresa. Este ciclo nos
determinará unos intercambios monetarios anuales entre la empresa y el mercado de bienes y servicios,
consistentes en el cobro de las ventas realizadas y el pago de los gastos de explotación, el resultado de
estos intercambios se denomina “flujos netos de caja: FNC”. Por otra parte, al habernos financiado con
ciertos capitales propios y ajenos nos obligará en el futuro a realizar una serie de pagos en concepto de
retribución de esos capitales en forma de dividendos (D) y costes financieros o intereses (CF), así como a
una devolución de los recursos ajenos en forma de cuotas de amortización financiera (CAF) y devolución de
los recursos propios en caso de liquidación de la empresa. Estos intercambios se producirán en el mercado
financiero.
Estos FNC de cada año deben ser suficientes para:
- Remunerar los recursos financieros: D + CF
- Devolución de los recursos financieros: CAF + RP
- Deben dejar a la empresa un excedente o ganancia neta en tesorería: Ts
Por tanto: FNC = D + CF + CAF + RP + Ts.
Por último los sucesivos ciclos de explotación depreciarán nuestro activo fijo hasta que llegue un momento
en que quedará obsoleto, vendiéndolo en el mercado de bienes productivos usados y obteniendo una
cuantía monetaria que denominaremos valor residual (VR), en el momento final del proyecto, momento (n).
Desde un punto de vista financiero, es decir monetario, cualquier proyecto de inversión viene definido por
las siguientes variables:
Capital invertido o coste inicial: Q0 : Representa el volumen de fondos que la empresa destina a la
realización de una inversión. Cuando la realización de la inversión implica la utilización de capitales
desplazados en el tiempo, se procederá a actualizar esos pagos al momento inicial con el fin de considerar
al capital invertido como una única salida de caja. Esta forma de actuar evita a veces complicaciones
adicionales en el cálculo de la TIR. Como componentes del coste inicial, tenemos:
a) Compra de terrenos, edificios, pagos por estudio, maquinaria, pagos por montaje y puesta en marcha de
las instalaciones (dentro de esta apartado incluiremos los costes financieros del capital invertido
correspondiente al período de montaje, pero no los correspondientes al período de explotación).
b) Pagos por formación de personal.
c) Variaciones del capital corriente.
Flujos netos de caja: Qi: Es la diferencia entre la corriente de cobros y de pagos del período que
vengamos considerando. También se conoce como cash-flow de tesorería, y representa las disponibilidades
financieras de la empresa. Este concepto puede descomponerse en:
a) cash-flow operativo o de explotación, que es el determinado por el ciclo corto o de explotación de la
empresa.
b) cash-flow no operativo o extraordinario de pasivo, determinado por las variaciones de tesorería a que da
lugar el pasivo empresarial (pago de su retribución, amortizaciones financieras, incrementos de pasivo,
etc.)
c) Cash-flow no operativo o extraordinario de activo, determinado por la compra-venta de activos, así como
por los cobros y pagos derivados de operaciones de activo no estrictamente de explotación.
En la valoración de inversiones imputaremos a la dimensión financiera del proyecto tanto el cash-flow
operativo o de explotación, como el extraordinario de activo; de forma que el caso más simple corresponde
a un proyecto con un flujo neto de caja inicial, extraordinario y de activo, correspondiente al capital invertido
del proyecto, posteriormente tendremos diferentes flujos netos de caja por explotación a obtener a final de
cada período, Los cuales provienen del funcionamiento (explotación) de la inversión; y por último,
tendremos un flujo neto de caja final, extraordinario y de activo, generado por la venta en el momento final
del proyecto de los activos en que se materializó la inversión inicial.

22. 4
La realización de un proyecto de inversión modifica los flujos de caja globales actuales y futuros de la
empresa. Por tanto, para evaluar una inversión, deben cuantificarse estos cambios en los flujos de caja de
la empresa y determinar si añaden o no, valor a la empresa. Por eso, los flujos inherentes a un proyecto
deben ser de carácter incremental. Esto significa que los flujos deben ser todos y sólo los que aparecen
como resultado de aceptar el proyecto. Dicho de otra forma, sólo las salidas y entradas de caja adicionales,
ocasionadas directamente por la aceptación del proyecto, o que deban ser imputadas al mismo, han de ser
tenidas en cuenta. Todos los flujos producidos antes de la aceptación del nuevo proyecto (costes hundidos)
o que se vayan a producir en el futuro a consecuencia de los proyectos ya aceptados deben ser olvidados a
la hora de establecer los flujos del proyecto en estudio.
Estos flujos netos de caja se producen de forma continua en el tiempo, por comodidad en el cálculo
suponemos una periodificación de forma discontinua La periodificación suele referirse a un horizonte
temporal anual, por ser ésta la duración normal del ejercicio empresarial.
Valor residual: VR: Es el precio de venta en mercado de un activo propio y en un momento determinado.
La evolución del valor residual es creciente, como ocurre con los bienes sometidos a revalorización
(terrenos), o bien decreciente, para los bienes depreciables (sometidos al proceso de amortización). En el
momento de la venta del activo, se originarán unos incrementos o decrementos de patrimonio (plusvalías o
minusvalías). El incremento/decremento de patrimonio es una ganancia/pérdida no operativa, generada por
la obtención de un valor residual mayor/menor al valor contable en el momento de la venta. Esto tiene
importancia a la hora de evaluar los impuestos a pagar por el valor residual, ya que si se cumplen
determinadas condiciones a los incrementos/decrementos de patrimonio se consideran como
incrementos/decremento de la renta de la sociedad y por tanto darán lugar a un pago por impuestos o bien
a un ahorro por el mismo concepto.
El horizonte temporal de valoración - n : En algunas ocasiones su valor viene predeterminado por el tipo
de inversión (a plazo fijo) o por un deseo expreso de la gerencia. Cuando no ocurre esto, tenemos que
considerar en los activos productivos los conceptos de “vida técnica” y “vida económica”. Siendo la vida
técnica el tiempo que el activo en cuestión va a funcionar proporcionando los estándares de calidad exigidos
al producto; y por vida económica el tiempo durante el cual el activo va a ser rentable. La vida económica
será igual o menor que la vida técnica, siendo aquella la duración que nos interesará utilizar como
referencia.
La tasa de actualización: k : La tasa de actualización hace comparables, en cuanto homogeniza respecto
al tiempo, los valores de los flujos netos de caja de todo proyecto de inversión, que se obtienen en épocas y
cuantías determinadas y diferentes. Constituye la rentabilidad mínima exigida por el empresario para un
proyecto de inversión. Esta tasa de actualización debe a su vez permitir atender los costes en que la
empresa incurrirá para obtener los recursos con los que ha de financiar el proyecto de inversión.
En el supuesto de que no existan restricciones de recursos financieros, la tasa óptima de actualización
vendrá dada por el llamado coste explícito medio, ponderado e incremental de capital, o lo que es igual,
el coste efectivo de los recursos financieros asignados al proyecto de inversión en cuestión.
Se entiende por coste explícito “aquél tipo de interés efectivo que la empresa deberá pagar por el uso de
sus recursos financieros”. Ahora bien, no es el coste actual de capital, sino el posible coste de los recursos
incrementales que financiarán al nuevo proyecto de inversión, es decir el denominado coste explícito e
incremental de capital. Además, el incremento de los recursos anteriores estará formado por varias fuentes
financieras, cada una con su coste particular, por tanto deberá determinarse una media ponderada en
función de los distintos costes y distintos volúmenes que componen el incremento de pasivo, es decir,
deberemos hablar de un “coste medio ponderado e incremental de pasivo”. Aplicamos la siguiente fórmula
para la determinación del CCMP:
ik
CACP
CA
ek
CACP
CP
CCMP



 ; donde ke y ki son los costes financieros de los capitales propios y ajenos.
La dimensión financiera de un proyecto de inversión, teniendo en cuenta la periodifcación anual, quedará de
la siguiente forma:
0 1 2 3 . . . . . . ………. . .n
-Q0 Q1 Q2 Q3 . ……….. . . . . . .Qn

23. 5
Toda inversión habrá de cumplir dos condiciones previas para su realización:
a) Condición de posibilidad o economicidad del proyecto: Qi > 0 y Qi Q  0 0
b) Condición de efectuabilidad, también llamada de rentabilidad financiera: rentabilidad de la inversión >
coste del capital.
Cálculo de los distintos flujos netos de caja:
Períodos T = 0 T = 1,2,3,.., años T= n
+ Cobros del periodo +C +C
- Pagos costes variables -P -P
- Pagos costes fijos -P -P
= FNCai (antes de impuestos) = FNCai = FNCai
- Amortización -A -A
= Base Imponible = B.I. = B.I.
- Impuestos (t = % s/BI) -I -I
= BDI (beneficio después de impuestos) = BDI = BDI
+ Amortización +A +A
= FNCdi (después de impuestos)
Pago inversión - Inversión
Necesidades de capital corriente
Valor residual +VR
= Cash Flow -Q0 Q1,2,….n Qn
Siendo:
- C = cobros del período
- P = pagos del período
- FNCai = flujo neto de caja antes de aplicar los impuestos, se obtiene por diferencia entre los cobros y
los pagos de período.
- A = es la cuota anual correspondiente al gasto de amortización. En el cuadro aparece en primer lugar
restando, ya que, es un gasto fiscalmente deducible, por tanto, su inclusión produce un ahorro de
impuestos.
- B.I. = es la base imponible, sobre dicha base imponible se aplica la tasa impositiva.
- I = es el resultado de aplicar la tasa impositiva sobre la base imponible. Aparece con signo menos
porque representa un pago.
- BDT = es el beneficio después de pagar los impuestos.
- A = En esta línea, la amortización está sumando, porque al no ser un pago, no se incluye en el cálculo
del cash flow.
- Q0 = es el cash flow correspondiente al momento inicial. Aparece con signo negativo ya que en el
momento inicial el único flujo de caja corresponde al pago de la inversión.
- VR = es el valor residual, aparece con signo positivo, ya que representa el ingreso que se obtendrá por
la venta del activo, una vez finalizada la inversión.
- Q1.2…n. = representan los distintos cash flows anuales.
2.3 CLASIFICACION DE LOS PROYECTOS DE INVERSION
Las inversiones se pueden clasificar desde diferentes puntos de vista. Atendiendo a la función de las
inversiones en el seno de la empresa tenemos:
a) Inversiones de “renovación o reemplazo”: son las que se llevan a cabo con el objeto de sustituir un equipo o
elemento productivo antiguo por otro nuevo, con el fin de reponer el beneficio erosionado por el desgaste o la
obsolescencia del equipo.
b) Inversiones de “expansión”, que son las que se efectúan para hacer frente a una demanda creciente, son las
que presentan un mayor grado de incertidumbre, que es todavía mayor cuando se trata de nuevos productos.
c) Inversiones de “modernización o innovación”, que son las que se hacen para mejorar los productos
existentes o para la puesta a punto y lanzamiento de productos nuevos.

24. 6
d) Inversiones obligadas por exigencias legales, por seguridad, por presión del personal y conservación del
medio ambiente: estas inversiones hay que realizarlas sin tener en cuenta la rentabilidad, como por ejemplo:
salidas de emergencia, sistemas contra incendios y contra robos, eliminación de residuos, depuración de
aguas, etc. De hecho, más que de inversiones se trata de gastos necesarios, aunque estos gastos se activen
para su posterior amortización. Sin embargo, aunque no se calcule la rentabilidad de estas inversiones
necesarias, hay que formular los proyectos correspondientes a fin de cuantificar los recursos requeridos, ya que
todos los proyectos de inversión analizables con criterios de rentabilidad deberán asumir una parte alícuota de
estos gastos necesarios, a fin de conservar la rentabilidad global de la empresa.
Atendiendo a la relación que guardan entre sí las inversiones, éstas se pueden clasificar en: complementarias,
sustitutivas e independientes. Dos o más inversiones son complementarias cuando la realización de una de
ellas facilita la realización de las restantes. Si la realización de una inversión exige la realización de otra u otras,
se habla entonces de inversiones acopladas. Varias inversiones son sustitutivas cuando la realización de una
de ellas dificulta la realización de las restantes; si la aceptación de una o varias inversiones excluye
automáticamente la realización de las restantes, se dice que las inversiones son incompatibles o mutuamente
excluyentes. Las inversiones son independientes cuando no guardan ninguna relación entre sí.
Las relaciones más frecuentes y de mayor interés son las que se refieren a proyectos independientes y
proyectos mutuamente excluyentes: Los proyectos independientes hay que analizarlos, cada uno de por sí,
teniendo en cuenta todos los flujos de salida y entrada inherentes al proyecto como tal. En los proyectos
mutuamente excluyentes lo primero que hay que ver es si realmente lo son. La manera de hacerlo, en el
caso general en que los proyectos sean más de dos, es comprobar que ninguna decisión futura resultará
afectada por el hecho de aceptar uno cualquiera de estos proyectos, rechazando los restantes.
2.4 LOS PROYECTOS MUTUAMENTE EXCLUYENTES
Comprobado que dos o más proyectos son excluyentes entre sí, para analizar cuál de ellos es preferible
bastará con tomar en consideración los flujos diferenciales, calculados a partir de aquello en que un
proyecto difiere de otro y prescindiendo de aquello que le es común, es decir, de aquello que no varía por el
hecho de elegir uno u otro de los proyectos. Por ejemplo: una empresa contempla la elección entre construir
un nuevo almacén, adquirirlo ya construido, alquilarlo o tomarlo en leasing. La elección de una de estas
cuatro opciones excluye todas las demás. Pero cualquiera que sea la que se elija, ni la cifra de ventas, ni el
coste de producción, ni los gastos de estructura resultan afectados por la elección. Luego nada de esto
debe entrar en el análisis. Los flujos a considerar, y que permitirán establecer los diferencias, serán
solamente los relativos al coste y tiempo de construcción, en la primera opción; al precio de compra, en la
segunda; a la amortización y al valor residual en ambas; a los alquileres, en la tercera opción; y a las cuotas
de leasing y a la opción de compra, en la cuarta.
Otro ejemplo de proyectos mutuamente excluyentes: una empresa que dispone de un equipo cuya
capacidad de producción no está saturada, ante un aumento consolidado de la demanda, contempla la
elección entre adquirir un nuevo equipo de mayor productividad o aumentar la plantilla trabajando en el
antiguo equipo. O también: atender un aumento temporal de demanda, comprando a terceros o haciendo
horas extraordinarias.
2.5 LA EVALUACIÓN DE INVERSIONES
La decisión óptima de inversión debe ser tomada en orden a la influencia que los valores representativos de
la dimensión financiera del proyecto tengan sobre el objetivo financiero. Para ello, tenemos que resumir en
un índice toda la información financiera expresada en la inversión.
Este índice puede expresarnos liquidez, rentabilidad, beneficio social, etc. pero deberemos aceptar aquella
unidad de medida que mejor refleje la contribución del proyecto al objetivo financiero de la empresa que es
“la maximización del valor en mercado de la empresa para los accionistas”, lo cual pasa en primer lugar por
la maximización de la rentabilidad de los activos. Se acepta que el criterio de rentabilidad es el más
adecuado por cuanto que todo incremento de la misma, presupone, automáticamente, un incremento del
valor en mercado de la empresa para los accionistas.
Por lo que respecta al momento en que debe evaluarse, cabe distinguir entre dos situaciones extremas:

25. 7
a) Una situación a priori o realizada antes de acometer el proyecto y cuyo objetivo reside en estudiar la
conveniencia de llevarlo a cabo.
b) Una situación a posteriori o realizada después de finalizar el proyecto de inversión, su objetivo en
controlar la rentabilidad de la inversión una vez terminadas.
Entre estas dos situaciones, cabría considerar una evaluación continua a realizar por la empresa al objeto
de controlar en cada momento, la realización del proyecto y poder tomar medidas correctoras de las
posibles desviaciones.
Las condiciones ante las cuales se evalúa pueden variar ante uno u otro caso. Así, en la evaluación a
posteriori tendremos siempre unas condiciones de certeza, es decir, conoceremos exactamente los valores
que ha tomado cada variable financiera. En la evaluación a priori tendremos dos condiciones extremas poco
frecuentes: la certeza y la incertidumbre.
 La certeza: los valores estimados para cada variable coincidirán con los valores que realmente se
obtengan.
 La incertidumbre: tendremos un desconocimiento total de los valores futuros de cada variable.
Entre estas condiciones límite puede distinguirse una situación intermedia denominada riesgo, en la cual se
conocen en términos de probabilidad los valores futuros de la variable. El tratamiento que se le da a una
inversión ante unas condiciones de incertidumbre reside en reducirla a una situación de riesgo, ya que en
este caso, la estadística proporciona las herramientas adecuadas para la evaluación. El paso de una
situación a otra puede hacerse con ayuda del concepto de probabilidad subjetiva y, en cualquier caso, se
aplicarán los mismos criterios de evaluación, es decir idénticos índices de medida de rentabilidad.
Relacionado con la evaluación están la “comparación” y “selección” de inversiones. Con la comparación se
pretende establecer una jerarquía y orden de preferencias entre los diferentes proyectos objeto de la
comparación. Por el contrario la selección de inversiones es un problema de elección en el que se pretende
escoger el mejor proyecto o grupo de proyectos.
Ahora bien, antes de cualquier problema de selección, comparación o evaluación de proyectos de inversión,
se debe realizar una correcta determinación de cada una de las variables determinantes de la dimensión
financiera del proyecto (capital invertido, valor residual, flujos netos de caja, horizonte temporal de
valoración y tasa de actualización). Esta determinación comporta dos fases netamente diferenciadas, en
primer lugar una definición de los componentes de cada variable, para pasar en segundo lugar a la previsión
de sus futuros valores. Hemos estudiado en el apartado anterior la primera fase, ya que, la segunda
requiere numerosas investigaciones y estudios destinados a precisar las características de los proyectos,
así, serán necesarios estudios previos de marketing, técnicos, humanos, jurídicos, fiscales y financieros.
2.6 MÉTODOS USUALES DE SELECCIÓN DE INVERSIONES
Una vez estudiados los distintos aspectos que afectan a la toma de decisiones de inversión, vamos a examinar
distintos criterios que nos permitan clasificar las inversiones en proyectos aceptables o inaceptables. Los
criterios más importantes para tomar esa decisión son:
a) criterio del plazo de recuperación o pay-back.
b) criterio del valor actual neto VAN.
c) plazo de recuperación descontado.
d) criterio de la tasa interna de rentabilidad TIR.
e) índice de rentabilidad.
f) valor final neto.
Al comparar varios criterios de presupuesto de capital, hay que tener en cuenta que la decisión óptima debe
respetar cuatro características:
1. - Considerar todos los flujos de caja.
2. - Descontar los flujos de caja al coste de oportunidad del capital apropiado y determinado por el mercado.
3. - A partir de un conjunto de proyectos de inversión mutuamente excluyentes seleccionar aquel que maximice
el valor de mercado de las acciones.

26. 8
4. - Considerar cada proyecto de manera independiente. Dado que los valores actuales netos se miden en
unidades monetarias, es posible sumarlos. Esta característica se conoce como principio de aditividad del
valor.
Para estudiar los distintos criterios de selección, vamos a partir de unos supuestos simplificadores de la realidad
para posteriormente ir abandonando dichos supuestos, estos son:
1. - Se considera dado el coste de oportunidad del capital
2. - Se tiene absoluta certeza de la corriente de cobros y pagos que definen un proyecto de inversión.
3. - Se considera una situación económica de estabilidad de precios (ausencia de inflación) y un sistema
impositivo que no grava los beneficios de la empresa.
2.7 CRITERIO DEL PLAZO DE RECUPERACION
El plazo de recuperación es el número de años que la empresa necesita para recuperar su inversión inicial a
partir de los flujos netos de caja. Aunque el plazo de recuperación es fácil de calcular, puede conducir a
decisiones erróneas ya que, este método ignora los FNC que se reciben después del plazo de recuperación.
Otro punto débil de este criterio es el de no considerar el valor del dinero a través del tiempo. La utilización de
este criterio se fundamenta en los siguientes aspectos:
1. - El grado de incertidumbre que afecta a los FNC que se esperan obtener a partir del cuarto o quinto año de
vida del proyecto.
2. - La necesidad de tener liquidez por parte de las empresas ya que, un plazo de recuperación más corto
permite a la empresa utilizar los fondos obtenidos para satisfacer otras necesidades.
3. - Por ser un criterio fácil de aplicar, muchas empresas lo utilizan cuando tienen que realizar muchas
decisiones pequeñas de inversión ya que, los costos de usar otros criterios más complejos pueden ser
superiores a los beneficios derivados de elecciones quizás mejores entre proyectos competitivos.
4. - Permite mostrar el tiempo durante el cual la inversión original estará en riesgo, es decir, el plazo de
recuperación se usa como un indicador del riesgo. Esto hace que este criterio sea utilizado por grandes
empresas que realizan inversiones en países con inestabilidad política y económica.
5.- Las empresas pueden fijar una fecha tope para recuperar la inversión, se eligen aquellas que se recuperan
dentro del plazo independientemente que el VAN sea positivo o negativo.
Cuando los flujos netos de caja son constantes Q1=Q2=.... =Qn= Q, utilizamos la expresión: PR = Q0/Q
2.8 EL CRITERIO DEL VALOR ACTUAL NETO
Definido el criterio de rentabilidad como el más adecuado para la evaluación de inversiones y, teniendo en
cuenta que los cash-flows nos representan las ganancias (rentabilidades) anuales derivadas del
funcionamiento del activo, es decir, del funcionamiento de la inversión, una forma de determinar la
rentabilidad del proyecto consistirá en el cálculo de la suma de todos los cash-flows anuales, lo cual nos
dará la ganancia total bruta de la inversión, de forma que al restarle el coste de ésta, el capital invertido, nos
dará la ganancia total neta.
VAN = - QO + Q1 + Q2 +……..+ Qn
En la fórmula anterior no se ha considerado que el dinero no tiene el mismo valor a lo largo del tiempo, es
decir, no tiene en cuenta a la actualización, de forma que suma cantidades no homogéneas de dinero. Por
tanto, debemos referir a un determinado momento todas las unidades monetarias, pudiendo entonces ser
sumadas. Tomamos como momento de tiempo el momento presente, ya que todo inversor sabe lo que
valen exactamente las pesetas de hoy y tiene dudas razonables sobre el valor de las pesetas de mañana.
Por tanto, la fórmula anterior quedaría:
n
k)(1
nQ
.........
2
k)(1
2Q
k)(1
1Q
0QVAN






Donde 1/(1+k) es el factor de actualización. Siendo k la tasa de actualización, nos expresa la rentabilidad
mínima exigida a las inversiones, ya que es precisamente éste valor el que hace que los capitales sean
homogéneos en el tiempo.

27. 9
En consecuencia, el VAN de un proyecto de inversión nos determina la rentabilidad (ganancia) total neta
actualizada al momento inicial. Nos proporciona la ganancia total de la inversión por cuanto que hemos
sumado todas las ganancias parciales (cash-flows anuales) para su determinación, así mismo, nos
proporciona la ganancia neta pues supone amortizado financieramente el pasivo que posibilitó a la inversión
(Q0), y por último esta ganancia neta está referida a unidades monetarias del momento inicial (pues hemos
actualizado).
Podemos establecer las normas de decisión para los proyectos de inversión: Se aceptan los que presentan
un VAN positivo, se rechazan los que presentan un VAN negativo. Si el VAN es nulo, nos indica la
indiferencia del proyecto en cuanto al objetivo perseguido (un proyecto con VAN = 0 se podría realizar ya
que permite recuperar la inversión efectuada y remunerar a un k% a los capitales invertidos de acuerdo al
riesgo soportado, y aunque no genera un excedente financiero y, por tanto, un incremento en el valor de
mercado de la empresa, sí que le permite crecer y posicionarse mejor en el mercado). Cuando tengamos
dos proyectos de inversión con diferentes VAN, en principio el mejor será el de mayor VAN.
La fórmula anterior es la que utilizaremos normalmente para obtener el VAN, ahora bien, en determinadas
circunstancias cambiaremos la formulación anterior:
a) Supuesto que la tasa de actualización sea distinta para cada período, ki, es decir, en el supuesto que el
inversor cambie periódicamente de deseo mínimo de rentabilidad a exigir a las inversiones, tendríamos:
VAN Q
Q
k
Q
k k
Qn
k k kn
  


 
 
  
0
1
1 1
2
1 1 1 2 1 1 1 2 1( ) ( )( )
.........
( )( )... ( )
b) Supuesto que la tasa de actualización fuese constante para todo el horizonte temporal de la inversión,
así como que también se mantuviese constante el valor de los flujos netos de caja de cada período,
tendríamos:
VAN Q Q
k k k
n Q Qank  



 

  



0
1
1
1
1
2
1
1
0
( ) ( )
......
( )
c) Supuestas las condiciones anteriores, el horizonte temporal del proyecto es infinito:
VAN Q Q
k
  0
1
2.8.1 Ventajas e inconvenientes del criterio VAN
El criterio VAN presenta las siguientes ventajas:
1. - La sencillez de cálculo que requiere su aplicación.
2. - La homogenización de todos los flujos de caja a un mismo momento de tiempo (inicial).
3. - El criterio del VAN cumple el principio de aditividad del valor.
4. - El VAN del proyecto es exactamente igual al incremento de patrimonio de los accionistas.
Los inconvenientes en el VAN se producen como consecuencia de que este método supone que los flujos
netos de caja positivos (al ser potencialmente rentables) son reinvertidos a una tasa de rendimiento k' que
coincide con el coste de oportunidad del capital, y que Los flujos de caja negativos son financiados con unos
recursos cuyo coste también es k'. Al considerarse explícitamente las reinversiones, todo proyecto queda
definido por otro equivalente, determinado por una salida de caja en el momento inicial (Q0) y una sola entrada
en caja en el momento final (numerador de la siguiente expresión). En efecto, puede comprobarse que cuando
la tasa de reinversión k' es igual a k se verifica la siguiente identidad:
 
n
k)(1
nQ.....
2n
k´)(12Q
1n
k´11Q
0QVAN







Sin embargo, el futuro presentará a la empresa un mercado financiero ciertamente diferente del actual y
también es posible que se presenten oportunidades de inversión con rendimientos distintos de los que se
obtienen actualmente en el mercado financiero. Por tanto, si el tipo de reinversión o financiación fuera diferente
de k', ya no se daría tal identidad y el valor actual neto ex-post sería distinto del valor actual neto ex-ante.

28. 10
2.8.2 El significado económico del Valor Actual Neto
La tasa óptima de actualización debe ser la exigencia mínima de rentabilidad para las inversiones por parte
del inversor, o en su defecto, el coste de capital medio ponderado de los recursos financieros inmovilizados
en el proyecto. Una vez obtenido el VAN, éste nos proporciona la rentabilidad total neta del proyecto,
actualizada al momento inicial. Esta ganancia neta es lo que quedaría en la empresa una vez que:
1. - Se han pagado los gastos de explotación, ya que en el numerador sólo incluimos los cash-flows, es
decir, las ganancias de activo una vez pagados los gastos de funcionamiento del mismo.
2. - Se ha amortizado financieramente el pasivo que posibilitó la inversión Q0.
3. - Se ha pagado la retribución del pasivo, lo cual aparece en la fórmula al considerar una actualización al
coste medio ponderado de capital de la inversión k0.
El VAN de un proyecto es el excedente que deja después de satisfacer las exigencias de los capitales
ajenos y de los propios. Como los capitales de deuda no pueden exigir ni esperar más de lo
contractualmente establecido, este excedente se reparta o no, es de los accionistas. El VAN es, pues, un
regalo del proyecto para los accionistas. El VAN es el valor creado para los accionistas. Como este valor ha
sido calculado al coste ponderado de capital que comprende el coste de los fondos propios de acuerdo con
lo que los accionistas desean y esperan, es decir, calculado a precios de mercado, podemos concluir que, si
los flujos del proyecto se realizan tal como se ha previsto, la aceptación y realización del proyecto significa
que el valor de mercado de los fondos propios (manteniéndose constantes los demás proyectos), aumenta,
en el momento inicial del proyecto, en un importe igual al VAN del proyecto.
2.9 EL PLAZO DE RECUPERACION DESCONTADO
Es el número de años que se necesitan para que el valor actual neto de los flujos de caja hasta entonces
generados sea igual al desembolso de la inversión:

 

p
1t tk)(1
tQ
0Qsiendo0;=
)
t
k+(1
Qt
p
1=t
+Q0-=VAN
En donde -p- es el plazo de recuperación. Sin embargo el plazo de recuperación descontado sigue adoleciendo
de un importante defecto: el de no tener en cuenta los flujos netos de caja generados por la inversión a partir de
dicha fecha.
2.10 INDICE DE RENTABILIDAD
Es el cociente entre la suma de los flujos de caja descontados al coste de oportunidad del capital y la inversión
inicial.
Q0
)
t
k+(1
Qt
n
1=t
=IR

Se deben aceptar los proyectos cuyo índice de rentabilidad sea superior a la unidad.
2.11 VALOR FINAL NETO
Expresa la comparación entre los flujos netos de caja y el coste de la inversión con base a sus valores futuros a
la terminación del proyecto. Tanto los FNC como la inversión van creciendo hasta la terminación del proyecto al
coste de oportunidad del capital.
)
n
k+(1Q0-)
t-n
k+(1Qt
n
1=t
=VFN 
Cuando el valor terminal neto se descuenta al momento actual al coste de oportunidad del capital, obtenemos el
valor actual neto. De esta forma, para proyectos de igual duración el valor final neto nos proporciona la misma
ordenación de proyectos que el valor actual neto.

29. 11
2.12 CRITERIO DE LA TASA INTERNA DE RENDIMIENTO: TIR
La tasa interna de rentabilidad de una inversión se define como la tasa de descuento que iguala a cero el valor
actual neto de toda la serie de flujos netos de caja asociados con el proyecto. Para hallar la TIR (r) del
proyecto, debemos utilizar la siguiente expresión:
0=
)
n
r+(1
Qn
+....+
)
2
r+(1
Q2
+
r)+(1
Q1
+Q0-=VAN
La TIR se denomina así porque es una rentabilidad interna del proyecto, calculada independientemente del
coste de oportunidad del capital de la empresa.
La solución de esta ecuación implica normalmente un proceso de prueba y error. Este procedimiento consiste
en calcular el valor actual de los flujos netos de caja de la inversión usando una tasa de interés arbitrariamente
seleccionada. Después se compara el valor presente obtenido con el costo de la inversión. Si el valor presente
es más alto que la cifra de coste, se toma una tasa de interés más alta y se repite de nuevo el procedimiento. A
la inversa si el valor presente es más bajo que la cifra de coste, se disminuye la tasa de interés y se repite el
procedimiento. Se continua hasta que el valor presente proveniente de la inversión sea aproximadamente igual
a su coste.
Cuando tenemos que establecer una ordenación para el presupuesto de capital sobre la base de la tasa interna
de rendimiento, el criterio a seguir consiste en aceptar un proyecto de inversión si el coste de oportunidad del
capital es menor que la tasa interna de rentabilidad, dándose prioridad a aquéllas cuya tasa interna de
rendimiento sea mayor.
2.12.1 Hipótesis de reinversión de los flujos intermedios de caja
Uno de los inconvenientes que presenta el criterio TIR, al igual que el criterio VAN, es suponer que los flujos
netos de caja son reinvertidos mientras dure la inversión, a un tipo de interés igual a r' y que los flujos netos de
caja negativos son financiados con capital cuyo coste es también igual a r'. Esto presupone implícitamente
que, r'= r, es decir, que la tasa de reinversión de los flujos netos de caja del proyecto es igual a la rentabilidad
relativa del proyecto.
Esta hipótesis de reinversión o financiación de los flujos intermedios de caja implica, por una parte, que la
empresa puede obtener de los activos que constituyen el soporte físico de la reinversión una rentabilidad igual
a la del proyecto originario, aspecto éste, que se contradice con el calificativo de "interno" que se le asigna a la
tasa de rentabilidad. Por otra parte, se trata de una hipótesis pesimista en lo que respecta a la financiación de
los flujos netos de caja negativos, se va a efectuar a un coste superior a lo que cuesta a la empresa financiar,
en términos de promedio, el resto de su actividad productiva, k.
En efecto, comprobamos que cuando r'= r se verifica la siguiente identidad:
)
n
r+(1
Qn+.....+)
2-n
r+(1Q2+)
1-n
r+(1Q1
=
)
n
r+(1
Qn
+....+
r)+(1
Q1
+Q0=0=VAN


Por lo tanto, si el tipo de reinversión o financiación r' fuera diferente de r, ya no se daría tal identidad y la tasa
de rendimiento efectivamente obtenida sería diferente de la tasa de rendimiento teórica calculada, aún en el
supuesto de que los valores de Q0 y Qj para j=1,2,..n coincidieran exactamente con los valores estimados.
2.12.2 Tasa de rentabilidad múltiples
Cuando en una inversión es positivo el signo de todos los flujos netos de caja Qj, y negativo el signo del
desembolso inicial Q0, se dice que es una inversión simple. Cuando el desembolso inicial Q0 es negativo y
algunos de los flujos netos de caja son también negativos mientras que otros son positivos, se dice que la
inversión es no simple. Lo anterior implica que bajo ciertas circunstancias, se pueda usar diferentes valores
de -r- para resolver la ecuación:

30. 12
0=
)
n
r+(1
Qn
+....+
)
2
r+(1
Q2
+
r)+(1
Q1
+Q0=VAN
Esta ecuación es un polinomio de grado -n- y según la Regla de los Signos de Descartes pueden haber tantas
raíces positivas como cambios de signo existen en los valores de Q0 y Qj.
Si la inversión es simple (para las que existe un único cambio de signo) tienen siempre una única solución
positiva. Si la inversión es no simple pueden existir varias tasas de rendimiento interno positivas o puede no
existir ninguna tasa de rendimiento real. Cuando se presenta este caso decimos que el método TIR no es
“consistente” porque conduce a resultados que no concuerdan con la lógica o al menos no concuerdan con el
concepto intuitivo que tenemos del tipo de interés.
Cuando se nos presente el caso de inversiones no simples con varias tasas de rentabilidad o en las que no
exista tasa de rentabilidad real, usaremos el criterio del VAN a la hora de establecer una ordenación para el
presupuesto de capital.
2.12.3 Significado económico de la TIR
La TIR como hemos dicho determina la rentabilidad relativa del proyecto de inversión. Esta medida de
rentabilidad no es sobre el capital invertido inicialmente, sino que proporciona la rentabilidad relativa anual
bruta del proyecto de inversión, es decir, esta rentabilidad incluye la retribución a los recursos financieros
del capital invertido, por lo que es bruta, sobre el capital que permanece invertido a principios de cada año.
La rentabilidad relativa neta será la diferencia entre la rentabilidad relativa bruta y el coste de los recursos
que financian al capital inicial -k-.
Como consecuencia de lo anterior, el criterio del TIR no es válido para la comparación de proyectos de
inversión independientes en cuanto a rentabilidad y mutuamente excluyentes, si estos tienen diferentes
duraciones. Por lo que respecta al capital invertido de los proyectos, en principio, no importaría que fuesen
distintos, por cuanto que la TIR proporciona una rentabilidad sobre el volumen de inversión que permanece
invertido.
2.13 ANALOGIAS Y DIFERENCIAS ENTRE LOS CRITERIOS VAN Y TIR
Cuando las inversiones son simples los criterios VAN y TIR determinan la misma decisión con respecto a la
aceptación o rechazo de una inversión.
Consideremos una inversión que genera flujos netos de caja Q1;Q2;...Qn al final de los años 1,2,..n
respectivamente. Como se trata de una inversión simple Q0<0 y Qt>0 (t=1,2,...n).
El método VAN afirma que un proyecto debe aceptarse únicamente si su VAN es positivo. Definimos la
expresión del VAN como:
)
t
k+(1
Qt
n
0=t
=VAN 
El criterio TIR afirma que debe aceptarse un proyecto únicamente si la TIR del proyecto supera el coste de
capital, definimos la TIR como:
)
t
r+(1
Qt
n
0=t
=0 
Si restamos las dos expresiones anteriores, tenemos:









)
t
r+(1
Qt
-
)
t
k+(1
Qt
n
0=t
=VAN

31. 13
Si consideramos un término -t- del segundo miembro de la ecuación anterior:








)
t
r+(1
Qt
-
)
t
k+(1
Qt
para t = 1,2,….n
Como Qt, k y r son todos positivos, la expresión anterior y por lo tanto el VAN es positivo si r>k, cero si r=k, y
negativo si r<k. En este caso, existe equivalencia entre los criterios VAN y TIR para las decisiones de
aceptación y rechazo de una inversión simple.
Si representamos gráficamente la evolución del VAN de un proyecto simple de inversión, éste es función del
coste inicial Q0, de los flujos netos de caja Qi, y de la tasa de actualización. Es decir: VAN = f(Q0,Qi,k)
Si suponemos constantes Q0 y Qi el VAN será una función decreciente y convexa respecto al origen de la tasa k
de actualización, alcanza su mayor valor cuando la tasa de actualización es nula, vale cero cuando corta al eje
de abcisas y tiende a alcanzar un valor próximo a Q0 para tasas de actualización suficientemente altas. Si
efectuamos un análisis de la ecuación que representa el VAN y observamos su evolución en función del coste,
obtenemos las características relevantes descritas anteriormente, así, cuando:
k=0, entonces VAN Q Qtt
n
( )0 0 1
  


0Q)VAN(entonces,k 
edecrecientFuncion0
dk
dVAN(k)

origenalrespectoconvexaFuncion0
k
2
d
VAN(k)
2
d

Trasladando estos datos a un eje cartesiano y representando en el eje de ordenada al VAN del proyecto y en el
eje de abcisas diferentes valores de k, desde cero hasta infinito, tenemos:
VAN
 tQQ0
VAN>0 r<k
r>k r=k VAN<0
- Q0
El tanto de rendimiento interno r será el valor de k que hace igual a cero el VAN. Para costes de capital k
inferiores a r el VAN es positivo y para costes de capital k superiores a r el VAN es negativo.
Del análisis anterior, se desprende que los criterios del valor actual neto y de la tasa interna de rendimiento
conducen a la misma decisión en cuanto a la aceptación o rechazo de un proyecto de inversión simple. Es
decir:
Cuando VAN > 0, también r > k
Cuando VAN = 0, también r = k
Cuando VAN < 0, también r < k
Se acepta el proyecto
Se rechaza el proyecto
Se rechaza el proyecto
Sin embargo, aún tratándose de inversiones simples los métodos VAN y TIR pueden conducir a resultados
distintos cuando se trata de comparar dos o más proyectos y establecer un orden de preferencia entre ellos.
Esto se presenta cuando se trata de proyectos mutuamente excluyentes, ya que en caso contrario, la
clasificación de inversiones sería irrelevante, escogiéndose todo proyecto que proporcione rentabilidad.

32. 14
La razón por la cual dos o más proyectos pueden resultar mutuamente excluyente desde un punto de vista
intrínsico reside en el destino final que la empresa dará a los proyectos en cuestión. Es decir, si una empresa
con determinadas necesidades se encuentra ante ciertas oportunidades de inversión que de una u otra forma le
hacen conseguir el objetivo que se propone, estas inversiones serán mutuamente excluyentes por cuanto que al
satisfacer el mismo objetivo, la realización de una impide la de cualquier otra.
Otra posibilidad para que varios proyectos se conviertan en mutuamente excluyente reside en la existencia de
una restricción externa a los mismos, tal como podría ser una limitación rígida de recursos financieros. Esta
limitación implica una política menos que óptima al conducir al rechazo de inversiones rentables.
Cuando tratamos de comparar dos o más proyectos y establecer un orden de preferencia entre ellos, nos
podemos encontrar con situaciones y problemáticas diferentes en función de las características financieras de
los proyectos que se comparen:
a) Proyectos con iguales desembolsos iniciales e idénticas duraciones temporales.
b) Proyectos con iguales desembolsos iniciales pero distintas duraciones temporales.
c) Proyectos con iguales duraciones temporales pero con diferentes desembolsos iniciales.
d) Proyectos con diferentes desembolsos iniciales y distintas duraciones.
En el primer caso estamos ante lo que se denomina inversiones homogéneas y en los tres restantes, ante la
comparación de inversiones no homogéneas.
Los criterios VAN y TIR aunque ambos evalúan la rentabilidad, cada uno de ellos la expresa y mide de forma
diferente. La TIR proporciona la rentabilidad relativa sobre el capital invertido, mientras se mantenga invertido,
por eso, este criterio sólo exige una igualdad en las duraciones previstas si se desea que los resultados
obtenidos sean consistentes ante la comparación a realizar.
En cambio el criterio VAN mide la rentabilidad absoluta, por eso, exige para que sea consistente que ambos
proyectos tengan igual coste inicial e igual duración prevista.
Para poder comparar proyectos de inversión simples y mutuamente excluyentes dividiremos el análisis en dos
partes, en función de sí los proyectos que se ordenan son homogéneos o no.
Un conjunto de proyectos de inversión se denominan homogéneos cuando todos tienen el mismo desembolso
inicial e idéntica duración temporal. Supongamos dos inversiones mutuamente excluyentes como aparecen en
la figura, puede ocurrir que, en la práctica, las curvas A y B del gráfico no se corten, al menos en el primer
cuadrante, con lo cual, los resultados obtenidos siguiendo cualquiera de los dos criterios coincidirán.
VAN
VANA(0)
VANB(0)
rB rA k
Puede ocurrir que, en la práctica, las curvas A y B del gráfico anterior se corten, al menos en el primer
cuadrante, como ocurre en la figura.

33. 15
VANA(0)
VANB(0)
r*
rA rB k
donde rA y rB son las tasa de rendimiento interno de A y B. La inversión A será preferida según el criterio del
VAN y la B en el caso de que el criterio empleado fuese el TIR.
Sin embargo, cuando el tipo k de actualización es inferior a r
*
según el criterio del VAN es mejor la inversión A
que la B, por corresponderle un VAN mayor. Cuando el tipo k de actualización es mayor que r
*
, ambos criterios
el VAN y la TIR conducen al mismo resultado, es decir, elegir el proyecto B. Puede observarse, pues, que los
resultados obtenidos con uno y otro criterio pueden no coincidir.
Para resolver esta contradicción se busca una tasa de actualización que convierte a las dos inversiones en
equivalentes. Esa tasa de actualización sería el punto de corte entre los proyectos A y B y se llama tasa de
retorno sobre el coste de Fisher, que se corresponde con r
*
en la figura. En el punto de corte tenemos que:
VANA(r
*
)=VANB(r
*
) y rA=rB=r
*
.
2.13.1 Tasa de retorno sobre el coste de Fisher
Analíticamente la podemos definir como aquella tasa de actualización o descuento que iguala los valores
actuales netos de dos proyectos de inversión.
n
)
*
r(1
nQ
......
)
*
r(1
1Q
0Q
n
)
*
r(1
nQ
.......
)
*
r(1
1Q
0Q










Agrupando términos y operando, tenemos:




n
1t
0
n
)
*
r(1
tQtQ
Desde un punto de vista económico, el conocimiento de la tasa de Fisher proporciona a la empresa una
información referente a la tasa de descuento o coste de capital, a partir del cual los criterios del VAN y de la TIR
llegarán a la misma decisión de ordenación jerárquica.
La posible disparidad en los resultados que se obtienen al aplicar uno u otro criterio, cuando se trata de ordenar
una lista de proyectos de inversión, se debe, como ya hemos visto a que ambos criterios se apoyan en
supuestos diferentes y miden cosas distintas.
Ahora bien, teniendo en cuenta:
1º. - El supuesto implícito del criterio TIR, de que los proyectos de inversión tienen un coste de oportunidad igual
a la TIR del proyecto, sin tener en cuenta el coste de oportunidad determinado por el mercado que resulte
apropiado según su riesgo.
2º. - Que el criterio TIR no obedece al principio de aditividad del valor.
3º. - La existencia de tasas múltiples de rendimiento siempre que el signo de los flujos de caja cambie más de
una vez.
La utilización del criterio del VAN ofrece una conexión directa con el objetivo general de la empresa que es la
maximización del valor de mercado de las acciones.

34. 16
VALORACION Y SELECCIÓN DE PROYECTOS DE INVERSION. II
2.14 LA ORDENACIÓN DE PROYECTOS NO HOMOGÉNEOS
Dos o más proyectos de inversión se consideran no homogéneos cuando tienen diferentes duraciones
temporales y/o distintos desembolsos iniciales. Para ordenar proyectos de inversión simples, excluyentes, no
repetitivos y no homogéneos tendremos que homogeneizar las duraciones y los desembolsos iniciales.
2.15 COMPARACIÓN DE PROYECTOS CON DIFERENTES DURACIONES
Podemos encontrarnos con los siguientes supuestos:
2.15.1.- Proyectos con igual coste e igual VAN pero con diferente duración
Cuando nos encontramos ante dos proyectos de inversión con iguales costes iniciales Q0 = Q'
0 e igual valor
actual neto VAN = VAN'
, siendo las duraciones respectivas n y n'
(n>n'
), el inversor se inclinará por el proyecto
de menor duración (a pesar de que ambas tienen iguales VAN) debido a que da lugar a una misma
rentabilidad absoluta para una misma inmovilización monetaria, en menor tiempo.
Por tanto, al objeto de llegar a resultados coherentes, deberemos homogeneizar las duraciones previstas de
los proyectos a comparar. Para ello, tenemos dos alternativas:
Supongamos estos dos proyectos de inversión A y B, simples, no repetitivos y mutuamente
excluyentes:
Inversión CF0 CF1 CF2 CF3 CF4 k VAN
A 8.525,6 2.055,87 2.995,84 3.105,53 2.014,78 6% 283,63
B 8.525,6 4.352,06 5.284,87 6% 283,63
1. - Considerar un horizonte temporal igual a la menor de las duraciones de los proyectos propuestos, lo cual
exige conocer, del proyecto de mayor duración los siguientes datos:
a) Su valor residual en el instante que finaliza el de menor duración. Este valor se sumará al flujo neto de caja
de aquel momento, consiguiéndose así la homogeneización deseada.
b) La tasa de actualización de los flujos netos de caja obtenidos con posterioridad a la terminación del proyecto
de menor duración. Con este dato, actualizaremos dichos flujos al instante de finalizar el proyecto más corto.
Para igualar las duraciones recurrimos al concepto de reinversión de los flujos intermedios de caja para
aquellos flujos que se obtienen con anterioridad al vencimiento de la inversión más corta (flujos de los
años 1 y 2). Recurrimos al concepto de actualización de los flujos de caja de la inversión más larga al
periodo final de la inversión más corta. Como la inversión más corta (B) termina en el año 2, actualizamos al
año 2 los flujos de caja de los años 3 y 4 de la inversión A. Si la tasa de reinversión coincide con el coste de
capital el VAN sigue siendo el mismos para las dos inversiones, para tr < k, IA > IB, en cambio, para tr > k la
IB > IA, como en el ejemplo siguiente para tr = 4%
En este caso sigue interesando la inversión A.
17.206
)06.1(
87.5284)04.1(06,4352
6,525.8
95,246
)06.1(
)06.1(
78,2014
)06.1(
53,3105
84,2995)04.1(87,2055
6,525.8
2
2
2






B
A
I
I

35. 17
2. - Suponer un horizonte temporal igual a la duración mayor de los diferentes proyectos a comparar. Para
este método deberá ser conocida la tasa de reinversión de los flujos netos de caja del proyecto más corto,
desde la terminación de su horizonte temporal hasta el correspondiente al proyecto más largo.
Para igualar las duraciones recurrimos al concepto de reinversión de los flujos intermedios de caja al tipo de
interés existente en el mercado y teniendo como duración, la duración de la inversión más larga:.
Si la tasa de reinversión coincide con el coste de capital el VAN sigue siendo el mismo para las dos
inversiones, para tr < k, IA > IB, en cambio, para tr > k la IB > IA, como en el ejemplo siguiente para tr = 8%::
( ) ( ) ( )
( )
( ) ( )
( )
En este caso interesa la inversión B
3.- En el supuesto de que las inversiones fueran simples, repetitivas y excluyentes tendríamos que
igualar las duraciones repitiendo los proyectos de inversión, y suponemos de idénticos flujos de caja (equipo
de iguales características y se mantienen constantes las condiciones en que se realiza el proyecto).
Podemos renovar dos veces la inversión A y cuatro veces la inversión B, en este supuesto es preferible la
inversión B a la inversión A (en los flujos netos de caja de la inversión B de los años 2, 4 y 6 hemos incluido
el coste inicial de la renovación).
En este supuesto sigue interesando la inversión B.
2.15.2.- Proyectos con distinto coste, distinto VAN y diferente duración.
Tenemos los siguientes proyectos de inversión con un coste de capital del 5%:
2.15.2.1.- Que sean proyectos no repetitivos
El VAN del proyecto A es mayor que el VAN del proyecto B, pero el proyecto B se recupera más pronto que
el A, si ambos proyectos no están relacionados con la actividad principal de la empresa, es decir no se
pueden repetir a la hora de tomar una decisión podemos utilizar el método del “Flujo anual equivalente al
VAN (FAE)” que consiste en calcular el excedente anual de la inversión (equivalente a cobrar una renta
anual), mediante la fórmula:
VAN = FAEani  FAE = VAN/ani
Flujo anual equivalente al VAN de los proyectos:
VAN DURACION EQUIV. ANUAL
A 3.075,69 6 605,97
B 2.557,20 3 939,02
Aplicando este método la conclusión es distinta de la aplicación del VAN, es mejor la inversión B ya que el
excedente es mayor.
Al ser distinta la duración hay que pensar qué hacer con el excedente de la inversión B, si es no repetitiva
tendremos que buscar una inversión alternativa durante los tres últimos años y lo más prudente será
INV / PERIODO Inicial 1 2 3 4 5 6 7 8 VAN
A -8.525,60 2.055,87 2.995,84 3.105,53 -6.510,82 2.055,87 2.995,84 3.105,53 2.014,78 508,14
B -8.525,60 4.352,06 -3.240,73 4.352,06 -3.240,73 4.352,06 -3.240,73 4.352,06 5.284,87 960,68
INV / PERIODO Inicial 1 2 3 4 5 6 VAN
A -2.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 3.075,69
B -1.800,00 1.600,00 1.600,00 1.600,00 2.557,20

36. 18
considerar inversiones que tengan un VAN = 0 (se reinvierte el excedente a una tasa tr = k, de esta forma no
se generan más excedentes). En el año 3 reinvertimos el valor final para recuperarlo el sexto año
capitalizado al 5% durante tres años.
.
en este caso los FAE sería:
VAN DURACION EQUIV. ANUAL
A 3.075,69 6 605,97
B 2.557,20 6 503,81
Como conclusión al igualar las dos duraciones como consecuencia de incluir al inversión alternativa, tanto
por el método FAE como por el método VAN el mejor proyecto es A.
2.15.2.2.- Que sean proyectos repetitivos
Son proyectos que están relacionados con la actividad de la empresa, por tanto, cuando finalice el proyecto
más corto habrá que iniciar un nuevo proyecto (inversiones repetitivas) de igual duración y suponemos de
idénticos flujos de caja (equipo de iguales características y se mantienen constantes las condiciones en que
se realiza el proyecto), en este caso el proyecto más corto igualaría en duración al proyecto más largo.
En el proyecto B que vamos a repetir, en el flujo de caja del año 3 vamos a incluir el coste inicial de la
renovación, por tanto, el flujo será: +1.600 – 1800 = -200.
El VAN de los dos proyectos será ahora:
INV / PERIODO Inicial 1 2 3 4 5 6 VAN
A -2.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 3.075,69
B -1.800,00 1.600,00 1.600,00 -200,00 1.600,00 1.600,00 1.600,00 4.766,20
El proyecto B tiene un VAN mayor que A y, un mayor flujo anual equivalente, es por tanto más deseable (el
inconveniente es suponer una estabilidad en los precios en la próxima renovación).
Flujo anual equivalente al VAN de los proyectos
VAN DURACION EQUIV. ANUAL
A 3.075,69 6 605,97
B 4.766,20 6 939,02
En este supuesto tanto por el VAN con renovación como por los FAE es mejor el proyecto B.
2.15.2.3 Que los proyectos se puedan renovar indefinidamente
Bajo el supuesto de estabilidad de precios, si los proyectos se pudieran renovar indefinidamente la
expresión del VAN de la cadena ilimitada de renovaciones sería (siendo –n- el número de años del proyecto
y –m- el número de renovaciones, para –m- tendiendo a infinito) :
VANGlobal = VAN1 + VAN2 + …………………………… + VANm
Siendo: VAN1 = el VAN original; VAN2 = VAN1/(1+k)n
; VAN3 = VAN1/(1+k)2n
………..VANm = VAN1/(1+k)nm
VANGlobal = VAN1((1+k)
n
/(1+k)
n
-1))
VANG(B) = 2.557,20*((1.05)3
/((1.05)3
-1)) = 18.780,51
VANG(A) = 3.075,69*((1.05)
6
/((1.05)
6
-1)) = 12.119,29
En el supuesto de renovación ilimitada, sigue siendo preferible el proyecto B.
INV / PERIODO Inicial 1 2 3 4 5 6 VAN
A -2.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 3.075,69
B -1.800,00 1.600,00 1.600,00 -1.360,28 0,00 0,00 3.426,89 2.557,19

37. 19
2.16 OTROS MÉTODOS DE SELECCIÓN
En el apartado anterior las duraciones de los proyectos eran múltiplos, pero en la práctica cuando no se da
esa coincidencia hay que encontrar el mínimo común múltiplo de las duraciones de todos los proyectos.
Para evitar este procedimiento que podría llevar a duraciones absurdas podemos utilizar el método del
Valor Actual de los Pagos (VAP).
Este método lo podemos utilizar a la hora de comparar inversiones relacionadas con la actividad de la
empresa (maquinaria), los distintos proyectos tendrán algo en común que serían los ingresos (si el objetivo
es atender una demanda creciente), lo que diferencia a los distintos proyectos serán los costes de
mantenimiento y los consumos. Partiendo de la expresión del flujo de caja como diferencia entre los cobros
y pagos podemos obtener la siguiente expresión:
FCj = Cobrosj - Pagosj su valor actual será igual: VA(FCj) = (Cj – Pj)/(1+k)
j
en la expresión del VAN podemos sustituir el valor actual de los flujos de caja por sus componentes, la
expresión sería:
VAN = - CFo + (C1 -P1 )/(1+k) + (C2 -P2 )/(1+k)2
+ …. = - CFo + C1 /(1+k) – P1 /(1+k) + C2 /(1+k)2
– P2
/(1+k)2
+ …….. = (+C1 /(1+k) + C2/(1+k)2
+ ….) – (CFo + P1 /(1+k) + P2 /(1+k)2
+ ….)
De esta forma, la expresión del VAN quedaría: VAN = VA(Cobros) – VA(Pagos)
Como VA de los Cobros será similar entre los distintos proyectos, elegiremos aquellos proyectos que tengan
un menor VA de los Pagos, de esta forma indirecta obtenemos el mejor VAN.
Siguiendo con el ejemplo, si suponemos unos ingresos iguales para los dos proyectos durante todos los
años de 2.000 euros, los gastos anuales serán de 1.000 euros para el proyecto A y de 400 euros para el
proyecto B, de esta forma, el VAP sería:
Es preferible el proyecto B.
Si hay que repetir la inversión B el VAP quedaría:
Sigue siendo preferible el proyecto B
Si las magnitudes son los costes de los proyectos, podemos calcular el “Coste anual equivalente (CAE)”
que sería la traslación del VAP de los pagos entre los distintos años de vida de los proyectos:
Sigue siendo preferible el proyecto B
2.17 COMPARACIÓN DE PROYECTOS CON DESEMBOLSOS DIFERENTES
Nos podemos encontrar con distintas situaciones:
2.17.1.- Proyectos con distinta inversión e igual duración y VAN
1.- Supongamos tres inversiones independientes con una duración de 6 años y un coste de capital del 10%
INV / PERIODO Inicial 1 2 3 4 5 6 VAN
A 2.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 7.075,69
B 1.800,00 400,00 400,00 400,00 2.889,30
INV / PERIODO Inicial 1 2 3 4 5 6 VAN
A 2.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 1.000,00 7.075,69
B 1.800,00 400,00 400,00 2.200,00 400,00 400,00 400,00 5.385,18
VAN DURACION EQUIV. ANUAL
A 7.075,69 6 1394,03
B 5.385,18 6 1060,98

38. 20
INV "A" INV "B" INV "C"
VA Flujos de cobros 25.360 50.450 15.800
VA Flujos de pago (inversión) 20.200 45.290 10.640
VAN 5.160 5.160 5.160
Flujo Anual equivalente al VAN - FAE 1.184,77 1.184,77 1.184,77
Valor actual relativo VAR 1,26 1,11 1,48
Indice de Rentabilidad 20,35% 10,23% 32,66%
FAE / Coste inversión 5,87% 2,62% 11,14%
Las tres inversiones tienen el mismo VAN y por tanto el mismo FAE. El orden de preferencia es C – A – B. Esta
ordenación que la realizamos de forma intuitiva la podemos validar con la expresión del VAR (Valor actual
relativo) que consiste en dividir el VA de los ingresos entre el VA de los pagos (incluida la inversión),
Para la inversión C por cada euro de inversión se generan 1.48 euros de ingresos. También lo podemos validar
con el IR, la inversión C obtiene una rentabilidad del 32.66% y, por último, dividiendo el flujo anual equivalente
del VAN por la inversión, sigue siendo la inversión C con el 11.14% la mejor inversión.
Cuando los proyectos son independientes y tienen la misma duración y el mismo VAN, la decisión es elegir
aquel proyecto que tiene mayor VAR.
2.- Cuando nos encontramos ante dos proyectos de inversión mutuamente excluyentes de idéntica duración
prevista y supuesto un mismo valor actual neto, pero con costes iniciales Q0 y Q'0 siendo Q0>Q’0', el criterio del
VAN nos dice que es indiferente elegir una u otra. Sin embargo, sabemos que todo inversor preferirá el
proyecto de menor coste inicial, por implicar una inmovilización monetaria más pequeña e idéntica rentabilidad
bruta.
Para poder comparar dos inversiones por el criterio del VAN con distinto coste inicial debemos homogeneizar
los costes iniciales con ayuda de la inversión diferencial o complementaria (una vez que tengamos ya
homogeneizadas las duraciones). Esta se define por la inversión diferencia Id entre los costes iniciales (Q0-Q
'
0)
en el supuesto de ser Q0>Q
'
0 y viceversa, durante el horizonte temporal común a los proyectos tratados, a una
tasa conveniente (dada por las oportunidades a las que puede acceder la empresa considerada). Llamando tr a
la tasa de inversión de la diferencia entre los costes iniciales, la comparación se realizará entre los valores
actuales netos de la inversión de mayor coste inicial Q0 y de la inversión suma de la de menor coste inicial Q
'
0
con la diferencia Id. Los recursos no utilizados del proyecto de inversión de menor coste se emplearán en
inversiones que tengan un VAN = 0 (se reinvierte el excedente a una tasa tr = k, de esta forma no se
generan más excedentes).
Tenemos los siguientes proyectos de inversión X e Y, simples y mutuamente excluyentes:
Inversión CF0 CF1 CF2 k VAN
X 5.250,7 2.123,5 4.150,6 6% 446,62
Y 8.216,25 4.323,4 5.150,8 6% 446,62
Las dos inversiones tienen el mismo VAN luego, es indiferente elegir entre X e Y, pero en la práctica,
elegiremos la inversión X ya que representa una menor inmovilización monetaria. Para realizar alguna de
las dos inversiones la empresa debe contar con unos recursos equivalentes a 8.216,25 €.
En este caso para poder comparar las dos inversiones tendremos que igualar los desembolsos iniciales:
Si la empresa elige la inversión X, al ser su coste de 5.250,7 € le sobran 2.965,56 € (8.216,25 – 5.250,7 =
2.965,55). Con ese dinero la empresa debe realizar una inversión Id, estando remunerada a una tasa tr = k,
a un plazo igual a la duración de la inversión.
En este ejemplo sería: Id = 2.965,55; tr = 6% y t = 2 años. Transcurridos dos años tendríamos:
2.965,55(1+0.06)2
= 3.332,10

39. 21
De esta forma, elegir la inversión X implica realizar también la Id. Tenemos ahora una nueva inversión
formada por la inversión (X + inversión Id ) siendo su desembolso inicial comparable con la inversión Y.
Inversión CF0 CF1 CF2 k VAN
X 5.250,7 2.123,5 4.150,6 6% 446,62
Id 2.965,55 3.332,10 6% 0,00
X+Id 8.216,25 2.123,5 7.482.70 6% 446.62
Y 8.216,25 4.323,4 5.150,8 6% 446,62
Para tr = k la decisión seguiría siendo elegir la inversión X (menor coste inicial), para tr < k la decisión sería
elegir la inversión Y, para tr > k la decisión sería elegir la inversión X.
¿Cambiaría la decisión si el criterio de decisión empleado fuera el VAR?. En las dos tablas siguientes
tenemos el VAR de los dos proyectos de inversión. El proyecto X más la Id y el proyecto Y.
El VAR es el mismo para los dos proyectos, la decisión seguirá siendo elegir el proyecto X.
2.18 REEMPLAZO DE EQUIPOS INMOVILIZADOS
Son equipos que están en funcionamiento y se plantea la posibilidad de cambiarlo por motivos tecnológicos
por equipos más modernos y eficientes con menores costes. Para analizar una inversión de remplazo,
podemos seguir los siguientes pasos:
- El valor residual del equipo viejo disminuye el coste del nuevo.
- Hay que calcular si se producen plusvalías/minusvalías en la venta del equipos viejo, ya que hay
que tener en cuenta el efecto fiscal.
- Se trabaja con los flujos de caja incrementales, teniendo en cuenta los ahorros de costes que
producen los equipos nuevos pero también, la deducción fiscal de los gastos del equipo viejo que se
ha vendido.
EJEMPLO: Una empresa está estudiando cambiar un equipo por otro más moderno que funcionará con tres
operarios menos. Esto implicará un ahorro en salarios de 440.000 € anuales. La nueva máquina costará
2.500.000 de € tendrá una vida útil de 10 años al final de los cuales se podrá vender por 400.000 €.
La máquina vieja costó 1.500.000 de € hace 5 años y puede funcionar todavía durante 10 años más. Si decide
venderla su valor en el mercado de segunda mano es de 600.000 €.
Los costes de mantenimiento de la nueva máquina son los mismos que los de la vieja. La tasa impositiva sobre
beneficios es del 30% y el coste de capital para la empresa es del 12%. ¿Se debe sustituir la máquina vieja por
la nueva?.
Año 5 Flujos de Caja incrementales 6 a 15
Coste equipo nuevo 2.500.000 Ahorro salarios 440.000
Valor contable equipo viejo 1.000.000 Amortización equipo nuevo -210.000
Coste 1.500.000 Pérdida amort equipo viejo 100.000
Amortización Acumulada 500.000 FC incremental 330.000
Venta equipo viejo 600.000 Cuota 30% 99.000
Pérdida venta -400.000 FCDI 231.000
Ahorro impositivo -120.000 Amortización 110.000
Total Pago -1.780.000 Total cobro 341.000
En el último año habría que añadir en el flujo de caja el valor residual de la máquina nueva por 400.000
INV "X" INV "Id" INV "X + Id" INV "Y" INV "Id" INV "Y + Id"
VA Flujos de cobros 8.170,23 2.965,55 11.135,78 VA Flujos de cobros 10.688,68 0,00 10.688,68
VA Flujos de pago (inversión) 7.723,78 2.965,55 10.689,33 VA Flujos de pago (inversión) 10.242,06 0,00 10.242,06
VAN 446,45 0,00 446,45 VAN 446,62 0,00 446,62
Flujo Anual equivalente al VAN 243,60 0,00 243,60 Flujo Anual equivalente al VAN 243,60 0,00 243,60
Valor actual relativo VAR 1,06 1,00 1,04 Valor actual relativo VAR 1,04 1,04

40. 22
Al ser el VAN incremental positivo podemos realizar la renovación.
Otra forma de estudiar la conveniencia de realizar el remplazo de un equipo es comparando los costes de
mantenimiento del equipo nuevo con los costes de mantenimiento del viejo, teniendo en cuenta el valor
residual del viejo en cada uno de los años que le quedan de vida, considerando el coste de oportunidad en
el que incurre cada año por no vender el equipo viejo. Este coste de oportunidad es el resultado de
multiplicar el VR del equipo que no se ha vendido en el año por el coste de capital que sería la rentabilidad
que deja de ganar en ese año.
EJEMPLO: En la actualidad tenemos un equipo que le queda 5 años de vida útil, con los siguientes costes
de mantenimiento y valor residual para dichos años:
Se podría sustituir por un equipo nuevo con un coste de 100.000 y una vida útil de 8 años, siendo su valor
residual de 5.000. Los costes de mantenimiento del equipo son de 20.000 anuales. El coste de capital para
la empresa es del 5%.
Como tenemos los costes de los dos equipos, podemos trabajar con el Valor actual de los Pagos (VAP) y
también con el Coste anual equivalente (CAE).
1.- Valor actual de los pagos del equipo nuevo y su CAE:
Flujo anual equivalente al Pago de los proyectos:
VAP DURACION EQUIV. ANUAL
A 225.880,06 8 34.948,57
El CAE del equipo nuevo de 34.948,57 es constante durante los 8 años de vida del proyecto. Lo tenemos
que comparar con el CAE anual de mantener el equipo viejo.
2.- Valor actual de los pagos y CAE del equipo viejo:
Año
Coste
mantenimiento V.Residual
Coste
oportunidad Coste total año VAP CAE
0 40.000
1 30.000 35.000 42.000 37.000 35.238,10 37.000,00
2 20.000 25.000 36.750 31.750 64.036,28 34.439,02
3 20.000 15.000 26.250 31.250 91.031,21 33.427,44
4 30.000 10.000 15.750 35.750 120.442,82 33.966,30
5 40.000 5.000 10.500 45.500 156.093,26 36.053,61
El CAE del equipo viejo disminuye los primeros años para volver a subir, el CAE del equipo nuevo se
mantiene constante en 34.948,57, si representamos gráficamente los dos CAE no haremos una idea de cuál
es el mejor momento para su renovación.
Inicial 1 2 3 4 5 6 7 8 9 10 VAN
-1.780 341 341 341 341 341 341 341 341 341 741 275,52
INV /PERIODO Inicial 1 2 3 4 5 6 7 8 VAN
A 100.000,00 20.000,00 20.000,00 20.000,00 20.000,00 20.000,00 20.000,00 20.000,00 15.000,00 225.880,06
Año Coste mantenimiento Valor Residual
0 40.000
1 30.000 35.000
2 20.000 25.000
3 20.000 15.000
4 30.000 10.000
5 40.000 5.000

41. 23
Interesa mantener el equipo hasta el año 4 y cambiarlo en ese momento.
2.19 RACIONAMIENTO DE CAPITAL
Cuando existe racionamiento de capital no se pueden realizar todas las inversiones con VAN positivo ya
que existe una limitación de recursos, Cuando las inversiones son excluyentes hay que elegir aquella que
proporcione un mayor VAN. Cuando las inversiones son independientes hay que elegir aquella combinación
de inversiones con mayor VAN hasta agotar el presupuesto de capital.
2.20 DISTRIBUCION TEMPORAL ÓPTIMA DE LAS INVERSIONES
Cuando el VAN de una inversión es mayor que cero la decisión siempre ha sido realizar la inversión. Esta
inversión se realizaba en el momento t = 0, sin analizar si el proyecto tendría más valor de realizarse en un
futuro: t = 1, t = 2,…. La decisión sería invertir ahora o invertir más tarde, son dos decisiones mutuamente
excluyentes, son inversiones que se esperan que en un futuro los flujos netos de caja sean mayores siendo
también mayor la inversión necesaria. Cuando los flujos netos de caja no son ciertos, tomar una decisión
sobre el momento óptimo de realizar la inversión implica trabajar con el valor actual neto esperado y su
correspondiente tasa de variabilidad, circunstancias que complican la toma de decisiones.
En primer lugar, la empresa debe identificar los períodos adecuados en que puede realizar la inversión,
seguidamente realizar la previsión de los distintos flujos netos de caja y el VAN de cada uno de los
períodos. Como los VAN obtenidos corresponden a distintos momentos de tiempo para poder tomar una
decisión hay que actualizarlos al momento inicial y elegir aquél período que presente un mayor VAN
actualizado.
31.000,00
32.000,00
33.000,00
34.000,00
35.000,00
36.000,00
37.000,00
38.000,00
1 2 3 4 5
CAE VIEJO CAE NUEVO

42. 24
SELECCIÓN DE INVERSIONES EN REGIMEN DE INCERTIDUMBRE
2.21 INTRODUCCION
Cuando una empresa debe tomar una decisión, los resultados dependen de un conjunto de factores no
controlados, que se suelen denominar estados de la naturaleza. Estas decisiones se toman esperando
obtener de ellas unas determinadas y deseables consecuencias. Pero la consecuencia de toda decisión
cuyos resultados se producirán en el futuro suele ser, por naturaleza, incierta, y tomar la decisión equivale a
hacer una apuesta sobre lo que ha de acontecer.
El objetivo financiero de la empresa es maximizar el valor de mercado de las acciones, por eso en ambiente
de certeza equivale a elegir aquellas inversiones que tienen mayor VAN. En ausencia de certeza, cuando
haya que elegir entre distintas inversiones, elegiremos aquélla en la que el resultado más probable es el
mejor, rechazando aquellas en las que lo más probable es que se produzca un resultado menos bueno. Sin
embargo, al hacer esta elección, se corre el riesgo de que suceda lo improbable o, que ocurra un suceso de
menor probabilidad, ocasionando un resultado no deseado. Ello no significaría que la decisión no hubiera
sido correcta, significaría que se habría materializado el riesgo incurrido al tomarla.
Cuando no se conocen las probabilidades de ocurrencia de los distintos estados de la naturaleza se dice
que estamos en un ambiente de incertidumbre, cuando se conocen las probabilidades de ocurrencia de
los distintos estados de la naturaleza se dice que estamos en un ambiente aleatorio. Una situación de total
incertidumbre es tan irreal como una situación con información perfecta. Una situación de total incertidumbre
se pude transformar en aleatoria asignando probabilidades subjetivas a los distintos estados de la
naturaleza. En este supuesto, el proceso de formación de los criterios de decisión es muy complejo por el
peso que en él tienen los factores psicológicos personales, especialmente la aversión o la inclinación al
riesgo.
En una situación incierta, el decisor a la hora de tomar una decisión, tendrá que tener en cuenta además de
las técnicas de análisis y selección de proyectos, las técnicas aportadas por la teoría de probabilidades, y
por la función de utilidad del propio decisor.
En este tema veremos distintos métodos para tratar la incertidumbre, así como, el método del valor actual
de los flujos netos de caja al coste de capital, pero teniendo en cuenta, por un lado las probabilidades
atribuibles a los distintos valores que, a lo largo del horizonte de vida del proyecto, pueden tomar tanto los
flujos de caja inherentes al proyecto como el coste de capital, y, por otro lado, el valor subjetivo, es decir, el
valor que para el decisor tendrá el resultado que, en términos objetivos, puede producir el proyecto, sobre
todo, en el caso de que se materialice alguna de las posibilidades adversas.
2.22 TRATAMIENTO DEL RIESGO
A.- Tratamiento implícito del riesgo:
- Coste de capital medio ponderado: en aquellos proyectos de inversión con iguales características y niveles
de riesgo a los de la empresa que los evalúa.
B.- Tratamiento explícito del riesgo:
1. - Métodos aproximados: Consideran el riesgo explícitamente, midiéndolo de forma subjetiva e
incorporándolo a la cuantificación de la rentabilidad, a la cual corrigen en función del nivel de riesgo del
proyecto.
- El ajuste de la tasa de descuento mediante una prima por riesgo.
- La reducción a condiciones de certeza de los flujos netos de caja del proyecto a evaluar.
- Análisis de la sensibilidad.

43. 25
2. - Métodos estadísticos: Consideran el riesgo explícitamente mediante una medida del mismo que
generalmente se expresa por la varianza de la rentabilidad. La medida del riesgo puede realizarse a través
de datos objetivos o subjetivos, estando estos últimos basados en la denominada probabilidad subjetiva.
Esta probabilidad subjetiva se puede objetivizar con ayuda de Bayes.
- Análisis de las decisiones secuenciales (árboles de decisión).
- El modelo de Hillier.
- Simulación estadística. El modelo de Hertz.
Una vez obtenidos los resultados por medios estadísticos, a la hora de establecer una norma de decisión
debemos ayudarnos del concepto de eficiencia, entendiendo por tal, y en referencia a una inversión, aquella
que a igualdad de rentabilidad proporciona mínimo riesgo, y además aquella que para su nivel de riesgo
proporciona la máxima rentabilidad. Para ello representaremos en un eje rendimiento-riesgo todas las
oportunidades de inversión de una empresa. Del conjunto de oportunidades de inversión, elegiremos
aquella inversión eficiente que sea la adecuada a las preferencias del decisor en cuanto a rentabilidad y
riesgo, es decir teniendo en cuenta su función de utilidad.
3. - El Capital Asset Pricing Model, C.A.P.M.: Generaliza para cualquier situación la medida y tratamiento del
riesgo. Utiliza la metodología procedente de la teoría de carteras, la cual está basada en el concepto de
diversificación, para conseguir de esta forma, la reducción del riesgo empresarial.
2.23 AJUSTE DE LA TASA DE DESCUENTO
Es una de las formas más sencillas de introducir el riesgo en los modelos clásicos de selección de inversiones.
Hasta ahora hemos considerado que todas las magnitudes que definían un proyecto de inversión se
consideraban conocidas y que, la empresa, utilizaba como tasa de actualización, una tasa que coincidía con su
coste de capital. Ahora, al tratarse de proyectos con riesgo, la tasa de descuento habrá que incrementarla
convenientemente en función del riesgo de la inversión. La nueva tasa de descuento ajustada al riesgo será:
s = k + p: Donde k es la tasa de descuento de un activo sin riesgo y p la prima por riesgo. Para el cálculo del
VAN utilizamos la siguiente expresión::
s)+(1
)QE(
+)Q-E(=VAN j
j
n
1j=
0 
Donde los distintos flujos netos de caja son los valores estimados, la decisión será elegir aquel proyecto de
inversión cuyo valor esperado del VAN sea el mayor. La dificultad de este método consiste en determinar la
prima por riesgo p, en que debemos incrementar la tasa de descuento en función del riesgo inbherente al
proyecto. Se trata de algo subjetivo que dependerá de la apreciación personal del inversor y por lo tanto
llevará siempre aparejado un elevado margen de arbitrariedad. Cuando el proyecto tiene el mismo riesgo
que los otros proyectos que tiene en marcha la empresa y su financiación presenta la misma estructura que
su pasivo actual, se utiliza como tasa de actualización ajustada al riesgo su coste de capital medio
ponderado (CCMP).
2.24 EQUIVALENTES DE CERTEZA
Consiste en ajustar en función del riesgo los flujos netos de caja esperados. Supongamos que Q1 es cierto, su
valor actual lo calculamos descontándolo a la tasa de interés libre de riesgo Rf.
Rf+1
Q1
=VA
Si el flujo de caja Q1 fuese arriesgado, su valor actual lo obtendríamos descontando el flujo de caja (previsto) a
una tasa de descuento ajustada al riesgo s que será mayor que Rf. Este procedimiento consiste en determinar

44. 26
¿qué cantidad estaría dispuesto un inversor a recibir con certeza en lugar de una cantidad Q1 con riesgo?. Si
llamamos:
E(Q1 ) = flujo neto de caja con riesgo.
EC1 = cantidad que estaría dispuesto a recibir con certeza en lugar de Q1.
Rf = rentabilidad de un activo sin riesgo.
s = tasa de descuento ajustada al riesgo de Q1.
La cantidad cierta a recibir al final del año 1 será menor que la cantidad a recibir con riesgo. Si para el inversor
es indiferente recibir EC1 que E(Q1) en el año 1, quiere decir que sus valores actuales deben ser los mismos.
Para obtener el valor actual del EC1 utilizamos la tasa de actualización libre de riesgo Rf. Para obtener el valor
actual del flujo neto de caja utilizamos la tasa de actualización ajustada a su riesgo s.
111
f
1
11
f
11
f
1
)xαE(QEC
s)(1
)R(1
)E(Q
EC
s1
)E(Q
R1
EC
s+1
)QE(
VA=
R+1
EC
=VA 







Donde α representa la relación entre el equivalente cierto de un flujo de tesorería y su valor esperado, se
denomina coeficiente de certeza:
( )
Los valores del coeficiente de certeza oscilan en un intervalo comprendido entre 0 y 1, de forma que cuando el
riesgo es nulo el coeficiente toma el valor 1 y cuando el riesgo es muy elevado el coeficiente toma el valor 0.
Conforme los flujos de caja están más alejados en el tiempo el riesgo es mayor por tanto el coeficiente a aplicar
a los flujos de caja es menor, es decir el coeficiente de certeza en decreciente en función del tiempo. Si bien,
existen inversiones donde el riesgo aparece en los primeros años de vida del proyecto, disminuyendo conforme
nos alargamos en el tiempo.
Cuando el equivalente de certeza se aplica a activos duraderos, la expresión sería:
)R+(1
Qα
=
)R+(1
EC=VA
f
j
jj
nj=
1j=f
j
1
nj=
1j=

2.25 ANÁLISIS DE LA SENSIBILIDAD
El análisis de la sensibilidad estudia la influencia de una variación en el valor numérico de alguno o algunos de
los parámetros (pago de la inversión, vida útil, flujos netos de caja, tasa de actualización) sobre las decisiones
de inversión basadas en los criterios VAN y TIR. Para este estudio, suelen elegirse aquellos parámetros cuya
determinación está sujeta a un mayor grado de incertidumbre. Cuando se efectúan estos análisis suele ser muy
útil establecer los valores límites que pueden alcanzar los parámetros que caracterizan el proyecto, compatibles
con la viabilidad de la inversión. En general, podemos establecer los límites máximos para el pago de la
inversión, para los flujos netos de caja y para la tasa de actualización de manera que la inversión sea viable.
Cuando el VAN es positivo, el proyecto es viable. Ahora bien, podemos estar interesados en determinar el valor
máximo que puede tomar el pago de la inversión sin que el proyecto pierda por ello su carácter viable, en el
supuesto de que se mantengan constantes los valores de los demás parámetros. Dicho valor máximo se
obtiene de la siguiente expresión:
)
j
k+(1
Q j
n
1=j
=Q0(max) 
Siempre que el pago de la inversión no supere dicha cantidad, el proyecto será viable.
En cambio, para el resto de flujos de caja hay que obtener el valor mínimo generado en el año p-ésimo,
compatible con la viabilidad del mismo, cuando se mantienen constantes los demás parámetros, será:

45. 27
)
p
k+](1
k)+(1
j
Q j
n
1+p=j
+
k)+(1
j
Q j
1-p
1=j
-Q0
[=Qp(min) 
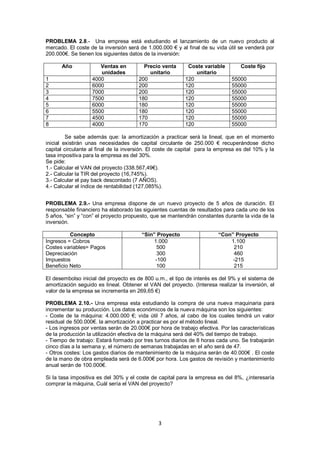
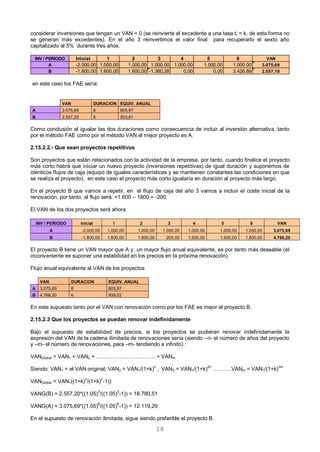
El valor máximo que puede alcanzar la tasa de actualización kmax para que el proyecto sea viable, en la
hipótesis de que los demás parámetros permanezcan constantes, coincidirá con la tasa interna de rendimiento
del proyecto:
0=
)kmax+(1
Q j
n
1=j
+Q0
- 
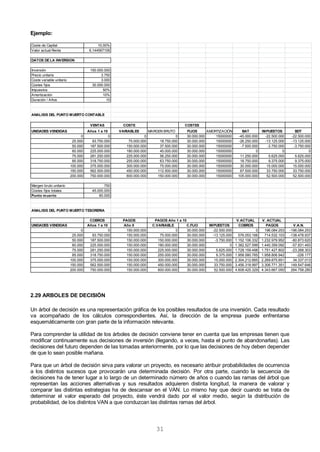
En otras ocasiones, el análisis de sensibilidad se efectúa haciendo variar los precios de los principales inputs y
outputs que intervienen en la inversión y analizando la repercusión que estas variaciones tienen sobre los
distintos criterios de selección de inversiones. Los pasos a seguir en este análisis son los siguientes:
1.- Se calculan los valores previstos de las distintas variables, con dichos valores se calcula el VAN esperado
utilizando una tasa de actualización ajustada al riesgo.
2.- Para cada una de las variables se calculan unos valores pesimistas y otros optimistas. A continuación se
calcula el VAN para cada estimación pesimista y optimista de cada una de las variables manteniendo las otras
variables con sus valores previstos en el punto 1). De esta forma vamos obteniendo la sensibilidad del VAN
ante el cambio de cada una de las variables en su estimación optimista y pesimistas, de esta forma, obtenemos
qué variables contribuyen a mejorar el VAN o por el contrario, qué variables son más desfavorables para el
VAN.
3.- Con la información obtenida en el punto anterior la empresa se puede plantear si le compensaría o no
incurrir en costes adicionales para obtener información de aquellas variables cuya variación más afecta al VAN.

46. 28
2.26 VALOR DE LA INFORMACION
Se puede eliminar algo de incertidumbre mediante la inversión en tiempo o dinero antes de que la empresa
realice el desembolso de la inversión. Sobre todo en las estimaciones pesimistas, por ejemplo el coste variable
unitario, se ha incrementado en 200 euros ante el temor de que una máquina determinada no funcione como
debiera y que dicho proceso se tuviera que realizar con otros métodos lo que supondría un incremento de coste
Coste de Capital 10,00%
Valor actual Renta 6,144567106
DATOS DE LA INVERSION
Inversión 150.000.000
Precio unitario 3.750
Coste variable unitario 3.000
Costes fijos 30.000.000
Impuestos 50%
Amortización 10%
Duración / Años 10
PESIMISTA NORMAL OPTIMISTA PESIMISTA NORMAL OPTIMISTA
Tamaño del mercado (A) 9.000.000 10.000.000 11.000.000 11.294.887 34.337.013 57.379.140
Cuota de mercado (B) 0,40% 1,00% 1,60% -103.915.747 34.337.013 172.589.773
Precio unitario (C) 3.500 3.750 3.800 -42.470.076 34.337.013 49.698.431
Coste variable unitario (D) 3.600 3.000 2.750 -150.000.000 34.337.013 111.144.102
Costes fijos (E) 40.000.000 30.000.000 20.000.000 3.614.178 34.337.013 65.059.849
OBTENCION DE LOS FLUJOS NETOS DE CAJA
ESTIMACION PESIMISTA
A B C D E
Año 0 Años 1 a 10 Años 1 a 10 Años 1 a 10 Años 1 a 10 Años 1 a 10
Ventas 337.500.000 150.000.000 350.000.000 375.000.000 375.000.000
Coste variable 270.000.000 120.000.000 300.000.000 360.000.000 300.000.000
Coste fijo 30.000.000 30.000.000 30.000.000 30.000.000 40.000.000
Amortización 15.000.000 15.000.000 15.000.000 15.000.000 15.000.000
Bº antes de impuestos 22.500.000 -15.000.000 5.000.000 -30.000.000 20.000.000
Impuestos 11.250.000 -7.500.000 2.500.000 -15.000.000 10.000.000
Amortización 15.000.000 15.000.000 15.000.000 15.000.000 15.000.000
Flujo de Caja -150.000.000 26.250.000 7.500.000 17.500.000 0 25.000.000
Valor Actual neto 11.294.887 -103.915.747 -42.470.076 -150.000.000 3.614.178
ESTIMACION OPTIMISTA
A B C D E
Año 0 Años 1 a 10 Años 1 a 10 Años 1 a 10 Años 1 a 10 Años 1 a 10
Ventas 412.500.000 600.000.000 380.000.000 375.000.000 375.000.000
Coste variable 330.000.000 480.000.000 300.000.000 275.000.000 300.000.000
Coste fijo 30.000.000 30.000.000 30.000.000 30.000.000 20.000.000
Amortización 15.000.000 15.000.000 15.000.000 15.000.000 15.000.000
Bº antes de impuestos 37.500.000 75.000.000 35.000.000 55.000.000 40.000.000
Impuestos 18.750.000 37.500.000 17.500.000 27.500.000 20.000.000
Amortización 15.000.000 15.000.000 15.000.000 15.000.000 15.000.000
Flujo de Caja -150.000.000 33.750.000 52.500.000 32.500.000 42.500.000 35.000.000
Valor Actual Neto 57.379.140 172.589.773 49.698.431 111.144.102 65.059.849
ESTIMACION NORMAL
A
Año 0 Años 1 a 10
Ventas 375.000.000
Coste variable 300.000.000
Coste fijo 30.000.000
Amortización 15.000.000
Bº antes de impuestos 30.000.000
Impuestos 15.000.000
Amortización 15.000.000
Flujo de Caja -150.000.000 30.000.000
Valor Actual Neto 34.337.013
VAN

47. 29
de 200 euros, aunque la posibilidad de que esto ocurra por ejemplo es del 10%. Pero si ocurre, se produciría
un flujo de caja después de impuestos de: que disminuiría el VAN.
Unidades vendidas x incremento coste x (1-t) = 100.000x200x0.5 = 10.000.000
Que disminuiría el VAN en: ∑
( )
El nuevo resultado del VAN sería: VAN: 34.3 – 61.4 = - 27,1
Este mayor coste hay que compararlo con el coste de mantenimiento o de revisión de la máquina, por ejemplo,
supongamos un coste de 100.000. Se trata de realizar un pago de 100.000 para evitar un pérdida de 61.4
millones que tiene una probabilidad de ocurrencia del 10%, si comparamos:
-100.000 +0.10*61.400.000 = 6.040.000 este sería el valor de la información adicional.
El inconveniente del análisis de sensibilidad es suponer que las variables actúan de forma independiente
cuando en la práctica no ocurre así: Si aumenta la cuota de mercado lo más probable es que aumente la
demanda y por tanto se puede aumentar el precio. Si se incrementa el precio por causa de la inflación lo
normal es que también afecte al coste variable unitario. En la práctica es muy improbable obtener los resultados
expresados en el cuadro resumen de los VAN.
2.27 ANALISIS DE ESCENARIOS
El análisis de sensibilidad del apartado anterior presenta como otros modelos vistos anteriormente algunos
inconvenientes:
1.- La asignación de los valores optimistas y pesimistas de las variables se asignan de forman subjetiva.
2.- Al mantener fijas las otras variables cuando cambia una de ellas estamos suponiendo que no existe una
dependencia entre ellas. En la práctica no ocurre así, las variables están todas relacionadas entre sí, una
disminución en el tamaño del mercado afectaría al precio de venta de los outputs y al precio de compra de
los inputs.
3.- Sólo ofrece los distintos resultados del VAN en función de la variación de una variable manteniendo fijas
las demás, siendo el decisor el que adopte una decisión de acuerdo con la información facilitada y de su
actitud frente el riesgo.
En el análisis de escenarios también se asignan valores pesimistas y optimistas a las variables (escenario
pesimista, previsto y normal) pero a la hora de obtener el VAN combina los valores de las variables de los
distintos escenarios. Este método presenta también el inconveniente de asignar de forma subjetiva los
valores pesimistas y optimistas.
2.28 ANALISIS DEL PUNTO MUERTO
Consiste en aplicar la expresión que permite obtener el riesgo económico de una empresa (el efecto que
producen los costes fijos operativos) al análisis de proyectos de inversión. El análisis del punto muerto o umbral
de rentabilidad es el nivel mínimo de ventas en unidades físicas necesario para cubrir todos los costes fijos
operativos anuales (Incluida la amortización) y los costes variables correspondientes a ese nivel de ventas. Con
los datos contables la expresión del umbral de rentabilidad es la siguiente:

48. 30
La aplicación del análisis del punto muerto a los proyectos de inversión consiste en obtener el número de
unidades vendidas necesarias para que la diferencia entre el valor actual de las entradas menos el valor actual
de los pagos permita obtener un VAN positivo, de forma que si no se alcanza dicho volumen de venta en
unidades el VAN será negativo, si se supera dicho volumen de ventas anuales el VAN será positivo y el
proyecto tendrá éxito.
En el Punto Muerto contable se incluye la amortización de la inversión inicial, dicha amortización no se puede
incluir en la obtención del Punto Muerto del VAN porque no contempla el coste de oportunidad de la inversión
inicial, es decir la rentabilidad que se deja de ganar por invertir en el proyecto de inversión. Hay que sustituir la
amortización por el Coste Anual Equivalente (CAE = pago anual que hay que recuperar teniendo en cuenta la
remuneración del desembolso inicial) de la inversión inicial. Para obtener el CAE utilizamos la siguiente
expresión:
El importe de este pago se suma a los otros pagos correspondientes a los costes fijos, costes variables e
impuestos. Al se mayor el CAE que la amortización anual el numero de unidades para alcanzar el equilibrio en
el VAN es mayor que en el punto muerto contable. Para obtener la expresión del punto muerto del VAN
partimos de la siguiente igualdad:
IT = CT igualdad donde el VAN es igual a cero.
IT = (P – Cv)xQx(1-t)
CT = CAE + CFO(1-t) – At = CAE + CFO – t(CFO + A)
(P – Cv)xQx(1-t) = CAE + CFO – t(CFO + A)
Donde:
t = tasa impositiva
A = amortización anual
CFO = costes fijos operativos
CAE = coste anual equivalente
Q = número de unidades que hay que vender para alcanzar el punto muerto.
Despejando Q podemos calcular el número de unidades que hay que vender para alcanzar un volumen de VAN
= 0:
Q
- ( )
( - )( - )

49. 31
Ejemplo:
2.29 ARBOLES DE DECISIÓN
Un árbol de decisión es una representación gráfica de los posibles resultados de una inversión. Cada resultado
va acompañado de los cálculos correspondientes. Así, la dirección de la empresa puede enfrentarse
esquemáticamente con gran parte de la información relevante.
Para comprender la utilidad de los árboles de decisión conviene tener en cuenta que las empresas tienen que
modificar continuamente sus decisiones de inversión (llegando, a veces, hasta el punto de abandonarlas). Las
decisiones del futuro dependen de las tomadas anteriormente, por lo que las decisiones de hoy deben depender
de que lo sean posible mañana.
Para que un árbol de decisión sirva para valorar un proyecto, es necesario atribuir probabilidades de ocurrencia
a los distintos sucesos que provocarán una determinada decisión. Por otra parte, cuando la secuencia de
decisiones ha de tener lugar a lo largo de un determinado número de años o cuando las ramas del árbol que
representan las acciones alternativas y sus resultados adquieren distinta longitud, la manera de valorar y
comparar las distintas estrategias ha de descansar en el VAN. Lo mismo hay que decir cuando se trata de
determinar el valor esperado del proyecto, éste vendrá dado por el valor medio, según la distribución de
probabilidad, de los distintos VAN a que conduzcan las distintas ramas del árbol.
Coste de Capital 10,00%
Valor actual Renta 6,144567106
DATOS DELA INVERSION
Inversión 150.000.000
Precio unitario 3.750
Coste variable unitario 3.000
Costes fijos 30.000.000
Impuestos 50%
Amortización 10%
Duración / Años 10
ANALISIS DEL PUNTO MUERTO CONTABLE
VENTAS COSTE COSTES
UNIDADES VENDIDAS Años 1 a 10 VARIABLES MARGEN BRUTO FIJOS AMORTIZACIÓN BAT IMPUESTOS BDT
0 0 0 0 30.000.000 15000000 -45.000.000 -22.500.000 -22.500.000
25.000 93.750.000 75.000.000 18.750.000 30.000.000 15000000 -26.250.000 -13.125.000 -13.125.000
50.000 187.500.000 150.000.000 37.500.000 30.000.000 15000000 -7.500.000 -3.750.000 -3.750.000
60.000 225.000.000 180.000.000 45.000.000 30.000.000 15000000 0 0 0
75.000 281.250.000 225.000.000 56.250.000 30.000.000 15000000 11.250.000 5.625.000 5.625.000
85.000 318.750.000 255.000.000 63.750.000 30.000.000 15000000 18.750.000 9.375.000 9.375.000
100.000 375.000.000 300.000.000 75.000.000 30.000.000 15000000 30.000.000 15.000.000 15.000.000
150.000 562.500.000 450.000.000 112.500.000 30.000.000 15000000 67.500.000 33.750.000 33.750.000
200.000 750.000.000 600.000.000 150.000.000 30.000.000 15000000 105.000.000 52.500.000 52.500.000
Margen bruto unitario 750
Costes fijos totales 45.000.000
Punto muerto 60.000
ANALISIS DEL PUNTO MUERTO TESORERIA
COBROS PAGOS PAGOS Año 1 a 10 V.ACTUAL V. ACTUAL
UNIDADES VENDIDAS Años 1 a 10 Año 0 C.VARIABLE C.FIJO IMPUESTOS COBROS PAGOS V.A.N.
0 0 150.000.000 0 30.000.000 -22.500.000 0 196.084.253 -196.084.253
25.000 93.750.000 150.000.000 75.000.000 30.000.000 -13.125.000 576.053.166 714.532.103 -138.478.937
50.000 187.500.000 150.000.000 150.000.000 30.000.000 -3.750.000 1.152.106.332 1.232.979.952 -80.873.620
60.000 225.000.000 150.000.000 180.000.000 30.000.000 0 1.382.527.599 1.440.359.092 -57.831.493
75.000 281.250.000 150.000.000 225.000.000 30.000.000 5.625.000 1.728.159.498 1.751.427.802 -23.268.303
85.000 318.750.000 150.000.000 255.000.000 30.000.000 9.375.000 1.958.580.765 1.958.806.942 -226.177
100.000 375.000.000 150.000.000 300.000.000 30.000.000 15.000.000 2.304.212.665 2.269.875.651 34.337.013
150.000 562.500.000 150.000.000 450.000.000 30.000.000 33.750.000 3.456.318.997 3.306.771.351 149.547.646
200.000 750.000.000 150.000.000 600.000.000 30.000.000 52.500.000 4.608.425.329 4.343.667.050 264.758.280

50. 32
Un árbol de decisión es un grafo en el que se representan las distintas alternativas de inversión que se le
plantean al sujeto decisor así como los posibles resultados que obtendría en función de los distintos estados de
la naturaleza que puedan presentarse. Todo árbol se compone de una seri de elementos como son: nudos que
se unen mediante ramas, arcos o flechas.
Sobre las ramas se representan bien las distintas opciones de inversión posible o bien los diferentes estados de
la naturaleza que puedan suceder. Las ramas tienen su origen en nudos, existiendo dos tipos de nudos: nudos
decisionales y nudos aleatorios.
Un nudo decisional se representan mediante un cuadrado y de él parten las distintas alternativas que puede
tomar el decisor en un momento dado junto con el resultado esperado de dicha alternativa. La elección
consistirá en elegir aquela alternativa que presente un mayor resultado.
Un nudo aleatorio se representa por medio de un círculo y de él parten los posibles estados que puede
presentar la naturaleza dependiendo de las distintas alternativas de inversión,
Una vez obtenida la estructura del árbol, se valoran todas las ramas de derecha a izquierda, hasta llegar a un
nudo aleatorio. El valor del nudo aleatorio se obtiene mediante la esperanza matemáticas de todas las ramas
que salen de dicho nudo. Una vez valorado los nudos aleatorios lo siguiente es elegir aquella alternativa de
inversión que presenta un mayor valor monetario esperado.
2.30 SIMULACIÓN ESTADÍSTICA
Los métodos que hemos estudiado para tratar de eliminar el riesgo en las decisiones de inversión son limitados
en cuanto a las distintas posibilidades que ofrecen para poder tomar una decisión. Por ejemplo, el empleo de un
coeficiente que transforme los flujos netos de caja arriesgados en flujos de caja equivalentes a un flujo cierto,
proporciona un único valor para el VAN del proyecto. Lo mismo hace el empleo de un tipo de descuento más
elevado para hacer frente a un riesgo más alto. El análisis de la sensibilidad permite estudiar el efecto del
cambio en una variable en un momento dado. En cambio, la utilización de la simulación estadística permite
considerar todas las combinaciones posibles.
2.30.1 SIMULACIÓN DE MONTECARLO
Consiste en un muestreo artificial o simulado. Remplazando el universo real por el universo teórico
correspondiente, descrito por una ley de probabilidad que se supone conocida y luego se obtiene una muestra
de la población teórica mediante una sucesión de números aleatorios, convirtiéndose en observaciones de la
variable o variables.

51. 33
En una simulación las variables importantes pueden, por ejemplo, ser las siguientes:
- Referentes a la inversión: Desembolso inicial Q0, y el Valor residual.
- Referentes al horizonte económico: t
- Referente a los flujos netos de caja, desglosando:
Ingresos: Tamaño del mercado, Crecimiento del mercado, Cuota de mercado en unidades físicas, precio de
venta.
Costes: Costes fijos, costes de explotación
La aplicación del método es la siguiente:
1. - Obtención de un modelo preciso del proyecto.
2. - Para cada variable obtenemos su función de densidad de probabilidad. Esta función la podemos obtener de
la observación del comportamiento en el pasado de la variable o bien, si no disponemos de ninguna
información, podemos obtener del universo real una muestra que nos permita inferir la ley de probabilidad
correspondiente.
3. - Se elige al azar un número comprendido entre 0 y 1, con tantos decimales como se desee. Dicho número
puede extraerse de una tabla de números aleatorios.
4. - Cada número aleatorio se lleva sobre la columna de probabilidad acumulada y sería el correspondiente
valor de la variable.
5. - Se repite el experimento hasta obtener el número deseado de valores muestrales.
6. - Cuando una magnitud es considerada como cierta, permanece constante en el modelo.
2.31 ANÁLISIS PROBABILÍSTICO DE UNA SOLA INVERSIÓN ARRIESGADA
Se puede establecer una relación entre el estado futuro esperado de la economía y los rendimientos
provenientes de las inversiones de las empresas. La relación que existe entre los distintos niveles de
rendimiento y su función relativa da lugar a una distribución de probabilidad. Las distribuciones de
probabilidad contienen el conjunto de todos los posibles resultados de un suceso en particular. Podemos
suponer una distribución de resultados que se ajuste mucho a una distribución normal de la forma:
Pr
Rendimientos
Una característica importante de la distribución normal es que puede definirse completamente con dos
parámetros: media o rentabilidad esperada E(R) y la desviación típica  .
Se define la rentabilidad esperada como:
jP
nj
1j
jRE(R) 


 indica la media de la distribución de probabilidad de los posibles resultados.
Y, su desviación típica como:

52. 34
  jPE(x))j(x
2
 es una medida de la dispersión de la distribución de probabilidad. Cuanto menor sea la
desviación típica, la distribución está más concentrada y, en consecuencia, menos arriesgado.
Cuando trabajamos con una distribución de probabilidad, una medida adecuada del riesgo de la distribución
es el coeficiente de variación =
)jE(R
j
que nos mide la desviación típica por unidad de rendimiento, de esta
forma utilizamos una medida normalizada del riesgo de una activo individual. La utilidad de esta medida
consiste en que permite comparar el riesgo de dos proyectos que tienen tamaño diferente.
Conociendo la esperanza y la desviación típica, y suponiendo que estamos en una distribución normal de
probabilidad, podemos obtener la probabilidad de que un determinado rendimiento caiga dentro de un
determinado intervalo. Para ello transformamos la distribución normal: N(E(R); (R)) en una N(0,1) que se
encuentra tabulada. El procedimiento se llama tipificación o estandarización de la distribución: y se obtiene:
)(
)(
r
RER
z



Supongamos dos activos A y B con la siguiente distribución de rendimientos en pesetas:
Estado
Economía
Rendimientos
Pr. A B E(A) E(B) (A-E(A))^2Pr (B-E(B))^2Pr
Recesión 0,2 400 300 80 60 2000 8000
Estabilidad 0,6 500 500 300 300 0 0
Crecimiento 0,2 600 700 120 140 2000 8000
Valor esperado 500 500
Varianza 4000 16000
Desviación típica 63,25 126,49
Si suponemos que los rendimientos de los proyectos A y B se distribuyen de manera normal, las
distribuciones de probabilidad de los dos activos son las que aparecen a continuación. El rendimiento
esperado para los dos activos es de 500, sin embargo la gráfica más plana corresponde al activo B, indica
que éste es más arriesgado.
ACTIVO B
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
200 300 400 500 600 700 800
Rendimientos
Probabilidad

53. 35
Supongamos que queremos determinar la probabilidad de que el rendimiento real del activo A se encuentre
dentro del intervalo de 450 a 575. El primer paso consiste en calcular los valores de z correspondientes a los
límites del intervalo para el proyecto:
        %82.666682.02148.08830.079.019.119.179.0575450
19.1
25.63
500575
sup
79.0
25.63
500450
inf







ZPZPZPARP
eriorlimite
eriorlimite
2.32 CÁLCULO DE LA ESPERANZA Y DE LA VARIANZA DEL VAN
Una característica de los proyectos de inversión es que su duración exceda más de un período, abarcando
varios períodos. En condiciones de falta de información, los resultados de cada período no tienen un único
valor sino que, en cada período estos pueden asumir varios valores, cada uno con una probabilidad. Es decir,
los resultados de cada período son una variable aleatoria. Para evaluar estos proyectos plurianuales
necesitamos determinar los valores esperados y la desviación standard de todos los resultados. Para ello
seguiremos las siguientes etapas:
1º. - Estimación del valor esperado de los posibles resultados de los F.N.C. de cada período.
P
r
tQ
r
t
h
1=r
=)Qt
E( 
Donde h es el número de posibles resultados de cada período.
2º) Actualizar los valores esperados obtenidos al momento inicial para obtener el valor esperado del proyecto.
De esta manera obtendremos la distribución de probabilidad del proyecto, que vendrá dada por la siguiente
expresión:
)
t
k+(1
)Qt
E(n
1=t
+)Q0
-E(=E(VAN) 
El valor de la desviación standard y por tanto del grado de riesgo, será diferente según que, los distintos flujos
netos de caja del proyecto sean independientes o estén correlacionados período a período.
Para estudiar la desviación standard utilizaremos el modelo de F. S. Hillier(1963). En dicho modelo se
distinguen tres casos:
ACTIVO A
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
200 300 400 500 600 700 800
Rendimientos
Probabilidad

54. 36
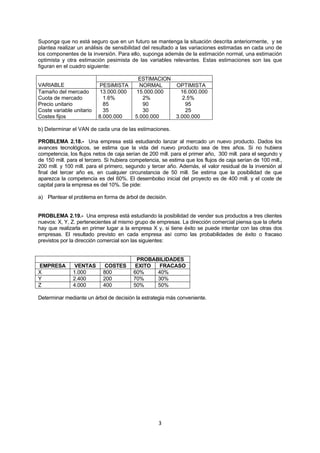
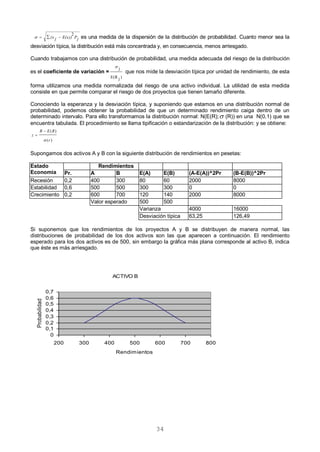
a) Los flujos netos de caja son independientes:
Esto implica que la distribución de probabilidad de los F.N.C. de cada período son completamente
independientes. Es decir, el F.N.C. del periodo t no depende de lo ocurrido en el periodo (t-1) y tampoco influye
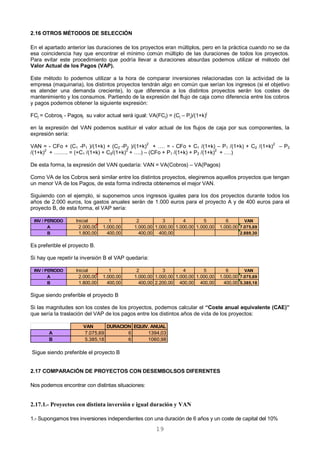
en el F.N.C. del periodo (t+1). Por tanto, su varianza será:
k)+(1
2t
)Qt
(2n
1=t
+)Q0
(2=(VAN)2 
 
Y su desviación standard: Var(VAN)(VAN) 
Donde el valor de:
P
r
t])Qt
-E(Q
r
t
[
h
r=
)=Qt
(
2
1
2

b) Los flujos netos de caja están correlacionados período a período:
Suponer que todos los F.N.C. esperados son independientes de un período a otro no es una posición realista
ya que, en la gran mayoría de proyectos de inversión dependerán aunque sólo sea parcialmente de los F.N.C.
de los períodos anteriores. Si en un proyecto de inversión se producen buenos resultados en los primeros
años, existe una probabilidad muy alta que en los resultados obtenidos en los años siguientes sean mayores
que los esperados en un principio.
Un caso extremo consiste en suponer que los resultados de un proyecto están perfectamente correlacionados
período a período, es decir, que el resultado de un período se puede considerar como una función lineal de los
resultados de los otros períodos.
Para este caso la varianza sería:
]
2
)
n
k+(1
)Qn
(
+....+
)
2
k+(1
)Q2
(
+
k)+(1
)Q1
(
+)Q0
([=(VAN)2


Y su desviación standard: )()( VANVarVAN 
c) Los flujos netos de caja están correlacionados pero de una forma imperfecta:
Este caso es intermedio entre los dos anteriores ya que, en cualquier proyecto de inversión sus F.N.C. ni son
completamente independientes ni perfectamente correlacionados sino que, tienen algún grado de correlación
entre ellos.
El modelo de Hillier descompone cada F.N.C. en dos componentes, un componente que varía
independientemente de cualquier F.N.C. de otro período, y otro componente que está perfectamente
correlacionado con cualquier otro período: Qt = Qt
´
+Qt
´´
siendo:
Qt
´
= la parte que varía independientemente.
Qt
´´
= la parte que está perfectamente correlacionada.
Por tanto, la varianza del proyecto sería:
]
2
)
t
k+(1
)Qt
(n
1=t
+)Q0
([+
)
2t
k+(1
)Qt
(2n
1=t
+)Q0
(2=(VAN)2








2.33 COMPORTAMIENTO PROBABILISTICO DEL VALOR ACTUAL NETO
Al considerar los flujos netos de caja como variables aleatorias, estas podían ser entre sí independientes o bien
estar correlacionadas. De cada F.N.C. aleatorio obteníamos su esperanza y su varianza. En el supuesto de

55. 37
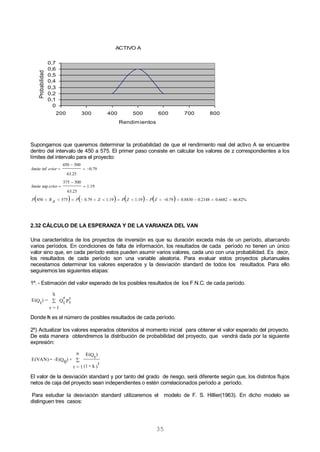
que estos F.N.C. fueran independientes, su suma da lugar a otra variable aleatoria llamada VAN con una
distribución que tenderá a ser normal, de la cual se puede calcular su media y su varianza, cuando el número
de sumandos tiende a infinito, la variable aleatoria VAN se aproximará a una: N[E(VAN);  (VAN)] y su
tipificada se aproximará asintóticamente a la distribución N(0,1). Esto se produce en virtud del teorema central
del límite. La convergencia de este teorema es bastante rápida y por ello, cuando el número de sumandos es
igual o superior a diez ya se puede utilizar la aproximación normal.
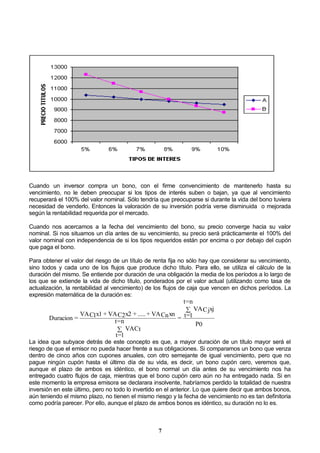
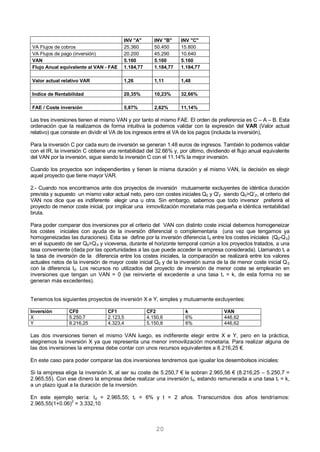
Se puede transformar cualquier distribución normal dada de la variable aleatoria VAN en una nueva variable
aleatoria z definiendo la nueva variable aleatoria normalizada correspondiente a VAN como:
)(
)(
VAN
VANEVAN
z



Esta variable aleatoria z tiene una distribución normal de E(t)= 0 y  (t)=1. La letra z recibe el nombre de
desviación standard normalizada y con ella se puede "standarizar" una distribución normal.
Si suponemos que la distribución de varios resultados de un proyecto es normal, podemos obtener el riesgo del
proyecto asignando probabilidades a los resultados más alto y más bajo del proyecto, ya que, dadas estas
probabilidades podemos encontrar el valor correspondiente de z en la tabla de distribución normal o de Gauss.

56. 1
PROBLEMAS DE INVERSIONES
PROBLEMA 2.1. - Dada la inversión definida por los siguientes flujos netos de caja
AÑO 0 1 2 3 4
F.N.C -10000 2000 3000 4000 5000
a) Calcular su VAN para un coste de oportunidad del capital del 10%. (717,85)
b) Calcular la TIR. (12,498%)
c) Calcular el Indice de Rentabilidad.(1,0717)
d) Calcular el Pay-back descontado.(4 años)
PROBLEMA 2.2.- Dadas las inversiones mutuamente excluyentes, recogidas en la tabla, y para
un tipo de actualización o descuento del 10 por 100, se pide:
Flujos netos de caja
Inversión 0 1 2 3 4 5
A -1.500 150 1350 150 -150 -600
B -1.500 0 0 450 1050 1950
C - 1.500 150 300 450 600 1875
D -1.500 300 450 750 750 900
1.- Calcular el VAN.
2.- Calcular el pay-back descontado.
3.- Calcular la TIR.
4.- Calcular el índice de rentabilidad.
Inversión VAN PBD TIR IR
A -610,24 --- --- 0,593
B 766,05 5 años 20.92% 1,51
C 796,42 5 años 22.79% 1,53
D 779,20 4 años 25.38% 1,519
PROBLEMA 2.3.- Su empresa está considerando cuatro posibles alternativas de inversión,
cuyos flujos netos de caja y desembolso inicial se detallan a continuación.
Periodo A B C D
0 -15000 -12500 -10000 -11800
1 6000 6000 3200 4000
2 6000 5000 4500 5500
3 6000 5000 5000 5500
4 2800 3500 5000 4000
a) Determine si se aceptan o rechazan los proyectos anteriores según los criterios del PR,
PRD, VAN, IR y TIR, si el plazo máximo establecido por la empresa para recuperar el
capital invertido es de 3 años y el coste de capital el 8%.
b) Si los proyectos fuesen independientes y la empresa dispusiera de un capital para invertir
de 25.000 u.m., ¿qué proyectos llevaría a cabo?
c) Si los proyectos fuesen excluyentes, ¿cuál debería elegir la empresa? Razone su
respuesta.
Inversión PRD VAN IR TIR
A
B
C
D
3 años
3 años
3 años
3 años
2.520,67
3.884,02
4.465,30
3.925,26
1,168
1,31
1,446
1,33
16.08%
22.52%
25.25%
22.04%

57. 2
PROBLEMA 2.4.- Una inversión requiere un desembolso inicial de 2.000 u.m. y genera, durante
cada uno de los cinco años de su duración, un flujo anual constante de 600 u.m. Siendo el tipo de
actualización del 10 por 100, se desea conocer su valor actual neto y su tasa de rentabilidad
(274,47€; 15,24%).
PROBLEMA 2.5.- Una empresa se plantea realizar un proyecto que generará unos cobros
anuales de 2000 euros y unos pagos de 1300 euros. El desembolso inicial es de 1000 euros, la
vida de 5 años y el tipo impositivo del 30%. Además el proyecto se financiará con un préstamo
a 5 años, siendo los pagos por intereses y devolución del principal de 277,40973 euros cada
año. El tipo de interés es del 12%. Obtener el VAN si el equipo se deprecia linealmente. (VAN =
982,63 €)
PROBLEMA 2.6.-: La Empresa Z y X S.A. que desea incrementar sus ventas dadas las
posibilidades de aumentar su segmento de mercado, ha de estudiar las alternativas de proyectos
de inversión que se le ofrecen para producir la cifra necesaria. Esta producción se calculará sólo
por tres años, época en la que habrá de sustituir sus productos tradicionales por otros de nueva
tecnología. La Empresa puede elegir entre tres proyectos de inversión con los siguientes datos (en
mill. de €):
PROYECTO A: Coste inicial: 90; Ingresos estimados como cobros: 1º año 80, 2º año 95, 3º año
105. Gastos estimados anuales (pagos): 50. (VAN = 7.99)
PROYECTO B: Coste inicial: 75; Ingresos estimados anuales (tres años) como cobros 80; Gastos
estimados anuales (pagos): 45. (VAN = 5.82)
PROYECTO C: Coste inicial: 120; Ingresos estimados como cobros 1º y 2º año 130, 3º año 110.
Gastos estimados (pagos), 1º y 2º año 70; 3º año 80 (VAN = - 0.13)
Se pide elegir el proyecto de inversión que ofrezca el máximo valor actual neto VAN,
teniendo en cuenta que:
- El Impuesto sobre sociedades es del 25 %
- El standard mínimo de rentabilidad exigido a las inversiones es 10%.
PROBLEMA 2.7 : Una empresa, dentro de su plan de inversiones, acomete la instalación de un
equipo industrial de las siguientes características:
- Valor de adquisición: 5.000.000 €.
- Forma de pago: 3.000.000 €. a su instalación; 1.000.000 €. al cumplir el primer año; 1.000.000 €.
al cumplir el segundo año.
- Producción real prevista: 200.000 unidades anuales que a un precio unitario de 20 €.
- Costes de producción para la producción prevista anual:
Pagos por materias primas 1.000.000
Pagos por mano de obra 1.200.000
Pagos por gastos generales de fabricación 800.000
Duración inicial prevista: 8 años
La casa suministradora del equipo industrial, ofrece las siguientes alternativas en cuanto a
recompra (y duración por tanto) del equipo:
1º. Al final del octavo año ofrece por el equipo 1.500.000 €.
2º. Al final del noveno año ofrece 1.000.000 €.
3º. Al final del décimo año 500.000 €.
El prolongar la vida del equipo por encima de los ocho años, acarrearía gastos adicionales
por reparaciones y mayores consumos, que serían:
en el noveno año gastos por 250.000 €.
en el décimo año gastos por 200.000 "
Se pide: Determinar cual será el tiempo de utilización más favorable por el criterio del Valor actual
neto, sabiendo que el coste de capital para la empresa es del 7% antes de impuestos.
VAN (8 AÑOS) = 2.036.294,-
VAN (9 AÑOS) = 2.115.164,39
VAN (10 AÑOS) = 2.232.084,73

58. 3
PROBLEMA 2.8.- Una empresa está estudiando el lanzamiento de un nuevo producto al
mercado. El coste de la inversión será de 1.000.000 € y al final de su vida útil se venderá por
200.000€. Se tienen los siguientes datos de la inversión:
Año Ventas en
unidades
Precio venta
unitario
Coste variable
unitario
Coste fijo
1 4000 200 120 55000
2 6000 200 120 55000
3 7000 200 120 55000
4 7500 180 120 55000
5 6000 180 120 55000
6 5500 180 120 55000
7 4500 170 120 55000
8 4000 170 120 55000
Se sabe además que: la amortización a practicar será la lineal, que en el momento
inicial existirán unas necesidades de capital circulante de 250.000 € recuperándose dicho
capital circulante al final de la inversión. El coste de capital para la empresa es del 10% y la
tasa impositiva para la empresa es del 30%.
Se pide:
1.- Calcular el VAN del proyecto (338.567,49€).
2.- Calcular la TIR del proyecto (16,745%).
3.- Calcular el pay back descontado (7 AÑOS).
4.- Calcular el índice de rentabilidad (127,085%).
PROBLEMA 2.9.- Una empresa dispone de un nuevo proyecto de 5 años de duración. El
responsable financiero ha elaborado las siguientes cuentas de resultados para cada uno de los
5 años, “sin” y “con” el proyecto propuesto, que se mantendrán constantes durante la vida de la
inversión.
Concepto “Sin” Proyecto “Con” Proyecto
Ingresos = Cobros
Costes variables= Pagos
Depreciación
Impuestos
Beneficio Neto
1.000
500
300
-100
100
1.100
210
460
-215
215
El desembolso inicial del proyecto es de 800 u.m., el tipo de interés es del 9% y el sistema de
amortización seguido es lineal. Obtener el VAN del proyecto. (Interesa realizar la inversión, el
valor de la empresa se incrementa en 269,65 €)
PROBLEMA 2.10.- Una empresa esta estudiando la compra de una nueva maquinaria para
incrementar su producción. Los datos económicos de la nueva máquina son los siguientes:
- Coste de la máquina: 4.000.000 €; vida útil 7 años, al cabo de los cuales tendrá un valor
residual de 500.000€. la amortización a practicar es por el método lineal.
- Los ingresos por ventas serán de 20.000€ por hora de trabajo efectiva. Por las características
de la producción la utilización efectiva de la máquina será del 40% del tiempo de trabajo.
- Tiempo de trabajo: Estará formado por tres turnos diarios de 8 horas cada uno. Se trabajarán
cinco días a la semana y, el número de semanas trabajadas en el año será de 47.
- Otros costes: Los gastos diarios de mantenimiento de la máquina serán de 40.000€ . El coste
de la mano de obra empleada será de 6.000€ por hora. Los gastos de revisión y mantenimiento
anual serán de 100.000€.
Si la tasa impositiva es del 30% y el coste de capital para la empresa es del 8%, ¿interesaría
comprar la máquina, Cuál sería el VAN del proyecto?

59. 1
PROBLEMA 2.11.- Una empresa está estudiando el lanzamiento de un nuevo producto al mercado.
Los datos con los que trabaja el departamento de inversiones de la empresa son los siguientes:
Año Inversión Coste fijo Coste variable unid. Unid.vendidas Precio venta
unidad
0
1
2
3
900.000
100.000
1.300.000
350.000
0.60
0.7
0.9
1.000.000
1.100.000
1.200.000
1.5
1.7
2.0
Sabiendo que el coste de capital para la empresa es el 11%, se pide:
1.- Calcular el VAN y la TIR del proyecto de inversión.
2.- Suponiendo que la tasa de reinversión de los flujos intermedios de caja es del 6% ¿sigue siendo
interesante la inversión?.
3.- Vuelva a calcular el apartado 1, aplicando una amortización lineal al coste de la inversión siendo
su valor residual nulo y, suponiendo una tasa impositiva sobre los beneficios de la empresa del 35%.
PROBLEMA 2.12.- La empresa Prado va a sustituir una máquina por otra más moderna que cuesta
200 millones de u.m. La máquina antigua se compró hace cuatro años con un coste de 160 mill. En
la actualidad se puede vender por 25 mill de um...
La nueva máquina va a reducir costes en salarios y otros gastos, de forma que produzca una
diferencia de flujos de caja de 40 mill. al año, incrementando las ventas anuales en 20 mill. Se prevé
que este incremento de actividad aumente las necesidades operativas de fondos en 15 miil. Dicho
importe se recuperará al fina de su vida económica Su vida será de 4 años siendo su valor residual
de 25 mill. La amortización es lineal.
La máquina vieja iba a trabajar aún 4 años, al final de los cuales no tendría valor residual. Se
amortizaba también en línea recta.
Decidir si se debe o no sustituir la máquina vieja por la nueva, sabiendo que los impuestos ascienden al
25% del beneficio y que el coste de capital de la empresa es del 12%. (VAN: 15.275.765,53)
PROBLEMA 2.13.- Una empresa está estudiando sustituir su maquinaria antigua por otra nueva. La
maquinaria antigua costó 1.000 um. y viene siendo amortizada de forma lineal al 5%. A esta máquina
le quedan 10 años de vida, al final de los cuales no tendrá valor residual. La nueva máquina tendrá el
mismo coste que la antigua pero durará solamente la mitad de tiempo que la antigua, reducirá los
gastos anuales (que en la actualidad son de 1.500 um.) en 90 um. y tendrá los mismos cobros por
ventas, es decir, de 2.000 um. Siendo nulo su valor residual.
El coste de capital para la empresa es del 12% y la tasa impositiva es del 35%. Si decide
cambiar, el valor en el mercado de segunda mano de la máquina antigua es de 300 um. Se pide: a)
Calcular el VAN de mantener el quipo viejo ( 1.935,20 €)y b) el VAN si decide cambiar de equipo
(1.734,62 €).
PROBLEMA 2.14.- La empresa ABC fabricante de componentes eléctricos está estudiando implantar
una nueva línea de producción para atender un incremento en la demanda. Debe decidir entre dos
procesos productivos A y B, los costes y duración de dichos procesos son los siguientes:
Año Proceso A Proceso B
0
1
2
3
4
5
1.000.000
300.000
340.000
380.000
420.000
1.200.000
350.000
350.000
350.000
350.000
350.000
Teniendo en cuenta que el coste de capital es del 8%, calcular:
1.- Qué proceso productivo debe elegir la empresa suponiendo que una vez transcurrida la vida
económica no se renovarán.
2.- Qué proceso productivo debe elegir la empresa suponiendo que una vez transcurrida la vida
económica se renovarán los equipos.
3.- Suponiendo que una vez trascurrida la vida económica se renovarán los equipos, qué proceso
debe elegir la empresa suponiendo que la tasa impositiva es del 25%, que la amortización que aplica

60. 2
la empresa es la lineal, que al final de la vida económica se podrá vender el proceso A por 250.000€ y
el proceso B por 300.000€.
PROBLEMA 2.15 .- Una empresa está estudiando la posibilidad de efectuar una inversión en un nuevo
equipo industrial. Los datos de la inversión son los siguientes: Q0= -100, Q1= 20; Q2= 80 y Q3= 120. Coste
de capital para la empresa 7%. Estudiar la efectuabilidad de la inversión en los siguientes casos:
a) En ambiente de certeza.
b) Suponiendo que el proyecto de inversión se desarrollará en un ambiente de incertidumbre, obtener el
VAN en los siguientes casos:
b-1) considerar una prima de riesgo del 3%.
b-2) considerar los siguientes coeficientes de reducción de los flujos netos de caja a condiciones de
certeza: 80.03;85.02;95.01   .
PROBLEMA 2.16.- Tenemos los siguientes datos de un proyecto de inversión:
Inversión P.unitario Coste variable
unitario
Costes fijos Tasa impositiva Duración Amortiza
ción
150.000.000 3.750 3.000 30.000.000 50% 10 años Lineal
Cuota de mercado: 1%
Tamaño del mercado: 10.000.000 de consumidores
Cálculo de las unidades vendidas: cuota de mercado del producto x tamaño del mercado
Ventas: unidades vendidas x precio de venta.
Si el coste de capital para la empresa es del 10%. Se pide:
a) Determinar el VAN del proyecto.
Suponga que no está seguro que en un futuro se mantenga la situación descrita anteriormente, y se
plantea realizar un análisis de sensibilidad del resultado a las variaciones estimadas en cada uno de
los componentes de la inversión. Para ello, suponga además de la estimación normal, una estimación
optimista y otra estimación pesimista de las variables relevantes. Estas estimaciones son las que
figuran en el cuadro siguiente:
VARIABLE
ESTIMACION
PESIMISTA NORMAL OPTIMISTA
Tamaño del mercado
Cuota de mercado
Precio unitario
Coste variable unitario
Costes fijos
9.000.000
0.004
3.500
3.600
40.000.000
10.000.000
0.01
3.750
3.000
30.000.000
11.000.000
0.016
3.800
2.750
20.000.000
b) Determinar el VAN de cada una de las estimaciones.
PROBLEMA 2.17 - Tenemos los siguientes datos de un proyecto de inversión:
Inversión P.unitario Coste varia.unitario Costes fijos Tasa impositiva Duración Amortización
50.000.000 90 30 5.000.000 30% 8 años Lineal
Cuota de mercado: 2%
Tamaño del mercado: 15.000.000 de consumidores
Cálculo de las unidades vendidas: cuota de mercado del producto x tamaño del mercado
Ventas: unidades vendidas x precio de venta.
Si el coste de capital para la empresa es del 10%. Se pide:
b) Determinar el VAN del proyecto.

61. 3
Suponga que no está seguro que en un futuro se mantenga la situación descrita anteriormente, y se
plantea realizar un análisis de sensibilidad del resultado a las variaciones estimadas en cada uno de
los componentes de la inversión. Para ello, suponga además de la estimación normal, una estimación
optimista y otra estimación pesimista de las variables relevantes. Estas estimaciones son las que
figuran en el cuadro siguiente:
VARIABLE
ESTIMACION
PESIMISTA NORMAL OPTIMISTA
Tamaño del mercado
Cuota de mercado
Precio unitario
Coste variable unitario
Costes fijos
13.000.000
1.6%
85
35
8.000.000
15.000.000
2%
90
30
5.000.000
16.000.000
2.5%
95
25
3.000.000
b) Determinar el VAN de cada una de las estimaciones.
PROBLEMA 2.18.- Una empresa está estudiando lanzar al mercado un nuevo producto. Dados los
avances tecnológicos, se estima que la vida del nuevo producto sea de tres años. Si no hubiera
competencia, los flujos netos de caja serían de 200 mill. para el primer año, 300 mill. para el segundo y
de 150 mill. para el tercero. Si hubiera competencia, se estima que los flujos de caja serían de 100 mill.,
200 mill. y 100 mill. para el primero, segundo y tercer año. Además, el valor residual de la inversión al
final del tercer año es, en cualquier circunstancia de 50 mill. Se estima que la posibilidad de que
aparezca la competencia es del 60%. El desembolso inicial del proyecto es de 400 mill. y el coste de
capital para la empresa es del 10%. Se pide:
a) Plantear el problema en forma de árbol de decisión.
PROBLEMA 2.19.- Una empresa está estudiando la posibilidad de vender sus productos a tres clientes
nuevos: X, Y, Z. pertenecientes al mismo grupo de empresas. La dirección comercial piensa que la oferta
hay que realizarla en primer lugar a la empresa X y, si tiene éxito se puede intentar con las otras dos
empresas. El resultado previsto en cada empresa así como las probabilidades de éxito o fracaso
previstos por la dirección comercial son las siguientes:
PROBABILIDADES
EMPRESA VENTAS COSTES EXITO FRACASO
X 1.000 800 60% 40%
Y 2.400 200 70% 30%
Z 4.000 400 50% 50%
Determinar mediante un árbol de decisión la estrategia más conveniente.

62. PROBLEMA 2.20.- Una empresa está estudiando lanzar un nuevo producto al mercado, la inversión en maquinaria
de alta tecnología será de 3.000.000 € y la duración será de 5 años, al final de los cuales se podrá vender por
1.500.000 €. Los costes previstos durante cada uno de los 5 años son:
Costes variables:
Por compras
Por suministros
2.5 € por unidad vendida
3.5 € por unidad vendida
Costes fijos operativos
Gastos de personal 550.000
Se prevé para el primer año que las ventas en unidades sean de 38.000, con un incremento anual acumulativo del
15%. El precio por unidad será de 29 € y se mantendrá constante durante los cinco años. Tantos los costes como las
ventas se pagan/cobran al contado. La financiación del proyecto se realizará con recursos propios, el coste de los
recursos propios es del 7%, la tasa impositiva es del 25%. Con esta información le piden que calcule el VAN del
proyecto de inversión.
Teniendo en cuenta que, por las características del nuevo producto, es muy sensible a pequeñas variaciones en la
demanda, le piden que cuantifique para el primer año de la inversión el riesgo económico (medido por el umbral de
rentabilidad y el apalancamiento operativo) como consecuencia de la existencia de unos elevados costes fijos
operativos.
Suponiendo que efectivamente las ventas se incrementen en un 15% en el año siguiente, obtener el beneficio neto y
la rentabilidad financiera de dicho año.
PROBLEMA 2.21.- Suponga que presento a la Administración Pública dos instancias para opositar para el cuerpo de
gestión A y para el cuerpo de gestión B, preparándose durante mucho tiempo para las dos oposiciones. . La
Administración le comunica que mañana tiene convocados a la misma hora el primer ejercicio para las dos
oposiciones. Si aprobara la oposición para el cuerpo A ganaría 1.200 euros mensuales, si aprobara la oposición para
el cuero B ganaría 1.800 euros mensuales. De acuerdo con los conocimientos adquiridos tiene una probabilidad del
70% de aprobar el primer ejercicio de la oposición al cuerpo A y una probabilidad el 40% de aprobar el segundo
ejercicio. En cuanto al cuerpo grupo B, estima en un 40 % la probabilidad de aprobar el primer ejercicio y en un 50 %
la de aprobar el segundo ejercicio. En cualquiera de las dos oposiciones si no supera el primer ejercicio ya no puede
presentarse al segundo y suspende la oposición. Dado que no puede presentar al primer ejercicio de los dos grupos
al realizarse a la misma hora ¿a cuál debería asistir si desea maximizar su ganancia mensual?. ¿cuál sería en euros
el resultado esperado de dicha decisión?.

63. 1
Tabla de contenido
TEMA 2.2.- VALORACIÓN DE ACTIVOS FINANCIEROS............................................................. 2
2.2.1 UTILIDAD DE LA VALORACIÓN DE LAS OBLIGACIONES Y ACCIONES............................... 2
2.2.2 LAS OBLIGACIONES.............................................................................................................................. 2
2.2.3 LA VALORACIÓN DE LAS OBLIGACIONES .................................................................................... 3
2.2.3.1 Rendimiento de un bono.............................................................................................4
2.2.3.2 Títulos con reembolso fijo y cupón cero....................................................................4
2.2.3.3 Títulos con reembolso fijo y pago de cupones periódicos.......................................4
2.2.3.4 Rentabilidad efectiva de los títulos con cupones de periodicidad no anual ...........5
2.2.3.5 El cálculo del cupón corrido .......................................................................................5
2.2.4 ESTRUCTURA TEMPORAL DE LOS TIPOS DE INTERÉS Y RENTABILIDAD AL
VENCIMIENTO..................................................................................................................................................... 5
2.2.5 CÁLCULO DEL RIESGO DE UNA OBLIGACIÓN............................................................................. 6
2.2.6 OBLIGACIONES CONVERTIBLES..................................................................................8
2.2.7 LA VALORACIÓN DE ACCIONES ..................................................................................................... 10
2.2.7.1 Obtención de la tasa de rentabilidad de una acción ...............................................11
2.2.7.2 Valoración de las acciones ordinarias .....................................................................12
2.2.7.3 Modelos de dividendos constantes..........................................................................13
2.2.7.5 Modelo de crecimiento no constante .......................................................................13
2.2.7.6 Obtención de la tasa de crecimiento ........................................................................14
PROBLEMAS TEMA 2.2 ................................................................................................................................. 15

64. 2
TEMA 2.2.- VALORACIÓN DE ACTIVOS FINANCIEROS
2.2.1 UTILIDAD DE LA VALORACIÓN DE LAS OBLIGACIONES Y ACCIONES
El análisis de la valoración de acciones y obligaciones tiene una doble utilidad. En primer lugar,
ayuda a valorar los activos financieros que se encuentran en el mercado y además facilita las
decisiones de inversión financiera.
En segundo lugar, desde el punto de vista de una empresa que emite títulos, es interesante
conocer cómo valoran los inversores dichos títulos, pues la remuneración requerida por los
inversores para comprar los valores condiciona el coste de capital de la empresa.
Cuando un inversor compra acciones u obligaciones, debe hacerlo a un precio no excesivamente
elevado, con el fin de obtener un buen rendimiento. Metodológicamente, la inversión en valores o
inversión financiera recibe el mismo tratamiento que la inversión productiva ya estudiada. La
inversión financiera, está definida por las mismas magnitudes que la inversión productiva es decir,
por la inversión inicial, los flujos de caja, la vida de la inversión y el valor residual en su caso. El
precio de cualquier activo financiero viene dado por el valor actual de sus flujos de caja esperados,
incluso si la corriente de estos últimos no es conocida con certeza. Entendiendo por flujo de caja la
corriente de dinero líquido que se espera recibir a lo largo de la vida de la inversión financiera.
2.2.2 LAS OBLIGACIONES
.
Las obligaciones son títulos de deuda emitidos tanto por entidades públicas como privadas para
financiarse a largo plazo. El emisor se compromete a devolver el dinero recibido junto con sus
intereses en unas fechas determinadas. Los compradores de las obligaciones se convierten en
acreedores del emisor. Además de las obligaciones existen otros títulos de deuda como los bonos, los
pagarés y las letras. . Los pagarés y las letras son títulos a corto plazo con vencimiento a 18 meses
como máximo. Las obligaciones y los bonos son títulos a largo plazo.
Los bonos son títulos de deuda con un vencimiento máximo a cinco años, las obligaciones son títulos
de deuda con vencimiento superior a cinco años. La operativa financiera es similar, por ello, se
denomina a ambos títulos de deuda de forma genérica como obligaciones. Las características
relevantes que debe tener toda emisión de obligaciones que permita a los inversores tomar sus
decisiones así como, la determinación de su valor futuro son las siguientes:
- Valor nominal (C0) : es el importe de la deuda contraída por el emisor con el comprador de la
obligación.
- Precio de emisión (Pe): Es la cantidad que hay que pagar en el momento de la emisión para
adquirir el título. Si el precio de emisión coincide con el valor nominal se dice que la emisión se
ha realizado a la par, Si el precio de emisión es distinto al valor nominal existe una prima de
emisión. Si el precio de emisión es inferior al valor nominal, la emisión se ha realizado por
debajo de la par la prima de emisión es negativa, si el precio de emisión es superior al valor
nominal, la emisión se ha realizado por encima de la par la prima de emisión es positiva.
- Valor de amortización o reembolso (Cn): Es el importe que recibe el obligacionista al
vencimiento de la obligación, la amortización puede ser por el valor nominal o a la par o bien
con prima de reembolso en este caso sería sobre la para o bajo la par según que, el valor de
reembolso esté por encima o por debajo del valor nominal.
- Valor actual del título (P0): Es el precio o cotización de mercado al cual se puede vender o
comprar un título en un momento posterior a su emisión. Esta cotización depende de los tipos
de interés que existan en el mercado para título de igual riesgo y vencimiento.
- Cupón (i): Es la remuneración periódica (semestral, anual) que el emisor se compromete a
pagar al obligacionista, mediante la aplicación de un tipo de interés nominal variable o fijo
sobre el nominal de la obligación. También se denomina cupón al tipo de interés nominal

65. 3
aplicado. Existen emisiones de obligaciones que no cobran cupones durante la vida de la
obligación, esto se acumula al nominal y se cobran todos al vencimiento de la obligación, este
tipo de obligaciones se denominan cupón cero.
- Vencimiento (n): Es el momento en que el emisor devuelve el capital al obligacionista.
Las características del emisor de la obligación (Estado, Entidades Públicas, Empresas), nos determina
el grado de incertidumbre a la hora de obtener la corriente de flujos esperados. Por ello se supone que
los instrumentos de deuda emitidos por el Estado y las Entidades Públicas son totalmente seguros, lo
que quiere decir que los flujos de caja se van a recibir puntualmente en las fechas señaladas, por lo
que al rendimiento de estos activos se le denomina rendimiento libre de riesgo. Si el emisor fuera una
empresa privada existe cierto riesgo en el cobro de los flujos de caja futuros que se refleja en la
rentabilidad que exigirán los inversores y que se materializa en una prima por riesgo que se añade a la
rentabilidad que ofrecen las obligaciones sin riesgo. Los posibles riesgos que se puede encontrar un
inversor en obligaciones serían:
- Riesgo de insolvencia o riesgo de crédito: Es la posibilidad de que en un futuro el emisor no
pueda hacer frente a sus compromisos de pago de cupones y reembolso del capital.
- Riesgo de liquidez: Es la posibilidad de no poder vender el activo de una forma rápida y a un
precio razonable La existencia de un mercado organizado que garantice la liquidez de los
títulos así como el tamaño de la inversión facilitará una menor prima por liquidez.
- Riesgo de tipos de interés: Los cambios en los tipos de interés afectan al precio de la
obligación y por tanto a la rentabilidad que obtendría un inversor que quisiera vender la
obligación antes del vencimiento. Si la intención es mantener la obligación hasta el final, no le
afectaría este tipo de riesgo. La variación en los tipos de interés también provoca que el
inversor no conozca a priori el tipo de interés al que puede reinvertir los intereses períodos
recibidos.
- Riesgo financiero: Se incluyen en este tipo de riesgo las características propias de la emisión
como por ejemplo: la existencia o no de avales que garanticen la emisión, el grado de prioridad
de la deuda emitida respecto de otras emisiones, la existencia o no de amortización anticipada
Otro tipo de riesgo es el que atañe al poder adquisitivo de los flujos de caja futuros, es decir, el riesgo
de inflación. Este nos indica que cuando recibamos cada uno de los flujos de caja, su capacidad
adquisitiva ya no será la misma que si los hubiésemos recibido actualmente, provocando una
disminución en la rentabilidad real de la inversión.
2.2.3 LA VALORACIÓN DE LAS OBLIGACIONES
El valor de una obligación en el mercado, al igual que el valor de cualquier activo, vendrá dado por el
valor actualizado de todos los flujos de caja que la adquisición de las obligaciones puede generar. Las
obligaciones son activos financieros de renta fija que, se denominan bonos si su vencimiento es hasta
tres años y obligaciones cuando el plazo de vencimiento es superior a tres años. La inversión en
obligaciones al igual que la inversión en fondos públicos, es normalmente menos arriesgada.
El obligacionista recibe al final de cada período de tiempo una serie de flujos de interés establecidos
explícitamente a lo largo de la vida del título, de ahí su denominación de activos financieros con interés
explícito. Las obligaciones suelen tener un vencimiento fijo, aunque, cuando la empresa que las emite
utiliza el sistema de amortización por sorteo, el vencimiento es aleatorio, y también cabe la posibilidad
de que determinados valores de renta fija no tengan vencimiento (deuda perpetua).
El obligacionista puede desprenderse de sus obligaciones vendiéndolas en el mercado, con lo que
obtiene el último flujo de caja positivo de su inversión. El valor de reembolso o devolución de la
obligación suele conocerse anticipadamente.

66. 4
El valor de la obligación se obtiene de la corriente de ingresos generados tanto por el concepto de
intereses como del reembolso del título. Si llamamos:
C0= nominal del título.
n = años de vida del título.
i = tipo de interés de la emisión.
k = tipo de interés normal del mercado para títulos de características similares.
Cn= valor de reembolso del título.
P0= valor actual del título.
El valor actual de una obligación ordinaria también llamada obligación americana que paga un cupón
fijo y periódico y se amortizan en su totalidad al vencimiento vendrá dado por:
)
nk+(1
Cn+
)
jk+(1
iC0
n
1=j
=
)
nk+(1
Cn+
)
nk+(1
iC0+.....+
)
2k+(1
iC0+
k)+(1
i0
C
=P0 
siendo: C0 i, el interés a cobrar o cupón. Si los intereses se cobran: anual, semestral, trimestral,
tendremos el cupón anual, semestral, trimestral, etc.
El valor actual de un título P0 en un momento determinado del tiempo, depende de: los períodos que
faltan hasta su vencimiento, del valor de reembolso, de los cupones periódicos y de la tasa de interés
del mercado para los bonos con características similares. Si disminuye el tipo de interés del mercado
aumenta el valor del título y viceversa.
)
k-k+(1Cn+an/kiC0=P0
2.2.3.1 Rendimiento de un bono
Cuando nos referimos a los títulos de renta fija, también nos interesa calcular la rentabilidad que
obtendrá un bono si se mantiene hasta su vencimiento. La rentabilidad será aquella r que iguale su
precio actual con el valor actualizado de los cobros esperados. Para calcular dicho rendimiento
deberemos conocer el precio de mercado del bono en cuestión al día de hoy P0, también deberemos
conocer cuál va a ser el valor del cupón, cuándo se va a producir (anualmente, semestralmente, etc.) y
su precio de reembolso Pn.
)
-n
r+(1Cn+an/riC
0
=P
0
Para calcular su rentabilidad, distinguiremos entre distintas modalidades de títulos de renta fija:
2.2.3.2 Títulos con reembolso fijo y cupón cero
Se cobra el nominal más los intereses en el momento de su amortización.
1-)
P0
Cn(
n
1
=r;
P0
Cn=)
nr+(1;
r)+(1
n
1
=
Cn
P0;)
n-r+(1Cn=P0
2.2.3.3 Títulos con reembolso fijo y pago de cupones periódicos
Se van cobrando periódicamente los intereses y se reembolsa el nominal al final de la vida del título.
)
-nr+(1Cn+an/riC0=P0

67. 5
Supongamos que el título lo hemos comprado transcurrido s períodos desde su emisión. Hemos
tenido el título en nuestro poder: n-s períodos y, su valor actual será:
)
s)--(nr+(1Cn+a /rs)-(niC0=P0
2.2.3.4 Rentabilidad efectiva de los títulos con cupones de periodicidad no anual
Los cupones se pueden cobrar por semestres, trimestres, etc. El perceptor del cupón puede pensar
que su importe lo va a rentabilizar por el tiempo que falta para terminar el año. De tal forma, que, para
medir la rentabilidad anual hay que tener en cuenta tanto los cupones percibidos por el título, como los
intereses generados por los cupones que se perciben durante el año y, hasta el final de dicho año:
)
nk-
rk+(1Cn+a rknk/ikC0=P0
Y, una vez obtenido rk, obtenemos la tasa anual: (1+rk)k
=(1+r); r=(1+rk)k
-1
2.2.3.5 El cálculo del cupón corrido
El vendedor de bonos u obligaciones tiene derecho a una parte del próximo cupón a pagar por la
entidad emisora. El cupón corrido va creciendo diariamente desde el momento en que un bono corta
cupón hasta el día antes del nuevo corte. En ese momento el cupón vale cero.
El precio de los bonos suele cotizar ex cupón y separadamente figura el valor del cupón corrido, de tal
manera que el comprador deberá pagar tanto el precio como el valor de dicho cupón corrido. El
cálculo del cupón corrido (CC) es el siguiente:
CC = (Cupón x días transcurridos desde el ultimo cupón)/365
Precio total = P0 (valor del bono) + CC
2.2.4 Estructura temporal de los tipos de interés y rentabilidad al vencimiento
La estructura temporal de los tipos de interés describe la relación que existe entre los tipos de interés y
el vencimiento de emisiones de títulos de renta fija, que tienen las mismas características menos la
que hace referencia al plazo de tiempo hasta su vencimiento.
En los apartados anteriores hemos obtenido la rentabilidad de un título suponiendo que la tasa anual
de interés es la misma para todo el período de vida del título. En la realidad, el mercado no aplica el
mismo tipo de interés a todos los vencimientos. La rentabilidad que se exige a un cobro dentro de 1
año es distinta a la que se exige para un cobro dentro de 2 años y así sucesivamente. Teniendo en
cuenta esta circunstancia, el modo de valorar una obligación es aplicando un tipo de interés diferente
para cada vencimiento, la expresión es:
n)
0n
r+(1
Cn+iC0+....+
2)
02
r+(1
iC0+
)
01
r+(1
iC0=P0
Lo que nos daría la valoración del título teniendo en cuenta los flujos y los tipos de interés: r01, r02, ……
r0n . Estos tipos de interés se denominan tipos de interés al contado o spot, es la rentabilidad que se
recibe por mantener un activo financiero hasta su vencimiento, recibiendo en ese momento el importe
de la inversión más los intereses. Según la expresión para la valoración de la obligación, tenemos spot
a 1 año, spot a 2 años, etc.

68. 6
También podemos encontrar una tasa simple de descuento que nos produjera el mismo valor actual.
Esta tasa llamada rentabilidad al vencimiento, no es más que la rentabilidad del bono, la podemos
escribir como:
nr)+(1
Cn+iC0+....+
2r)+(1
iC0+
r)+(1
iC0=P0
Para calcular r sólo necesitamos conocer el precio de mercado en el día de hoy P0, cuál va a ser el
valor del cupón C0i y cuándo se va a producir (anual, semestral, etc.) y su precio de reembolso Cn.
Se puede interpretar la rentabilidad al vencimiento como el tipo de rendimiento compuesto a lo largo
de la vida de la obligación desde el supuesto de que los cupones se reinvierten a un tipo de interés
idéntico a dicho rendimiento. Si esto no se cumpliese, el rendimiento real obtenido a lo largo de la vida
del bono no coincidirá con el rendimiento hasta el vencimiento.
2.2.5 CÁLCULO DEL RIESGO DE UNA OBLIGACIÓN
Las obligaciones están sometidas al riesgo de tipo de interés, que puede ser definido como la
variación del precio teórico de la obligación cuando el tipo de interés del mercado varía un 1% (100
puntos básicos) hacia arriba o hacia abajo. El precio de un bono varía en función del plazo hasta el
vencimiento, salvo en el caso de que el cupón coincida con el rendimiento requerido, entonces su
precio será el valor nominal. Cuanto mayor es el plazo de un bono mayor es la sensibilidad ante una
subida o bajada de los tipos de interés. Supongamos que tenemos dos obligaciones de las siguientes
características:
Obligación A: vencimiento dentro de dos años, cupón 700 euros pagadero por anualidades vencidas,
precio de reembolso de 10.000 euros.
Obligación B: Vencimiento dentro de 10 años, cupón de 800 euros pagadero por anualidades
vencidas, precio de reembolso de 10.000 euros.
k 5% 6% 7% 8% 9% 10%
Título A
1 700 666,67 660,38 654,21 648,15 642,20 636,36
2 10700 9705,22 9522,96 9345,79 9173,53 9005,98 8842,98
Precio 10371,88 10183,34 10000,00 9821,67 9648,18 9479,34
Título B
1 800 761,90 754,72 747,66 740,74 733,94 727,27
2 800 725,62 712,00 698,75 685,87 673,34 661,16
3 800 691,07 671,70 653,04 635,07 617,75 601,05
4 800 658,16 633,67 610,32 588,02 566,74 546,41
5 800 626,82 597,81 570,39 544,47 519,95 496,74
6 800 596,97 563,97 533,07 504,14 477,01 451,58
7 800 568,55 532,05 498,20 466,79 437,63 410,53
8 800 541,47 501,93 465,61 432,22 401,49 373,21
9 800 515,69 473,52 435,15 400,20 368,34 339,28
10 10800 6630,26 6030,66 5490,17 5002,49 4562,04 4163,87
Precio 12316,52 11472,02 10702,36 10000,00 9358,23 8771,09

69. 7
Cuando un inversor compra un bono, con el firme convencimiento de mantenerlo hasta su
vencimiento, no le deben preocupar si los tipos de interés suben o bajan, ya que al vencimiento
recuperará el 100% del valor nominal. Sólo tendría que preocuparse si durante la vida del bono tuviera
necesidad de venderlo. Entonces la valoración de su inversión podría verse disminuida o mejorada
según la rentabilidad requerida por el mercado.
Cuando nos acercamos a la fecha del vencimiento del bono, su precio converge hacia su valor
nominal. Si nos situamos un día antes de su vencimiento, su precio será prácticamente el 100% del
valor nominal con independencia de si los tipos requeridos están por encima o por debajo del cupón
que paga el bono.
Para obtener el valor del riesgo de un título de renta fija no sólo hay que considerar su vencimiento,
sino todos y cada uno de los flujos que produce dicho título. Para ello, se utiliza el cálculo de la
duración del mismo. Se entiende por duración de una obligación la media de los períodos a lo largo de
los que se extiende la vida de dicho título, ponderados por el valor actual (utilizando como tasa de
actualización, la rentabilidad al vencimiento) de los flujos de caja que vencen en dichos períodos. La
expresión matemática de la duración es:
P0
xjCjVA
n=t
1=t=
VACt
n=t
1=t
xnCnVA+.....+x2C2VA+x1C1VA
=Duracion


La idea que subyace detrás de este concepto es que, a mayor duración de un título mayor será el
riesgo de que el emisor no pueda hacer frente a sus obligaciones. Si comparamos un bono que venza
dentro de cinco años con cupones anuales, con otro semejante de igual vencimiento, pero que no
pague ningún cupón hasta el último día de su vida, es decir, un bono cupón cero, veremos que,
aunque el plazo de ambos es idéntico, el bono normal un día antes de su vencimiento nos ha
entregado cuatro flujos de caja, mientras que el bono cupón cero aún no ha entregado nada. Si en
este momento la empresa emisora se declarara insolvente, habríamos perdido la totalidad de nuestra
inversión en este último, pero no todo lo invertido en el anterior. Lo que quiere decir que ambos bonos,
aún teniendo el mismo plazo, no tienen el mismo riesgo y la fecha de vencimiento no es tan definitoria
como podría parecer. Por ello, aunque el plazo de ambos bonos es idéntico, su duración no lo es.

70. 8
La variación que se produce en el precio de una obligación con respecto a una variación del 1% sobre
el rendimiento hasta el vencimiento del mismo se llama volatilidad y se mide por:
adrentabilid+1
Duración
=d(%)Volatilida
2.2.6 OBLIGACIONES CONVERTIBLES
Las obligaciones convertibles son aquellas que si el obligacionista quiere y dentro de uno o varios
plazos determinados pueden cambiarse por acciones de la entidad emisora y, a veces, por otras
obligaciones. Esto implica una ampliación de capital y el número de acciones nuevas depende del
número de obligaciones que optan por la conversión. En este caso se amortizan las obligaciones
convertibles, las obligaciones que no ejercen la opción continúan cobrando los cupones periódicos
y al vencimiento se recupera el capital.
Estas obligaciones son consideradas normalmente como capital propio diferido y los inversores
suelen acoger bien este tipo de empréstitos, sobre todo cuando se trata de empresas en crecimiento y
con buenas perspectivas.
Cuando llega el período o períodos de convertibilidad, el obligacionista pueda cambiar las obligaciones
por acciones nuevas sin que ello le suponga desembolso alguno. La valoración de estas acciones
nuevas puede ser fija o variable, dependiendo en este caso de la cotización de las acciones viejas de
la empresa en la Bolsa (normalmente se hace con un descuento prefijado sobre la cotización media de
las acciones viejas en un período inmediatamente anterior al de conversión, con o sin limite inferior de
precio), pero en todo caso debe estar estipulado en el momento de emisión de las obligaciones
convertibles.
Se denomina relación de conversión o coeficiente de conversión a la relación por cociente entre el
precio de emisión de la obligación que puede coincidir con su valor nominal y su precio de conversión
que suele ser equivalente al precio de cotización de la acción en el momento de la emisión de las
obligaciones incrementado en un determinado porcentaje, es decir:
conversióndePrecio
obligaciónladeemisióndePrecio
=conversióndeCoef.oRel.
con esta relación obtenemos el número de acciones nuevas necesarias por cada obligación
convertible.
Se llama valor de conversión de una obligación convertible al producto: Relación de conversión x
Cotización actual de la acción vieja.
Y se llama prima de conversión a la diferencia: Precio de emisión de la obligación convertible - Valor
de conversión.
El tipo de interés de las obligaciones convertibles es inferior al de las obligaciones ordinarias de las
mismas características, ya que el derecho de conversión para el propietario debe valorarse también
porque proporciona rendimientos adicionales. El valor de mercado de una obligación convertible
depende del efecto de dos factores:
a) el valor del título como mera obligación: teniendo en cuenta los cupones periódicos futuros y el
valor de reembolso actualizados a la tasa de rentabilidad exigida por el mercado.
b) el valor del mismo como opción o posibilidad de convertirse en acción. Este segundo factor
será tanto menor cuanto mayor sea la diferencia entre el precio de conversión y la cotización
actual de la acción vieja. Si el precio de conversión es muy elevado el valor de este factor será
nulo. Por otra parte, con independencia de cuál sea el precio de conversión fijado el valor de

71. 9
este segundo factor será tanto mayor cuanto mejores sean las expectativas de que el precio
de las acciones vaya a subir en el futuro.
Las obligaciones canjeables son las que incorporan el derecho de transformarse o cambiarse por
otro título: obligaciones, acciones viejas de la propia empresa o por acciones de otra empresa del
grupo. El proceso es parecido al anterior, la diferencia es que si se cambian por acciones de la
propia empresa el canje no da lugar a cambios en el capital de la empresa emisora.

72. 10
2.2.7 LA VALORACIÓN DE ACCIONES
El capital propio en una empresa que revista la forma jurídica de sociedad anónima, está constituido
por las acciones emitidas al constituirse la sociedad y por las sucesivas ampliaciones de capital que
puedan efectuarse en el tiempo. Una acción representa una parte alícuota del capital social de una
sociedad anónima. Incorpora los derechos de socio al ir unida la condición de propietario a la
titularidad de la acción y constituye una de las formas de financiación alternativa cuando la empresa
no puede o no quiere incrementar su relación de endeudamiento. Las acciones no se emiten con una
fecha prefijada de amortización, sino que su duración es ilimitada, tanto como lo haga la empresa.
Aunque pueden ser amortizada si la empresa decide reducir capital. Las acciones proporcionan a sus
propietarios los siguientes derechos:
- Participación: a percibir parte de las ganancias o bien, en el supuesto de disolución de la sociedad a
percibir la parte que le corresponda de la masa social.
- Asistencia y voto en las juntas de la sociedad: siempre que se posea el número mínimo de
acciones que prevén los estatutos para estos casos.
- Derecho preferente de suscripción: para adquirir nuevas acciones cuando la empresa amplíe su
capital.
- Transmisibilidad: o posibilidad de vender los títulos correspondientes.
Como obligaciones, tiene que desembolsar el total de su participación y su responsabilidad por las
deudas y pérdidas de la empresa, de acuerdo con su participación.
Una forma bastante usual de calcular el valor de una acción en la literatura económico-financiera
tradicional consiste en dividir el neto patrimonial (capital + reservas) de la empresa entre el número de
acciones en que se halla fraccionado el capital de la misma. Así, el valor teórico de una acción,
también llamado valor según balance, vendrá dado por:
accionesdeNumero
lpatrimoniaNeto
=accionunadeValor
El valor de una acción dado por la expresión anterior no contempla las expectativas de beneficio de la
empresa. Un inversor cuando compra una acción lo hace con la esperanza de obtener una
rentabilidad superior a la que obtendría colocando su dinero en inversiones alternativas. Un accionista
cuando arriesga su dinero comprando acciones, lo hace con la esperanza de obtener unos ingresos
futuros a través de diferentes vías: bien sea en forma de dividendos, venta de derechos de suscripción
preferentes o plusvalías de cotización realizadas en el hipotético caso de que, en un momento
posterior, logre vender en el mercado dichas acciones a un precio superior al de compra..
Más que patrimonio, el inversor compra renta, y dos empresas pertenecientes al mismo sector
productivo y con el mismo neto patrimonial pueden obtener beneficios muy distintos, debido a la
diferente política comercial, de personal, etc.
La valoración de las acciones al igual que la valoración de cualquier activo ya se trate de activos
financieros o de cualquier tipo, se obtiene a través del valor actualizado de la renta que en el futuro se
espera que genere este activo, computando dichas rentas no en la fecha del devengo sino en la que
se realizan o liquidan. Desde el punto de vista del accionista, los beneficios de la empresa se liquidan
en el momento en que son repartidos en forma de dividendos y de ahí que uno de los modelos de
valoración de acciones universalmente aceptado sea el que se basa en la actualización de los
dividendos futuros esperados, más el valor actual del precio de realización o venta que se espera
tenga la acción al final del horizonte temporal de referencia. La valoración de acciones como se ha
definido anteriormente presentan dificultad por las siguientes razones:

73. 11
a) los flujos netos de caja a percibir en el futuro se consideran como variables aleatorias con una
función de distribución subjetiva.
b) la duración de la inversión es infinita, puesto que la acción no tiene fecha de vencimiento.
c) es difícil observar la tasa de rendimiento que requiere el mercado.
2.2.7.1 Obtención de la tasa de rentabilidad de una acción
Supongamos que el precio actual de una acción es P0, que el precio esperado al cabo de un año es P1
y que el dividendo esperado por acción para dentro de un año es D1. La tasa de rentabilidad que los
inversores esperan obtener por esta acción a lo largo del próximo año será:
P0
P0-P1+
P0
D1=
P0
P0-P1+D1=r
La tasa de rentabilidad esperada de una acción, depende del (dividendo esperado/precio actual) +
(aumento esperado del precio/precio actual).
Supongamos que las acciones de la empresa X se venden hoy a 100 um. el título (P0=100), los
inversores esperan un dividendo de 5 um. (D1=5), esperan también que las acciones se vendan dentro
de un año a 110 um. (P1= 110). Entonces, la rentabilidad esperada por los accionistas será:
15%=0,15=
100
100-110+5
=r
Esta rentabilidad es la que realmente obtiene un inversor en caso de llevar a cabo la inversión a los
actuales precios de mercado.
Si tenemos las previsiones del dividendo y del precio dentro de un año, podemos obtener una
previsión del precio actual:
k)+(1
P1+D1
=P0
Donde k es la tasa de rentabilidad exigida, ajustada convenientemente a las características de riesgo
de la acción y demás circunstancias del mercado financiero. La tasa depende de la incertidumbre
asociada a los dividendos y al precio futuro de la acción, incluye una prima por riesgo que el inversor
añade al interés sin riesgo (Rf).
Los dividendos previstos por una acción de riesgo similar a la acción de la empresa X es D1=5 um. El
precio previsto para dentro de 1 año es P1=110 um. Si la rentabilidad exigida para las acciones de la
misma clase de riesgo que la empresa X es el 15%, entonces el precio actual de la acción será:
100=
1,15
110+5
=
k+1
P1+D1
=P0
¿Cómo sabemos que 100 um. es el precio real de la acción?. Porque ningún otro precio podría
perdurar en mercados de capitales competitivos. ¿Qué ocurriría sí el precio actual P0 de la empresa X
fuese superior a 100 um.? por ejemplo P0=103:
11.65%=0,11658=
103
103-5+110
=
P0
P0-D1+P1=r

74. 12
Las acciones de la empresa X ofrecerían una tasa esperada de rentabilidad que sería inferior a la
rentabilidad exigida de otros títulos de riesgo similar. Los tenedores de acciones de la empresa X
venderían éstos para comprar otros títulos de mayor rentabilidad, ocasionando en este proceso una
reducción en el precio de las acciones de la empresa X.
Si P0 fuese inferior a 100 um. (por ejemplo P0=98), el proceso sería inverso:
17.35%=0,1735=
98
985-+110
=
P0
P0-D1+P1=r
Las acciones de X ofrecerían una rentabilidad esperada mayor que los títulos comparables de igual
riesgo. En este caso los inversores comprarían acciones de X, obligando a subir el precio de las
acciones a 100 um.
La conclusión es que en cada momento todos los títulos de riesgo similar estarán valorados de modo
que ofrezcan la misma rentabilidad esperada. Esta es una condición para el equilibrio en los
mercados de capitales competitivos.
La rentabilidad exigida k es lo que demanda un inversor para realizar una inversión, mientras que la
rentabilidad esperada r es lo que realmente obtiene.
2.2.7.2 Valoración de las acciones ordinarias
El valor de mercado de una acción ordinaria viene dado por el valor actualizado de los diferentes
ingresos que espera recibir en el futuro a través de diferentes vías: dividendos, venta de derechos de
suscripción preferentes y del precio esperado de venta de la acción en un momento posterior. Ya
hemos visto como se calcula el valor actual de una acción cuando queremos mantenerla en nuestro
poder durante un período:
k)+(1
P1+D1=P0
Donde P1 dependerá de los dividendos esperados por los inversores para el año 2 y del precio
esperado al final del segundo año:
k)+(1
P2+D2
=P1
Ahora podemos expresar P0 en función de D1, D2 y P2:
)
2k+(1
P2+D2+
k)+(1
D1=
k)+(1
k)+(1
P2+D2
+
k)+(1
D1=P0
De esta forma, podemos avanzar en el futuro y llegar a una fórmula general del precio de la acción:
)
nk+(1
Pn+
k)+(1
t
Dt
n
1=t
=P0 

75. 13
En la fórmula anterior se supone, que los posibles derechos de suscripción preferente que puedan
corresponder a la acción durante los -n- años son vendidos y, por tanto, incrementan el valor del
dividendo del período o períodos correspondientes.
Las acciones no tienen vencimiento y, por tanto, no se reembolsan nunca al conjunto de los
accionistas. El período n en el que se venderían las acciones puede estar infinitamente alejado en el
tiempo, y, por tanto, el valor actual del precio de venta en el período n se aproxima a cero, y el
inversor, al calcular el precio que estaría dispuesto a pagar por las acciones, debe ignorarlo. Entonces,
la expresión para obtener el precio actual P0 sería:
k)+(1
t
Dt
1=t
=P0 

2.2.7.3 Modelos de dividendos constantes
En el caso de que los dividendos sean constantes y perpetuos en el tiempo, es decir D1 = D2 = D3....=D
tendremos que:
  k
D
=....)+
2k1
1
+
k)+(1
1
D(=P0

2.2.7.4 Modelo de crecimiento constante
Supongamos que se prevé una tendencia de crecimiento constante de los dividendos del g por uno
anual acumulativo, a partir del dividendo esperado en el año próximo D1, para calcular el precio actual
que pagaría un inversor por una acción que mantenga permanentemente en su cartera, debemos
dividir el pago por dividendo anual por la diferencia entre la tasa de descuento y la tasa de crecimiento:
g-k
D1=.......)+
)
2k+(1
g)+(1
+
k)+(1
1
(D1=....+
)
2k+(1
g)+(1D1+
k)+(1
D1=P0
Esta fórmula sólo la podemos utilizar cuando k>g ya que, si g se aproxima a k el precio de la acción
tendería a infinito.
Podemos calcular la rentabilidad exigida de la acción en una situación de crecimiento como:
g+
P0
D1=k
Donde D1/P0 es igual a la rentabilidad del dividendo y g es la tasa esperada de crecimiento.
2.2.7.5 Modelo de crecimiento no constante
Se utiliza en aquellos casos en los que la empresa:
1.- en la actualidad no está pagando dividendos, se prevé que en un determinado número de años
pagará un dividendo por primera vez y se espera que éste crecerá a una determinada tasa g de forma
indefinida. ¿Cómo obtenemos el precio de la acción hoy?.
Para ver cuál es el precio de la acción, primero se determina cuánto valdrá ésta una vez que se
paguen los dividendos. Después se puede calcular el valor actual de ese precio futuro para obtener

76. 14
así el precio actual. Si suponemos que el primer dividendo es dentro de cinco años y el dividendo
crecerá de forma constante a partir de dicho año, el precio actual lo obtenemos:
   4
k1
4P
0P
gk
5D
4P




2.- Se espera que durante los próximos tres años pague D1 , D2 y D3 en dividendos, creciendo éste
después del tercer año a una tasa constante anual g.
Como en el caso anterior, primero calculamos el valor de la acción dentro de tres años con la
expresión del modelo de crecimiento constante y, para calcular el precio actual, actualizamos el precio
dentro de tres años así como los dividendos que vamos a cobrar hasta el tercer año:
 
         3
k1
3P
3
k1
3D
2
k1
2D
k1
1D
0P
gk
g13D
3P











2.2.7.6 Obtención de la tasa de crecimiento
La tasa de crecimiento de los dividendos depende a su vez de dos factores: el crecimiento de los
beneficios y la proporción de éstos que se reparte entre los accionistas. Si ambos factores son
constantes a lo largo de los años, el dividendo también crece de manera constante. Como los precios
reflejan los beneficios y los dividendos, también los precios se suponen crecientes en el modelo de
crecimiento constante. Para calcular g vamos a utilizar el siguiente razonamiento:
Una empresa, después de haber pagado el impuesto sobre la renta de sociedades, con el beneficio
disponible puede: repartirlo todo, repartir sólo una parte, o bien, no repartir nada. Lo que reparte son
los dividendos. El beneficio disponible que no reparte (retiene) integra sus recursos propios.
Cuando la empresa es muy estable y suponemos que esta característica se seguirá manteniendo en
el futuro, cada año a los beneficios retenidos la empresa le esta ganando una rentabilidad que viene
medida por el ratio de rentabilidad del capital propio (RCP = r), que se define como:
accionesdeNumero
propiosRecursos
=*donde;
*accionporpropiocapitaldelcontableValor
BPA
=r
Supuesta una estabilidad en el futuro, la distribución del beneficio disponible será constante y el ratio
que nos mide dicha distribución es: DIV/BPA (siendo BPA el beneficio por acción). Conocido este
ratio, podemos conocer qué parte de los beneficios retiene la empresa:
b=repartodetasa-1=
BPA
DIVI
-1=retencióndeTasa
La empresa está reinvirtiendo el b% de sus beneficios que es su tasa de retención. Con estos
recursos la empresa obtiene una rentabilidad del r%, el producto br nos mide la tasa de crecimiento
del dividendo

77. 15
PROBLEMAS TEMA 2.2
PROBLEMA 2.2.1. - Una empresa emite una obligación de valor nominal 1.000 € siendo su precio
de emisión a la par y vencimiento a 10 años y el reembolso es por su valor nominal. El cupón
anual es de 80 €. Con estos datos y sabiendo que:
a) Las obligaciones de características similares tienen un rendimiento del 8%, ¿cuál sería su
precio actual? (1.000 €).
b) Ha transcurrido un año desde que se compró, si la rentabilidad de los bonos de características
similares es ahora del 10%, ¿cuál es su precio? (884,82 €).
c) Lo mismo que en el apartado b) pero suponiendo que la rentabilidad es ahora del 6%. (1.136,03
€).
PROBLEMA 2.2.2 . - Una empresa emite una obligación de valor nominal 1.000 €. y vencimiento a
7 años y el reembolso es por su valor nominal. El cupón anual es de 140 €. pero pagaderas por
semestres. Con estos datos y sabiendo que:
a) Las obligaciones de características similares tienen un rendimiento anual del 16%. ¿Cuál es su
precio actual?. (917,56 €.)
b) ¿Cuál es el rendimiento efectivo del bono?. (14.49%)
PROBLEMA 2.2.3.- Se emiten obligaciones, con las siguientes características: Co = 10.000; cupón =
12% anual; n=10 años; Cn = 10.000; k = 15%. Se pide: 1. - Precio actual de la obligación. (8.494,37)
PROBLEMA 2.2.4.- Se tienen los siguiente datos de una obligación cupón cero: Co = 10000; n=5
años; Cn=15000. Se pide:
1. - Calcular el interés nominal de la obligación. (8,447%)
PROBLEMA 2.2.5 Se tiene los siguientes datos de una obligación cupón cero: Co = 10000; cupón=
10% anual: n = 5 años. Se pide:
1. - Rentabilidad de la inversión. (10%)
PROBLEMA 2.2.6: Bono emitido a seis años con lo siguientes datos:
Co=10000; Cupón 12%; el reembolso se efectúa a la par. A los dos años suben los intereses y el
mercado exige una rentabilidad k= 12,5%. Se pide: 1. - Precio del bono a los dos años, cuando suben
los intereses. (Sol: 9.849,72 €) 2. - Supongamos que la cotización del bono es de 9.700 €. ¿cúal será
su rentabilidad? (Sol: 13,009%). Lo mismo pero con una cotización de 10.050 €. (Sol: 11,836%)
PROBLEMA 2.2.7. - Un bono del Estado de 10.000 €. de valor nominal, reparte unos cupones de 750
€. anualmente. El vencimiento es dentro de 5 años. El tipo de interés actual para emisiones libres de
riesgo a 5 años es del 10,5%. Con estos datos queremos saber: a) El precio del bono (8877,14); b) su
duración (4,3O AÑOS); c) su volatilidad (3,895%); d) si el tipo de interés desciende 50 puntos básicos
en los próximos días, cuál será su ganancia de capital (175,16 €.).
PROBLEMA 2.2.8. - Dos obligaciones presentan los siguientes flujos de caja:
P0 1 2 3 4 5
A
B
- 852,1
-1054,3
50
100
50
100
50
100
50
100
1050
1100
Se pide calcular la rentabilidad, la duración y la volatilidad de ambas obligaciones.
Obligación A: 8.781%; 4,502 años; 4,139%
Obligación B: 8,618%; 4,193 años; 3,86%
PROBLEMA 2.2.9. - Un inversor quiere comprar un bono con cupón del 12% a tres años, de 10.000 €.
de nominal. El tipo de interés de mercado para ese nivel de riesgo y plazo es del 14%. El bono acaba

78. 16
de cortar cupón. Se pide: a) Cuál es el precio que debería pagar por dicho bono?.(9535.67) b) ¿Cuál
es la duración del bono?.(2,682 años) c) ¿Cómo variará el precio del bono sí los tipos de interés:
c.1) bajan al 12% (+464,33 €)
c.2) suben al 15% (-220,64 €)
PROBLEMA 2.2.10 - Calcular el precio de un bono el 1.11.12 que presenta las siguientes
características:
a) valor nominal = 10.000 €. b) cupón 7% anual pagadero el 31 de diciembre de cada año. c)
vencimiento del bono 31.12.2016 d) rentabilidad actual para bonos similares el 8,5%. (Precio total
31/12/12 = 10.208,06; Precio total 01/11/12 = 10.071,92; CC = 583,33 ; Precio del bono01/11/12 = 9.488,58)
PROBLEMA 2.2.11 - Un bono de 1.000 €. de valor nominal, vence dentro de tres años. Abona
cupones semestrales de 50 €. y su valor de reembolso es de 1.050 €. ¿Cuál es su rentabilidad?,
(11.771%)
PROBLEMA 2.2.12. - Una empresa paga un dividendo por acción de 100 €. año. Si esta política
continúa de forma perpetua, ¿cuál es el valor de una acción si el rendimiento exigido es del 20%?.
(500 €.).
PROBLEMA 2.2.13. - Una empresa espera paga el año próximo un dividendo de 40 €. por acción.
Los inversionistas exigen un rendimiento del 16% para las acciones de la empresa. Si el dividendo
se espera que aumente un 6% acumulativo anual. Se pide:
a) Precio actual de la acción. (400 €.)
b) ¿Cuál será su precio dentro de cuatro años?. (505 €.)
PROBLEMA 2.2.14. - Una empresa no está pagando dividendos en la actualidad. Se prevé que en
cinco años pagará dividendos por primera vez. Este dividendo será de 50 €. por acción y se espera
que crecerá al 10% acumulativo anual de forma indefinida. Los inversionistas exigen una
rentabilidad del 20%. Se pide:
a) Precio de la acción dentro de cuatro años. ( 500 €)
b) El precio de la acción hoy. (241,12 €.)
PROBLEMA 2.2.15. - Una empresa prevé los siguientes dividendos para los próximos años:
Año Dividendo
1
2
3
100
200
250
Después del tercer año, el dividendo crecerá a una tasa constante del 5% anual. El rendimiento
exigido a esta empresa por los inversionistas es del 10% :
 Precio de la acción en el año 3. ( 5.250€)
 ¿Qué vale la acción hoy?. (Sol: 4.388,42 €.).
PROBLEMA 2.2.16 - Un inversionista compra una acción de una empresa que tuvo el año anterior un
beneficio por acción de 350 €. y repartió un dividendo de 190 €./acción. La tasa de crecimiento del
dividendo y del beneficio durante los últimos años ha sido, por término medio, de un 5% anual, se
espera que, dicha tasa de crecimiento continúe en el futuro. Si la rentabilidad exigida para dicha
empresa es del 12%. Se pide:
a) Precio de la acción. (Sol: 2.850 €.)
c) Si en el mercado la acción está a 4.000 €. ¿cuál es la rentabilidad esperada?. (Sol: 9,99%)
PROBLEMA 2.2.17.- Suponga que ha adquirido a finales de 2012 bonos con un valor nominal de
10.000 um. que tienen un cupón del 10% pagadero anualmente por períodos vencidos y con
vencimiento a los 5 años. Se pide:

79. 17
a) Suponiendo que el interés del mercado es del 10%, calcular el importe que habrá pagado por
estos bonos. (10.000€)
b) ¿Cuál debería ser el valor de mercado de los títulos suponiendo que el tipo de interés del
mercado suba un punto? ¿Y si baja un punto? Comentar los resultados obtenidos. (9.630,41€;
10.388,97€)
c) Suponga que existe otro bono con el mismo nominal, vencimiento y un cupón del 9,5%
pagadero anualmente. Calcule el valor de mercado de este bono para k=10%, al 11% y por
último para k=9%. Comente las distintas variaciones de este bono respecto al anterior.
(9.810,46; 9.445,62€; 10.194,48€)
PROBLEMA 2.2.18 Sea un bono con nominal de 10000 u.m., vencimiento 3 años, cupón del
10,25% anual pagadero por trimestres vencidos. El tipo de interés del mercado es del 9,75% anual
pagadero trimestralmente.
a) Obtenga la duración y la sensibilidad a las variaciones en los tipos de interés. (10.493 trimestres;
2.3822%)
b) Suponga otro bono con idénticas características excepto el cupón que es del 12% anual
pagadero trimestralmente. ¿Será la sensibilidad a las variaciones en los tipos de interés de este
segundo bono mayor o menor que la del primero? Razone la respuesta. (Sensibilidad: 2.3408%)
c) Si ahora el interés del mercado es del 11% anual, ¿qué pasaría con la duración del primer bono?
¿Y con su precio? (10.463 trimestres; 9.810,55€)