Potencial eléctrico desde un cable DC
•
1 recomendación•143 vistas
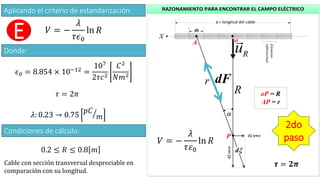
El documento describe cómo calcular el potencial eléctrico en un punto a distancia R de un cable de cobre que transporta una corriente continua. Explica que el potencial eléctrico V en un punto está dado por la ecuación V = -λ/(τε0)lnR, donde λ es la densidad de carga en el cable, τ es 2π, y ε0 es la permitividad del vacío. Luego, el documento presenta un diagrama de flujo y código MATLAB para simular numéricamente el potencial eléctrico en función de la distancia
Recomendados
Más contenido relacionado
La actualidad más candente
La actualidad más candente (19)
Destacado
Destacado (16)
Similar a Potencial eléctrico desde un cable DC
Similar a Potencial eléctrico desde un cable DC (20)
Último
Último (20)
Potencial eléctrico desde un cable DC
- 1. Potencial eléctrico en un punto desde en un cable de cobre de DC Codificación (simulación) en MATLAB Por José Sanabria García, BOLIVIA
- 2. En un cable que porta una densidad de carga l: ¿Cómo varia el potencial eléctrico con la distancia? RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal Modelo: Ley de Coulomb Herramienta: Cálculo infinitesimal 1er paso
- 3. Si en el punto “P” hubiera una carga “q0”, y si en el punto “A” hubiera una carga infinitesimal “dq”. ¿Cuál es la fuerza infinitesimal que experimentarían esas cargas? RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal 𝑑𝐹 = 𝐾𝑒 𝑞0 𝑑𝑞 𝑟2 𝑲 𝒆 = 𝟏 𝟐𝝉𝝐 𝟎 dF 𝝐 𝟎 = 𝟖. 𝟖𝟓𝟒 × 𝟏𝟎−𝟏𝟐 = 𝟏𝟎 𝟕 𝟐𝝉𝒄 𝟐 𝑪 𝟐 𝑵𝒎 𝟐 Modelo: Ley de Coulomb Herramienta: Cálculo infinitesimal 𝝉 = 𝟐𝝅
- 4. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal 𝑑𝐹 = 𝐾𝑒 𝑞0 𝑑𝑞 𝑟2 Por otra parte sabemos que el campo eléctrico infinitesimal en el punto “P” (donde está la carga “q0”) es igual a: 𝑑𝜉 = 𝑑𝐹 𝑞0 = 𝐾𝑒 𝑑𝑞 𝑟2 = 𝑑𝑞 2𝜏𝜖0 𝑟2 dF En nuestro caso dq = lds, por lo tanto: 𝑑𝜉 = 𝜆𝑑𝑠 2𝜏𝜖0 𝑟2 Este campo está dirigido según la línea AP. La fuerza infinitesimal “dF” que experimentarán las cargas “q0” y “dq” estará dada por la ley de Coulomb:
- 5. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝑑𝜉 = 𝜆𝑑𝑠 2𝜏𝜖0 𝑟2 Debido a la simetría del problema, a cada elemento “ds”, situado a la distancia “s” a la izquierda del punto “o” corresponde otro elemento infinitesimal “ds” a la misma distancia “s” a la derecha del punto “o”: Por lo tanto los componentes horizontales del campo eléctrico se anularán, esto es: 𝜉 𝑥 = න 𝑠→−∞ +∞ 𝑑𝜉 𝑥 . = න 𝑠→−∞ +∞ 𝑑𝜉 sin 𝛼 = 0 P + - +𝑑𝜉 sin 𝛼 −𝑑𝜉 sin 𝛼
- 6. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝑑𝜉 = 𝜆𝑑𝑠 2𝜏𝜖0 𝑟2 En cambio las componentes verticales del campo eléctrico darán la misma contribución en ambas partes del cable: 𝜉 𝑦 = න 𝑠→−∞ +∞ 𝑑𝜉 𝑦 . = න 𝑠→−∞ +∞ 2𝑑𝜉 cos 𝛼 P - + +𝑑𝜉 co𝑠 𝛼 +𝑑𝜉 cos 𝛼
- 7. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝑑𝜉 = 𝜆𝑑𝑠 2𝜏𝜖0 𝑟2 Por lo tanto el campo eléctrico total en el punto P producido por la circulación de un corriente continua de densidad lineal l será expresado por la siguiente ecuación: 𝜉 = 2 න 𝛼=0 +𝜏/4 𝑑𝜉 cos 𝛼 𝝉 = 𝟐𝝅 Del gráfico obtenemos: cos 𝛼 = 𝑅 𝑟 Es decir: 𝑟 = 𝑅 cos 𝛼 = 𝑅 sec 𝛼 A
- 8. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝑑𝜉 = 𝜆𝑑𝑠 2𝜏𝜖0 𝑟2 𝝉 = 𝟐𝝅 Asimismo establecemos que: tan 𝛼 = 𝑠 𝑅 Es decir: 𝑠 = 𝑅 tan 𝛼 Por lo tanto: 𝑑𝑠 = 𝑅 𝑠𝑒𝑐2 𝛼 𝑑𝛼 B Sustituyendo las expresiones A y B en C: C 𝑑𝜉 = 𝜆𝑅 𝑠𝑒𝑐2 𝛼 𝑑𝛼 2𝜏𝜖0 𝑅 sec 𝛼 2 = 𝜆𝑑𝛼 2𝜏𝜖0 𝑅
- 9. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝑑𝜉 = 𝜆𝑑𝑠 2𝜏𝜖0 𝑟2 𝝉 = 𝟐𝝅 Por lo tanto el campo eléctrico total será: 𝜉 = 2 න 𝛼=0 𝜏/4 𝑑𝜉 cos 𝛼 = 2 න 𝛼=0 𝜏/4 𝜆𝑑𝛼 2𝜏𝜖0 𝑅 cos 𝛼 Simplificando: 𝜉 = 𝜆 𝜏𝜖0 𝑅 න 𝛼=0 𝜏/4 cos 𝛼𝑑𝛼 Resolviendo y destacando el vector: Ԧ𝜉 = 𝜆 𝜏𝜖0 𝑅 𝑢 𝑅
- 10. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝝉 = 𝟐𝝅 Obtenido el campo eléctrico total en el punto P, recordamos que: Ԧ𝜉 = 𝜆 𝜏𝜖0 𝑅 𝑢 𝑅 D Ԧ𝜉 = −𝛻𝑉 = −𝑔𝑟𝑎𝑑(𝑉) V es el potencial eléctrico [J/C] o [V]. Este gradiente de potencial podemos expresar: Ԧ𝜉 = − 𝜕𝑉 𝜕𝑥 𝑢 𝑥 + 𝜕𝑉 𝜕𝑦 𝑢 𝑦 + 𝜕𝑉 𝜕𝑧 𝑢 𝑧 En nuestro caso sólo hay una dirección vectorial, la que corresponde a R: Ԧ𝜉 = − 𝜕𝑉 𝜕𝑅 𝑢 𝑅 = − 𝑑𝑉 𝑑𝑅 𝑢 𝑅 Observe que la derivada parcial se convierte a derivada total ya que solo hay una dirección vectorial.
- 11. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝝉 = 𝟐𝝅 Igualando la gradiente a la ecuación D: Ԧ𝜉 = −𝛻𝑉 = − 𝑑𝑉 𝑑𝑅 𝑢 𝑅 = 𝜆 𝜏𝜖0 𝑅 𝑢 𝑅 Simplificando: Consideraremos que para R0 = 1 m el potencial V es “cero” (0 voltios) con propósitos de estandarización. 𝑑𝑉 = − 𝜆 𝜏𝜖0 𝑑𝑅 𝑅 𝑑𝑉 = 𝜆 𝜏𝜖0 𝑑𝑅 𝑅 න 𝑉=0 𝑉 𝑑𝑉 = − 𝜆 𝜏𝜖0 න 𝑅=𝑅0 𝑅 𝑑𝑅 𝑅 Resolviendo: 𝑉 = − 𝜆 𝜏𝜖0 ln 𝑅 − ln 𝑅0
- 12. RAZONAMIENTO PARA ENCONTRAR EL CAMPO ELÉCTRICO Ru s = longitud del cable ds r R oA P d a d sena dcosa X oP = R AP = r Elemento infinitesimal dF 𝝉 = 𝟐𝝅 Aplicando el criterio de estandarización: 𝑉 = − 𝜆 𝜏𝜖0 ln 𝑅 𝑉 = − 𝜆 𝜏𝜀0 ln 𝑅 𝜖0 = 8.854 × 10−12 = 107 2𝜏𝑐2 𝐶2 𝑁𝑚2 Donde: 𝜏 = 2𝜋 𝜆: 0.23 → 0.75 ൗ𝑝𝐶 𝑚 Condiciones de cálculo: 0.2 ≤ 𝑅 ≤ 0.8 𝑚 Cable con sección transversal despreciable en comparación con su longitud. 2do paso E
- 13. Ecuación deducida: 𝑉 = − 𝜆 𝜏𝜖0 ln 𝑅 𝜖0 = 8.854 × 10−12 = 107 2𝜏𝑐2 𝐶2 𝑁𝑚2 Donde: 𝜏 = 2𝜋 𝜆: 0.23 → 0.75 ൗ𝑝𝐶 𝑚 Condiciones de cálculo: 0.2 ≤ 𝑅 ≤ 0.8 𝑚 Cable con sección transversal despreciable en comparación con su longitud. E DIAGRAMADEFLUJOPARAELPOTENCIALELECTRICO tau = 2p 0.23 ≤ L ≤ 0.75 x 10-12 ? Lmin = 0.23 x 10-12 e0 = 1 x 107 /(2*tau*c2 ) si Lmax = 0.75 x 10-12 L INICIO no dR = 0.01 0.2 ≤ R ≤ 0.8 V = -L*ln(R)/(tau*e0) Gráfico FINAL 2do paso E
- 14. DIAGRAMADEFLUJOPARAELPOTENCIALELECTRICO tau = 2p 0.23 ≤ L ≤ 0.75 x 10-12 ? Lmin = 0.23 x 10-12 e0 = 1 x 107 /(2*tau*c2 ) si Lmax = 0.75 x 10-12 L INICIO no dR = 0.01 0.2 ≤ R ≤ 0.8 V = -L*ln(R)/(tau*e0) Gráfico FINAL 2do paso E % pe00.m Programa de simulación del potencial eléctrico en un punto % localizado a una distancia R de un cable de cobre delgado que trasporta % corriente continua con una densidad constante en C/m. clearvars; close all; clc; c = 299792458; tau = 2*pi; e0 = 1e7/(2*tau*c^2); Lmin = 0.23e-12; Lmax = 0.75e-12; s = 'Introduzca la densidad lineal de carga L = '; L = input(s); if L <= 0.23e-12 || L >= 0.75e-12 disp('ERROR: 0.23 <= L >=0.75 pC/m!'); Ldat = (Lmin+Lmax)/2; else Ldat = L; end 3er paso
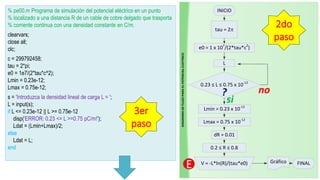
- 15. DIAGRAMADEFLUJOPARAELPOTENCIALELECTRICO tau = 2p 0.23 ≤ L ≤ 0.75 x 10-12 ? Lmin = 0.23 x 10-12 e0 = 1 x 107 /(2*tau*c2 ) si Lmax = 0.75 x 10-12 L INICIO no dR = 0.01 0.2 ≤ R ≤ 0.8 V = -L*ln(R)/(tau*e0) Gráfico FINAL 2do paso E dR = 0.01; R = 0.2:dR:0.8; Vmin = -Lmin*log(R)/(tau*e0); Vmax = -Lmax*log(R)/(tau*e0); Vdat = -Ldat*log(R)/(tau*e0); Vm = ceil(max(1e3*[Vmin, Vmax, Vdat])); % SALIDA DE GRAFICOS plot(R,1e3*Vmin,R,1e3*Vmax,R,1e3*Vdat); vs = [0.2,0.8,0,Vm]; axis(vs); grid on; s1 = 'Potencial eléctrico para lambda = 0.23 pC/m'; s2 = 'Potencial eléctrico para lambda = 0.75 pC/m'; s3 = num2str(Ldat*1e12); s4 = strcat('Potencial eléctrico para lambda = ',s3,' pC/m'); title('Variación del potencial eléctrico en un cable delgado'); xlabel('R, metros'); ylabel('Potencial Eléctrico, mV'); legend(s1, s2, s4); 3er paso E
- 16. E 4to paso ¿Cómo varia el potencial eléctrico con la distancia?: Presentación de resultados
- 17. Potencial eléctrico en un punto desde en un cable de cobre de DC GRACIAS Bolivia, 2016